問題PDF
1から10まで、それぞれの番号がかかれた玉が1個ずつ、全部で10個あります。10個の玉はA、Bどちらかの箱に入っていて、サイコロを振るごとに、「1」から「6」のうちの出た目の数で割り切れる番号のかかれた玉を移しかえます。
例えば、はじめに全部の玉がAに入っていて、サイコロを振って「2」の目が出たとします。そのときは、2、4、6、8、10の玉をBへ移します。その後、またサイコロを振って「3」の目が出たとします。そのときは、3、9の玉をBへ移し、6の玉をAへ移すので、Aには1、5、6、7の玉、Bには2、3、4、8、9、10の玉が入っていることになります。
(1)
はじめに全部の玉がAに入っていて、サイコロを3回振って「4」、「1」、「5」の目が出ました。Aに入っている玉の番号を小さい順にすべて答えなさい。
(2)
全部の玉がAに入った状態からサイコロを何回振っても、ある番号とある番号の玉は必ず同じ箱に入っています。その番号の組をすべて答えなさい。例えば、1と2の組を答える場合は、(1、2)のように書きなさい。
(3)
はじめに全部の玉がAに入っていて、サイコロを4回振って玉を移しかえました。その結果、Aに6個、Bに4個の玉が入っていました。出た目は4回ともすべて異なり、Aには1と10の玉が入っていることがわかりました。Aに入っている玉の番号を小さい順にすべて答えなさい。ただし、1と10は解答欄にすでに書いてあるので、それ以外の番号を答えなさい。
@解説@
以下、サイコロの出目を【 】で示す。
(1)
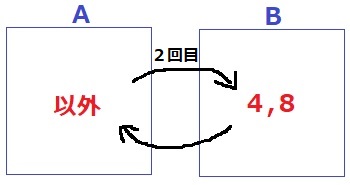
1回目は4、8がBに移動。
2回目の【1】で左右が入れ替わる。
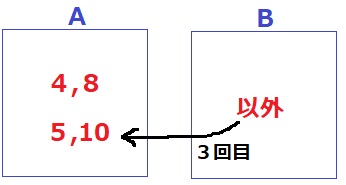
3回目は5、10がBからくる。
Aに入っている玉は4、5、8、10。
(2)
1~10を÷1~6をして割り切れる数でふるい分けたい。
割り切れる数といえば…約数
各々の約数のうち、6以下をピックアップする。
1→【1】
2→【1・2】
3→【1・3】
4→【1・2・4】
5→【1・5】
6→【1・2・3・6】
7→【1】
8→【1・2・4】
9→【1・3】
10→【1・2・5】
共通の出目だけを持つもの同士は運命共同体。
(1、7)(3、9)(4、8)
(3)
~条件~
●4回の出目はすべて異なる。
●4回目後、Aには1と10の玉を含む6個、Bには4個の玉があった。
1を動かすには、サイコロで【1】を出すしかない。
1がAに残っているということは、【1】は出さない。
10がAに残っている→10はAB間を0往復(まったく動かない)か1往復か2往復した。
◆10が2往復する
10が4回すべて動くことになるが、10は【1・2・5】しか動かないから無理。
◆10が0往復する
10がずっとAに居つづけるには【3・4・6】を出すしかない。
サイコロを4回振ったら、10は必ず動く。×
ということは、10は1往復する。
→【1】は出せないので、出目の2回は【2・5】が確定する。

AとBが5個ずつになる。ここからAだけに注目する。
最終的にAは6個になるので、残りの出目2回でAの数を+1したい。
Aの数の変化を調べると、【3】…-1個、【4】…+2個、【6】…+1個。
【3】と【4】を出せばAは+1されて数が6個になる。
【3】を出してAから3、9が去り、6が追加。
【4】を出してAに4、8が追加。
答えは1と10以外なので、4、6、7、8



コメント