問題PDF
正方形の折り紙を点線にそって折っていき、はさみでまっすぐ切ります。
切ったあとに広げると、折り方と切り方によってさまざまな形ができます。
例えば、正方形を下図のように3回折り三角形ABCをつくります。

三角形ABCを下のように赤い線にそってはさみで切ると、正方形の枠のような形になります。
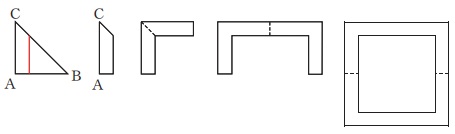
このように正方形を何回か折ってはさみで切ることを考えるとき、次の問いに答えなさい。
(問1)
例と同じようにおいた三角形ABCに、頂点Aから辺BCと垂直になるよう引いた赤い線をかきます。
それにそって切ったときにできる図形のうち、頂点Bをふくむ方の図形は何か答えなさい。
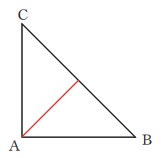
(問2)
例と同じようにおいた三角形ABCを1回だけまっすぐ切り、頂点Bをふくむ方の図形を正八角形とすることを考えます。図の頂点Aからはさみを入れるとき、辺BC上のどこを通るように切れば正八角形になるか説明しなさい。

(問3)
下図のように2回折った後、3等分してから切ることを考えます。

下図のように赤い線をひき、それにそってはさみで切るとき、
(あ)を含む図形はどのような形になりますか。
解答らんにある図を利用してコンパスと定規を用いてかきなさい。
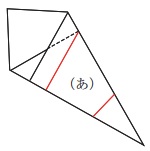

@解説@
(問1)
折り目を対称の軸として対称移動させていく。
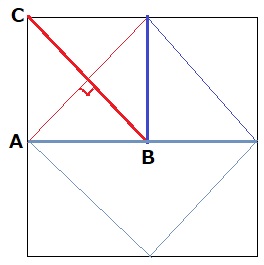
正方形になる。
(問2)
結果が正八角形になるように切る。
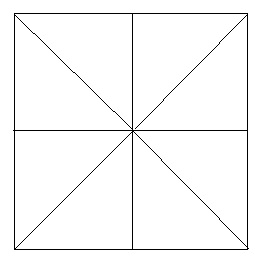
先に紙の折り目だけ広げてみよう。
中心角がちょうど8等分になる。
それぞれに正八角形の8等分の1を作成する。

頂角が45°の二等辺が8つ円形に並ぶ。
辺BC上において、BからABと同じ長さになる場所を通るようにハサミを入れればいい。
(問3)
コンパスと定規で作図する。
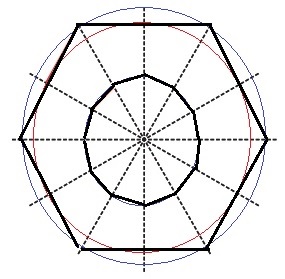
折り目に対して対称移動させる。外側は半径の長さが異なる点に注意!
コンパスで半径をとってグルっと回す。外は正六角形、中は正十二角形となる。
*実際にやってみよう!



コメント