問題ＰＤＦ
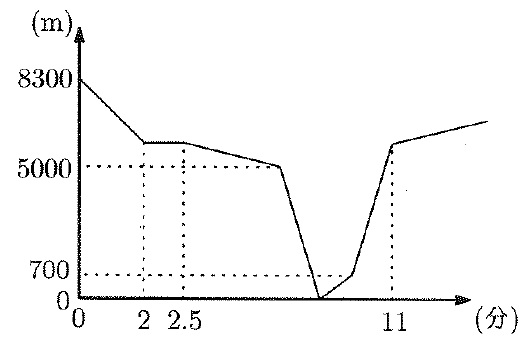
Ａ駅を出発しＢ駅、Ｃ駅、Ｄ駅の順に各駅に停車する普通列車と、Ｄ駅を出発しＣ駅、Ｂ駅には停車せず、Ａ駅に停車する急行列車があります。この日普通列車はＡ駅を午前８時に出発し、1800ｍを走り切りＢ駅に到着しました。混雑の影響でＢ駅からＤ駅まではＢ駅に到着するまでの２/３倍の速さで運行することになりました。普通列車がＢ駅を出発した何分か後に急行列車がＤ駅を出発し、普通列車がＣ駅に停車した瞬間に急行列車がＣ駅にさしかかり２台の列車の先頭がちょうど重なりました。そして、普通列車はＣ駅で、Ｂ駅に停車時間と同じ時間だけ停車してＣ駅を出発しました。その後、急行列車はＡ駅に到着し、運転間隔の調整のため、しばらく停車しました。下のグラフは普通列車がＤ駅に到着する手前までの様子を表したもので、縦の軸は普通列車の先頭から急行列車の先頭までの距離を表し、横の軸は普通列車が出発してからの時間を表します。次の各問いに答えなさい。ただし、普通列車と急行列車の先頭から最後尾までの車両の長さは同じであり、駅から出発するときの加速と、到着するときの減速は考えないものとします。
（１）
急行列車の速さは分速何ｍですか。
（２）
普通列車がＢ駅を出発してＣ駅に到着するまでに走った距離は何ｍですか。
（３）
普通列車がＤ駅に到着した時刻を求めなさい。
＠解説＠
本文だけで476文字ありました(´ﾟдﾟ｀)
（１）
グラフの意味は正確に！ここをミスると全て落とす。
普通と急行の距離が5000ｍになったあと、両者は急激に接近している。
普通はＢ～Ｃ駅間を走っており、グラフが急になるところで急行が出発したことになる。
縦軸が０のときに両者は出会い、そのとき、普通はＣ駅に停車。
ということは、緩やかに離れているところは急行のみ走っている。
普通がＣ駅を出てグッと距離が離れていき、11分で急行はＡに到着する。
普通がＣ駅に停車した時間はＢ駅の停車時間と同じ。
2.5－２＝0.5分間
急行の速さは、700ｍ÷0.5分＝分速1400ｍ
（２）
処理能力が試される。
普通は、Ａ～Ｂ間1800ｍを２分間で走る。
1800ｍ÷２分＝分速900ｍ
しかし、Ｂ駅発車後は２/３倍になるので、以降は分速600ｍで走る。
Ｂ駅～急行出発までに、普通は8300ｍ－5000ｍ－1800ｍ＝1500ｍ走る。
1500ｍ÷分速600ｍ＝2.5分間
急行出発は５分となる。
普通と急行は5000ｍ離れており、１分あたり1400＋600＝2000ｍ近づく。
5000÷2000＝2.5分後に両者は出会う。つまり、7.5分のところ。
同時に普通はＣ駅に到着した。
普通がＢ出発～Ｃ到着までに走った時間は、2.5＋2.5＝５分間
その距離は、分速600ｍ×５分＝3000ｍ
（３）
急行が走ったところに着目しよう。
急行は途中停車せずにＤからＡ駅に向かう。
分速1400ｍ×６分＝8400ｍを走る。
ここで、グラフの縦軸が8300ｍしかない点との整合性を確認。
グラフの8300ｍは普通の先頭と急行の先頭の距離。
Ａ駅とＤ駅のホームで、互いに近いほうの端～端までの距離。
急行列車がＤ駅から出発するとき、列車の先頭はＡ駅側のＤ駅のホームの先端にあるが、
Ａ駅に到着したときは急行の車両がすべてＡ駅におさまったとき、
すなわち、Ｄ駅側のＡ駅のホームの先端に車両の最後尾が入ったとき。
→急行が実際に走った距離は、Ａ～Ｄ駅間の距離に加え、車両の長さを足した距離となる。
急行の車両の長さは、8400ｍ－8300ｍ＝100ｍ
普通の車両の長さも同じく100ｍ。
普通のＢ駅発車～Ｄ駅到着を考える。
（6500ｍ＋100ｍ）÷分速600＝11分間
Ｂ駅とＣ駅での停車時間は、0.5分×２＝１分間
Ａ駅出発～Ｂ到着までは２分なので、
11＋１＋２＝14分
普通のＡ駅出発は午前８時だから、Ｄ駅到着時刻は午前８時14分となる。
キツイね(;`ω´)
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント