2023年度　豊島岡女子学園中学２回目過去問【算数】大問６解説

問題ＰＤＦ
下の図のように、１辺の長さが８ｃｍの立方体ＡＢＣＤ―ＥＦＧＨがあり、
辺ＦＧの真ん中の点をＭとします。正方形ＢＦＧＣの内部に直線ＭＰの長さが１ｃｍ、
角ＰＭＦの大きさが90度となるように点Ｐをとります。このとき、次の各問いに答えなさい。
（１）
辺ＤＨ上にＤＱの長さが２ｃｍとなるように点Ｑをとります。
３点Ａ、Ｐ、Ｑを通る平面と辺ＦＢが交わる点をＩとするとき、ＦＩの長さは何ｃｍですか。 

（２）
点Ｒは辺ＣＤ上の点です。３点Ａ、Ｐ、Ｒを通る平面でこの立方体を切ったところ、
切り口の形が五角形になりました。このとき、ＤＲの長さは〔　　〕より長くなります。
〔　　〕にあてはまる数のうち最も小さい数を答えなさい。

（３）
下の図は正方形ＣＧＨＤを１辺の長さが１ｃｍの正方形に分割したものであり、
●はその正方形の頂点です。点Ｓは 下の図の ● のいずれかの点です。
３点Ａ、Ｐ、Ｓを 通る平面でこの立方体を切ったところ、切り口の形が五角形になりました。
このとき、●で示した81個の点のうち、点Ｓの位置としてふさわしいものは何個ありますか。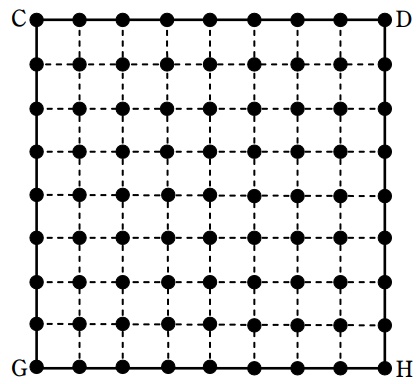

＠解説＠
（１）

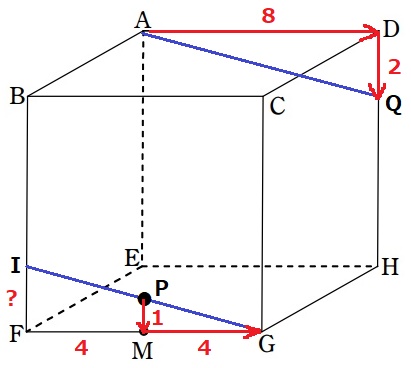
Ａ→Ｄ→Ｑは右に８、下に２の勾配こうばい。（逆にいえば下に２、右に８）

（２）

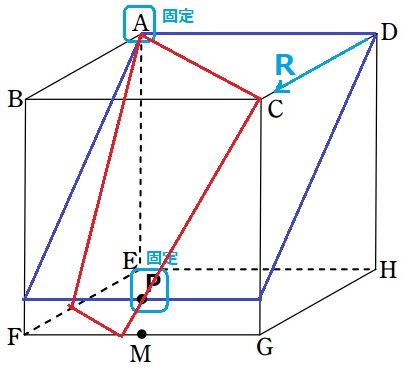
ＲがＤからＣに向かう。
スタートのＤでの切断面は青枠の四角形。
途中で五角形に切り替わるタイミングがあり、ゴールのＣでは赤枠の四角形に戻る。
固定点はＡとＰ。スタートのＤから考えると、距離が遠いＰ側の動きが把握しづらい…。

そこで、ゴールのＣから遡さかのぼると、ちょっと戻るだけで面ＣＧＨＤ上に三角形ができることで、
頂点の数が１個増えて切断面は五角形になる。
ＣＧ上の点をＪ、ＦＧ上の点をＫとして、ゴール時のＣから逆再生してＪＫの動きを追うと、
ＪはＣから下がってＪＰの傾きが緩やかになり、その延長にあるＫは左方向に動く。

ＥＦ上の点Ｌを見てみると、ＡＲとＬＫは平行でＡＲがＡＤに接近することから、
ＬはＫと同様にＦ方向に動いている。
外側に延長した切断面が隆起してＦに交われば、ＫとＬはＦで一致する。
→頂点が１個減って切断面が四角形になる。

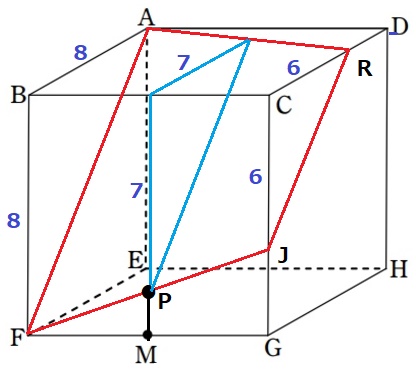
△ＡＢＦは等辺８ｃｍの直角二等辺三角形。
中間が等辺７ｃｍなので、△ＲＣＪは等辺６ｃｍの直角二等辺。
ＤＲ＝８－６＝２ｃｍ

（３）

前問でＤＲ＝２ｃｍを超えた瞬間に、切断面が四角形から五角形になった。
左上図のＲＪより左側にＳがあると五角形になる。
しかし、ＲがＣにあるときは四角形だったので、Ｃは除外する。

Ｒの動きから正方形ＣＧＨＤの左上がわかったので、
今度は残りの右下について、（１）のＱをＨ方向に動かして調べる。
ＤＱ＝２ｃｍを超えると切断面の頂点Ｇから頂点が２つに分かれて五角形になる。
→ＱＧより右にＳがあると五角形。

ＲがＣにあるときに四角形だったので、ＱがＨにあるときを調べると同様に四角形である点に注意！
切断面が立方体の頂点に交わると、２つの頂点が統合されて頂点の数が１個減る。

直線上の点は含まない。該当するＳの位置は20＋29＝49個
難関中（算数科）解説ページに戻る