問題PDF
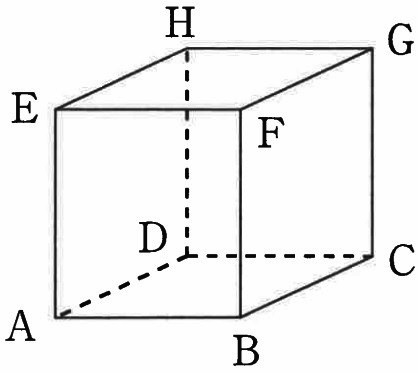
立方体の各頂点に図のようにAからHまで名前をつけます。
以下の問いに答えなさい。
必要ならば、角すいの体積は(底面積)×(高さ)÷3で求められることは使ってもかまいません。
(1)
すべての面について対角線の交点をとります。
この6つの点を頂点とする立体の体積は、立方体の体積の何倍になりますか。
(2)
4点A、C、F、Hを頂点とする立体の体積は、立方体の体積の何倍になりますか。
この立方体を、ある直線を軸として回転させます。1回転するあいだに立方体が同じ形に重なる回数を、その直線の位数と呼ぶことにします。なお、1回転してはじめて最初の形に重なるときの位数は1とします。
(3)
立方体の内部を通過する直線のうち位数が2、3、4となる例を考え、
それぞれの直線が立方体と交わる2点はどのような点であるか答えなさい。

(4)
位数が5以上の直線はないことを説明しなさい。
@解説@
(1)

正八面体。
2つの四角錐が上下にくっついた立体と考える。
上からながめると、四角錐の底面積は正方形の1/2倍。
2つの四角錐の高さの合計は正方形の高さ。
角錐の体積は(底面積)×(高さ)÷3だから、
底面積×高さ÷3=1/2×1×1/3=1/6倍
(2)

↑このような四面体になる。
立方体から4つの三角錐を引けばいい。
立方体の体積を1とすると、1つの三角錐の底面積は1/2倍、錐で1/3倍だから1/6。
1-1/6×4=1/3倍
@別解@

HFの中点をIとする。
面AICは底面の正方形ABCDに対して垂直であり、
面AICに対してFBとHDは平行である。
三角錐F—AICの頂点FをBに、三角錐H—AICの頂点HをDに等積変形すると、
右の図のように四角錐I—ABCDに変形できる。
錐は柱(立方体)の1/3だから1/3倍。
(3)
なかなか面白い問題です。
どこかに軸を設定して立方体を1回転させたとき、
スタート時点の立方体とピタッと重なる回数が位数になる。
位数が2であれば、1回転で2回重なる。
こういう問題は変なところに軸はない。
頂点や辺の中点、面の中心などを軸が通過しないと、
立方体を回転させたときに立方体がピタっとはまらず、位数1になる。
ポイントは立体ではなく、先に軸方向から立方体を見た平面で考えること!
そして、対称性を意識する。
平面を回転移動させたときに同じ形になれば位数が増える。
◆位数2

1回転で2回重なるということは180°の回転でピタッと重なる図形、すなわち点対称。
上の図では長方形ABGHに狙いを定めた。
(例)EFの中点とCDの中点を通る直線
*他にも長方形があるので、解答は複数ある。
◆位数3

1回転で3回重なる→120°ずつで重なる→正三角形!
正三角形EGBと正三角形HCAを組み合わせて考えると、
対角線DFの延長線上から立方体をながめると正六角形に見える。
正六角形だと60°ずつの回転で重なりそうに思えるが、
立体で捉えなおすとE・G・BとH・C・Aは重ならない(H・C・Aは奥を回る)
位数は6ではなく3である。
(例)立方体の対角線DFを通る直線
◆位数4

仕組みさえわかれば、すぐ出てくる、
1回転で4回重なる→90°ずつで重なる→正方形。
(例)正方形ABCDの対角線の交点と正方形EFGHの対角線の交点を通る直線
(4)
本校恒例の説明問題。
(3)がわかってもすんごく書きづらい(´゚ω゚`;)

立方体は6つの面、8つの頂点、12本の辺で構成される。
立方体をクルクル回して初期状態にピタッと重なる瞬間を見極めるには、
頂点の位置を把握するのがベストである。
なぜなら、辺の端が頂点であり、面が集まるのも頂点だから、
立方体の端っこである頂点が3次元の空間で同じ位置にくれば、
立方体全体が同じ位置にピタッと重なったといえるから。
位数が5の場合、72°の回転で図形が重なるので正五角形や星型が挙げられるが、
最低でも頂点が5個以上でなければならない。
(3)では、軸に対して垂直な平面の形に着目した。
『軸に対して垂直な平面(立方体の断面)をみたとき、
立方体の頂点がその平面に5個以上なければ位数が5以上にならない。
しかし、そのような平面がないので、位数が5以上にならない』
@回転対称@
図形を回転移動させたとき、元の状態と重なることを回転対称という。

横浜翠嵐高校で出題されました。問2です。
位数という言葉が初耳で元ネタを調べてみたら、こんなのが出てきました。
>正六面体群(物理のかぎしっぽ)
どうやら代数学のなかに群論というものがあって、
群論のなかで図形の回転対称を「回転群」で扱うようです。よくわかりません…。


コメント