問題ＰＤＦ
（１）
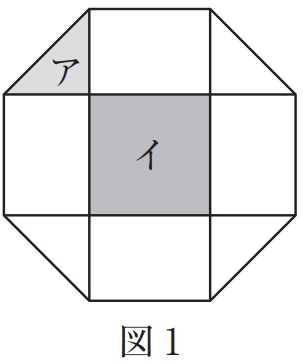
図１は正八角形を４本の線で分けたものです。
アの部分とイの部分の面積の比を最も簡単な整数の比で求めなさい。
（２）
図２のように正八角形と直線があります。正八角形の１辺が直線上にあるとき、その右側にある頂点を中心に、次の１辺が直線上にくるまで回転させることを「ころがす」ということにします。正八角形の１つの頂点Ｐを、直線上の点Ａからはじめて、１回ころがすごとに、頂点Ｐが移った先をＢ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ、Ｈとすると、図３のようになります。
もとの正八角形と八角形ＡＢＣＤＥＦＧＨの面積の比を最も簡単な整数の比で求めなさい。 
＠解説＠
（１）
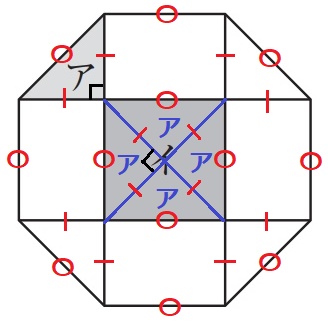
↑この分割は押さえておきたい。
アは正八角形の１辺〇を斜辺とする直角二等辺三角形。
イは〇を１辺とする正方形。これを４分割するとアと合同の直角二等辺になる。
ア：イ＝１：４
（２）
面食らう(;`ω´)
回転の中心から各点を結んでみる。（回転する角＝中心角は45度）
直線上の辺は、いずれも正八角形の１辺で長さが等しい。
正八角形の１辺と対角線をもとに●▲×を２個ずつあてはめると正八角形になる。
残りの二等辺三角形たちをどうすべきか…。
●と●は底辺と高さが一緒なので等積。●を正八角形の上側に移動する。
↑記号を打ちました。
ＢＪとＣＬは平行。Ｋを通る平行線をひき、ＢＣとの交点をＩとする。
ＪＫ：ＫＬ＝１：１から、ＩはＢＣの中点である。
△ＢＫＣを等積変形すると△ＩＪＬとなる。
ここで△ＩＪＬと△ＤＮＭに着目する。
Ｉは正八角形の高さの半分。
△ＩＪＬの底辺を半分、高さを２倍すると△ＤＮＭになる→△ＩＪＬと△ＤＮＭは等積（×）
正八角形を左のように３分割すると、
（ア×２＋★）：（ア×４＋★★）：（ア×２＋★）＝１：２：１
長方形の対角線で区切ると、正八角形が×で４等分される。
△ＩＪＬと△ＤＮＭは正八角形の４分の１（×）だから残りが埋まる。
ＭＮの右側も同様にすると、八角形ＡＢＣＤＥＦＧＨは正八角形３個分。
１：３
*良い解法を編み出した方は、下のコメント欄かお問い合わせよりお知らせ願いますm(_)m
難関中（算数科）解説ページに戻る
コメント