平均49.3点(前年比;-2.1点)
問題はこちら→リセマムさん
大問1(計算)
(1)
-7+5
=-2
(2)
(-3)×4-(-6)×4
=-12+24
=12
(3)
2/3÷(-8/3)+1/2
=-1/4+1/2
=1/4
(4)
4(-x+3y)-5(x+2y)
=-4x+12y-5x-10y
=-9x+2y
(5)
14√7+√3×√21
=2√7+3√7
=5√7
大問2(小問集合)
(1)
x2+5x-36
=(x+9)(x-4)
(2)
x=5を放り込んでaを求める。
3×5-4=5-2a
2a=-6
a=-3
(3)
因数分解ができないので解の公式。
x=〔-3±√{32-4・3・(-1)}〕/2・3
=(-3±√21)/6
(4)4<√n<10をみたす、nの個数を求める。
nに根号がついているので、2乗して外す。
42<√n2<102
16<n<100
16よりも大きく、100よりも小さい整数の個数が正解。
換言すれば、17~99の整数。
99-17+1=83個
(5)図形の点対称移動
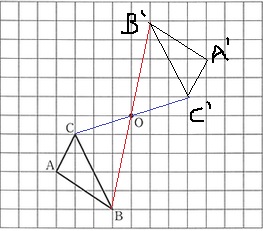
回転の中心Oと結び、距離が等しくなるようにB’とC’を作成。
AC//C’A’で、A→Cが右に1、上に2なので、C’→A’も同様。
大問3(小問集合2)
(1)角度
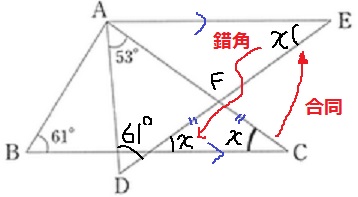
求める∠ACBをxとおく。xを合同で上にあげて、錯角で下ろす。
すると、二等辺三角形が登場する。
∠ADF=61°で、△ADFの外角定理から、
∠DFC(二等辺の頂角)=53+61=114°
x=(180-114)÷2=33°
(2)連立方程式
立式さえできれば正解◎
アは、じゃんけんの回数→10
イは、段差。〔兄-弟=-5〕となる→2x-3y
(3)確率
袋から取り出したものを戻して2回目をとる。
少なくとも1回は赤⇒全体-2回とも白(赤がでない)
白が出る確率は5分の2だから…
1-2/5×2/5=21/25
大問4(関数)
(1)
y=1/2x2から、A(4、8)
DはOBの中点なのでD(0、5)
D→Aで、右に4、上に3だから傾きは3/4
切片はD
AD:y=3/4x+5
(2)
△OABの面積は、10×4÷2=20
四角形ABCE=△OEC=10

△OECの底辺が6なので高さは、
10×2÷6=10/3…Eのx座標
OAの式はy=2xなので、
E(10/3、20/3)
大問5(平面図形)
(1)相似の証明

円周角定理と対頂角で2角が等しい→∽
これを前提に解く相似の問題はたくさんあるので、
ぜひ取っておきたい。
(2)
実際に作図してみよう。
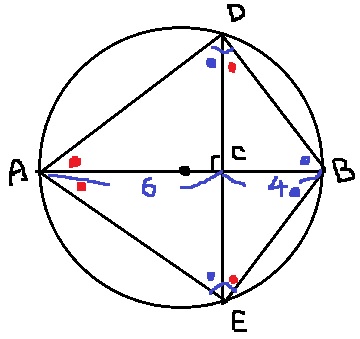
パッと見、△ABDと△ABEが合同に見える。
円周角や●+●=90°をもとに調べていくと、
一辺両端角相等でやはり合同。
上の三角形と下の三角形は直径ABをはさんで線対称。
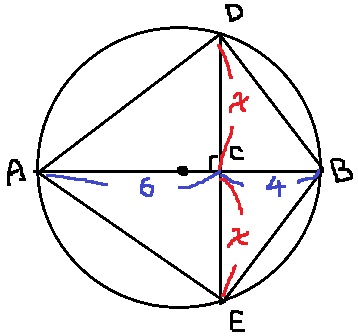
CD=CE。これをxとおく。
方べきの定理から、AC×CB=DC×CE
6×4=x2
x=2√6
(方べきの定理を知らない人は、前問の△ACD∽△ECBを利用して、
6:x=x:4の比例式から、外項と内項の積で式を立てればいい)
△ACDで三平方。
AD2=62+(2√6)2=60
AD=2√15cm
大問6(数量変化)
(1)
6分後~14分後(満水)を考える。
水面は40-20=20cm上がる…ア
8分間で水槽に入れた水の体積は40×40×20cm3
これを8で割れば、1分あたりの水の量がでる。
40×40×20÷8=4000cm3
(2)
グラフを使えば楽に求めることができる。
図1も図2も2つのおもりの配置を変えただけなので、
入れる水の量は同じだから、ともに14分後に満水になる。
おもりの影響をうけないところは水面の上昇率が等しい。
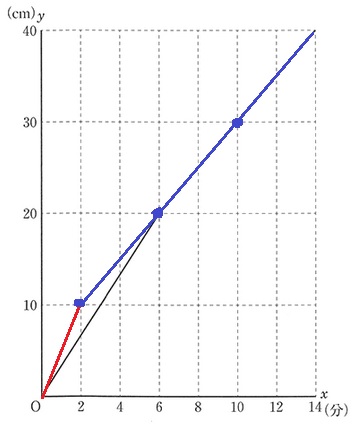
最後の線はかぶる。
おもりの高さは10cmなので、格子点を意識して青線をひく。
赤線に注目。
〔2分で10cm上昇〕
水深8cmは…2×8/10=8/5分後
大問7(データの活用)
(1)平均値と最頻値
0×0+1×1+2×1+3×1+4×3+5×0+6×2+7×2+8×0+9×1+10×0
=53
53÷11=4.81…→平均4.8回
最頻値は標本数が最も多い4回
(2)中央値
表2で残りの人数は6人⇒x+y=6
0≦x≦6…①
『2年生15人の中央値が6回』
(15+1)÷2=8番目が6回
表1と照らしながら、表2から2年生だけを抜き出す。
(以下、ボールの入った回数は〇で表しています)
【③×1、④×1、➄×x、⑥×4、⑦×1、⑧×y、⑨×2】
ここから、8番目が⑥になるように調整する。
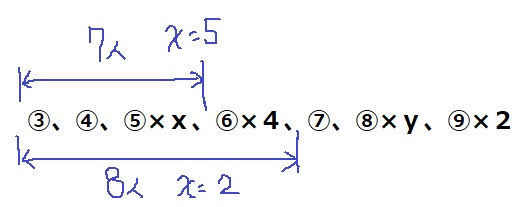
⑥の手前に7人いれば、8番目は⑥になる。
x=7-2=5人
⑥の4人目が8番目であればセーフ。
x=8-6=2人
2≦x≦5…②
①と②の共通する2≦x≦5→2、3、4、5
大問8(空間図形)
(1)
展開図に引きなおし、△AEGで三平方。
AG2=42+82=80
AG=√80=4√5cm
(2)切断面の作図は丁寧に!

AC//QRになる。正方形の対角線ですね。
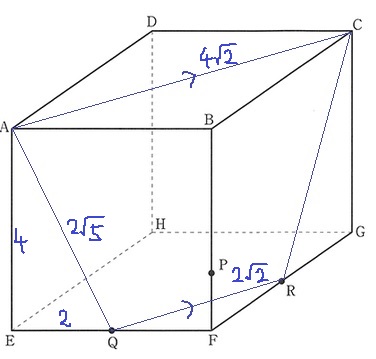
三平方を駆使する。高ささえわかればいい。
四角形AQRCが等脚台形。
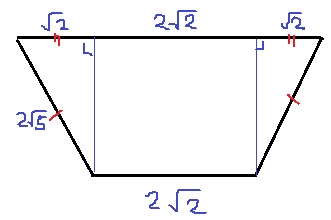
垂線を2本引くと、左右に合同な三角形ができる。
三平方で高さは、√{(2√5)2-(√2)2}=√18=3√2
(2√2+4√2)×3√2÷2=18cm2
@余談@
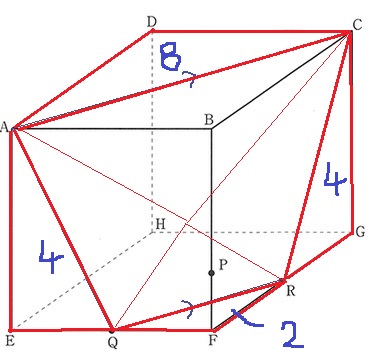
8+4+4+2=18cm2
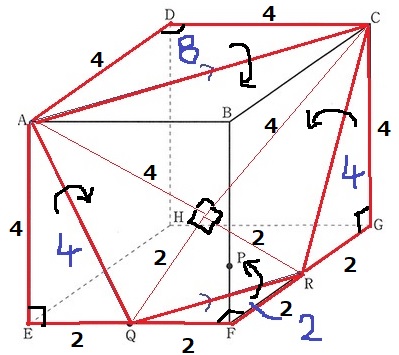
折り返すと等辺が重なり、さらに4つの90°が集まることで面がデコボコではない
→1つの面におさまる、ということになります。



コメント
なんで余談のところの解き方で解けるのですか?
コメントありがとうございます。
本文で少し追記しました。
あまり現実的ではない解法なので参考程度にしてください。