平均22.7点(50点満点;前年比-1.5点)
問題はこちら→リセマムさん
大問1(計算)
(1)
3/4×5/9
=5/12
(2)
7-2×(-3)
=7+6
=13
(3)
7x+y-(5x-8y)
=7x+y-5x+8y
=2x+9y
(4)
48a2b2÷(-4a)÷(-2b)2
=48a2b2÷(-4a)÷4b2
=-3a
(5)
(3x-1)2+6x(1-x)
=9x2-6x+1+6x-6x2
=3x2+1
(6)
√90+60/√10
=3√10+6√10
=9√10
大問2(小問集合)
(1)
(2x+9)/5=x ←両辺を5倍して左右入れ替え
5x=2x+9
x=3
(2)①
(2019-9)×2/3=1340
②
(y-9)×2/3=2
y=12
(x-9)×2/3=12
x=27
(3)ア
解の公式の結果を書く。
{(-b±√(b2-4ac)}/2a
イ
解の公式の証明。
教科書に必ず載っているが解けたかな?
方針としては、平方完成して左辺を2乗の形にする。
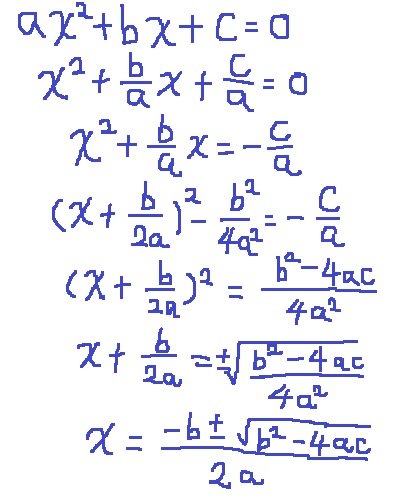
x2の係数2で割り、( )2=〇の形にもっていく。
2を外すと、右辺は±√〇となる。
√(4a)2=2a→+b/2aを右辺に移項して完了。
2b’=bの解の公式も、bを2b’に置き換えて同様の手法を用いる。
(4)
円の中心Pの作図。
①Aで直線ℓに接する。
⇒接線と半径は接点で垂直に交わる→Aを通る垂線の作図。
②AとBが円周にくる。
→AとBの垂直二等分線の作図。
2本の直線の交点がP
(5)①
(5・6・7)(+・-)(3・4)
1は素数ではない。
【2】…5-3、6-4
【3】…6-3、7-4
【11】…7+4
計5通り
カードの取り出し方は、3×2×2=12通り
5/12
②
和と差で奇数になる場合を考える。
偶+奇=奇、奇+偶=奇、偶-奇=奇、奇-偶=奇。
偶数と奇数をそれぞれ1つずつ出せばいい。
登場する数字は【3・4・5・6・7】
偶数が4と6しかない。
もし、箱Cに4を入れると(A、C)=(6、4)と偶数2連続の場合がでてくるので、
その分、偶数と奇数の双方がでてくる場合が少なくなってしまう。
4と6はバラけさせて、箱Aには4のカードを入れる。
ア…4
4+3、4+5、4-3、6+3、6+5、6-3、6-7
計7通り
7/12
(6)①
情報整理。
排水は毎分2Lで常時行われる。
給水は毎分5Lで、水槽が残り150Lになったら20分間行われる。
給水中は、5-2=毎分3L増える。
25分後に水槽は150L
水槽…150+3×(30-25)=165L
25分後にタンクは300L
タンク…300-5×(30-25)=275L
②
3回目に等しくなるとき⇒グラフで3回目に交わるところ。

75分のときに水槽とタンクの差は50L
毎分8Lで近づくので、50÷8=6・1/4=6分15秒
75分+6分15秒=81分15秒
大問3(データの活用)
(1)
最頻値(モード)は最もあらわれている値。
その階級は17~32
階級値は真ん中の値→(17+22)÷2=19m
(2)
25m以上投げた人は、7+3=10人
10/40=0.25
*相対度数は分数ではなく、小数で答える。
(3)
40人の中央値(メジアン)は、20番目と21番目の平均。
すなわち、aとbの平均。
aとbも17~21の階級にある。
中央値が18なので、この範囲にあり、平均が18となる2つの数の組合せが答えとなる。
(a、b)=(17、19)(18、18)
(4)
総和は【階級値×度数】
(7×3+11×4+15×6+19×11+23×6+27×7+31×3)÷40
=784÷40=19.6m
大問4(空間図形)
(1)①
AP:PO=2:4=1:2
△OABに注目。
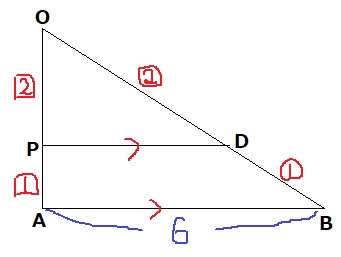
OP:PA=OD:DB=2:1
平方線と線分の比から、PD//ABとなる。
△OPD∽△OABより、
PD=6×2/3=4cm
②
PEについてもPDと同様なことがいえる。PE=4cm
OP=4cm
4×4×1/2×4×1/3=32/3cm3
(2)①
三角錐O-ABCの体積を【1】とすると、
三角錐O-PDEの体積は【1/3】となる。
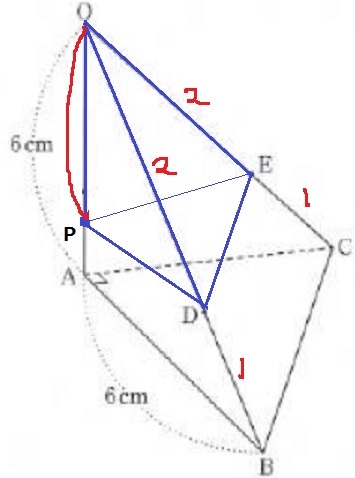
O-ABCの体積から、OA・OB・OC上の辺の比をかけるとO-PDEになる。
OP/OAを□とおくと、
【1】×2/3×2/3×□=【1/3】
□=3/4
OP=6×3/4=9/2
AP=6-9/2=3/2cm
②
Pから△ODE方向に垂線をひく。
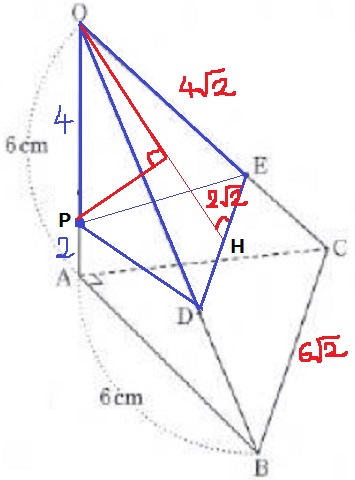
この垂線は、△ODEを底面としたとき、三角錐P-ODEの高さにあたる。
そこで、P-ODEの体積から垂線の長さを求める。
P-ODEはO-ABCの体積の3分の1なので、
6×6×1/2×6×1/3×1/3=12cm3
正三角形OBCの各辺は1:1:√2から6√2
OD:DB=OE:EC=2:1から、
正三角形△ODEの各辺は4√2cmとなる。
OからDE方向に垂線をひき、交点をHとする。
OH=√(4√22-2√22)=2√6cm
△ODEの面積…4√2×2√6÷2=8√3cm3
求める垂線の長さを□とおくと、
8√3×□×1/3=12cm3
□=3√3/2cm
大問5(関数)
(1)
y=-1/3x2にy=-3を代入してA座標を求める。
-3=-1/3x2
x<0より、x=-3
A(-3、-3)
直線ABは(-3、-3)と原点Oを通る。
ということは、AB:y=x
B(4、4)
これをy=ax2に代入する。
4=42a
a=1/4
(2)
y=1/4x2にx=-2を代入。
y=1/4×(-2)2=1
C(-2、1)
C(-2、1)⇒B(4、4)
右に6、上に3だから、傾きは1/2
4=1/2×4+b
b=2
y=1/2x+2
(3)①
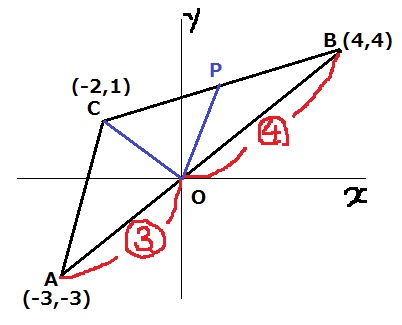
ABCの座標を確認。
AO:OBはx座標の比から3:4となる。
ここから、△CAO:△COB=3:4
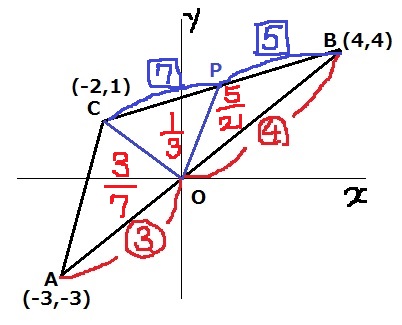
△ABCの面積を【1】とおく。
△CAO=【1】×3/7=【3/7】
△OPCの面積は【1/3】とするので、
△OBP=【1】-【3/7】-【1/3】=【5/21】
△OPC:△OBP=【1/3】:【5/21】=7:5
この2つの三角形は高さが等しいので、底辺CP:PB=7:5
Pのx座標…-2+6×7/12=3/2
(2)の式に代入。
Pのy座標…y=1/2×3/2+2=11/4
P(3/2、11/4)
②
Qのx座標は3/2
y=-1/3x2に代入。
Q(3/2、-3/4)
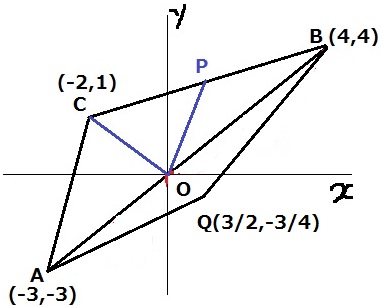
△ABC:△OPC=3:1なので、
△ABC:△ABQの面積比が出せれば、四角形AQBC(全体):△OPCがでる。
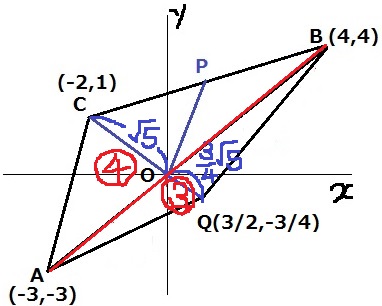
△ABCと△ABQは底辺ABを共通とする。
高さの比はCO:QO
CとQの座標を三平方の定理に放り込む。
CO=√{(-2)2+12}=√5
CQ=√{3/22+(-3/4)2}=3√5/4
△ABC:△ABQ=√5:3√5/4=4:3
△OPC=4×1/3=4/3
四角形AQBC:△OPC=7:4/3=21:4
四角形AQBCは△OPCの21/4倍
大問6(平面図形)
(1)
△ADC∽△BGFの証明。
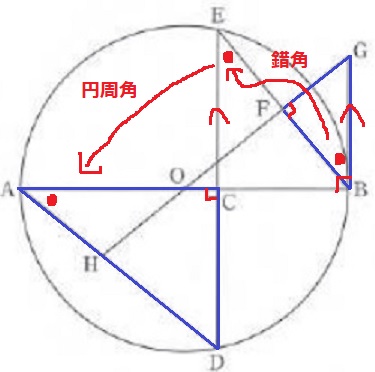
BGはBを接点とする円の接線。接線と半径は垂直に交わる。
ここから、DE//BGとなり、錯角→弧BDの円周角+直角で2角が等しい。
(2)①
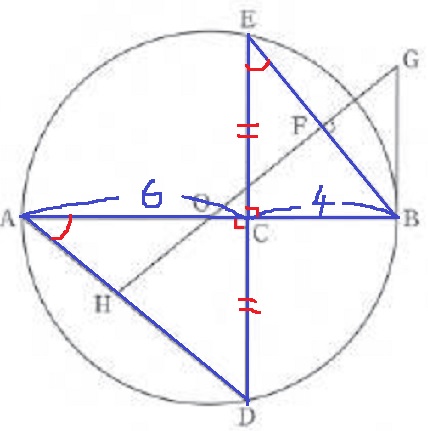
△ACD∽△ECB(2角相等)
直径ABを対称の軸とすると、上下のD・Eが対称関係となる。
DC=ECで、各々の長さをxとおくと、
6:x=x:4
x2=24
x>0から、x=2√6cm
*方べきの定理:AC×CB=DC×CE
@別解@
OEに補助線。半径でOE=5
OC=1
△EOCで三平方→CE=2√6cm
②
孤AEに対する円周角から、∠ADE=∠ABE
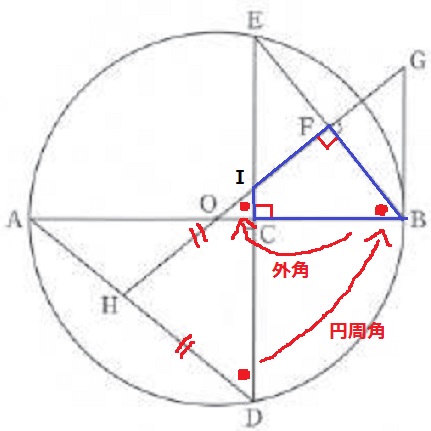
HGとEDの交点をIとし、四角形ICBFに注目。
∠ICB+IFB=90+90=180°
対角の和が180度である四角形は円に内接する。
円に内接する四角形の内角は、その対角の外角に等しい。
∠CBF=∠HID
△HDIは2つの底角が等しいので二等辺三角形。
HD=HI
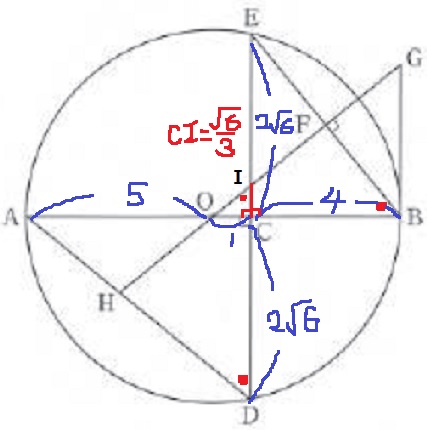
辺の長さを調査。
△ECB∽△OCI(2角相等)
CI=1×4/2√6=√6/3

HからIDに向けて垂線をひき、交点をJとおく。
ID=√6/3+2√6=7√6/3
二等辺三角形の頂角を通る底辺と垂直な線は、底辺を2等分する。
JD=7√6/3÷2=7√6/6
CJ=2√6-7√6/6=5√6/6
CJ:JD=5√6/6:7√6/6=5:7
AC//HJで、△ADC∽△HDJより、
AH:HD=5:7
△ADCで三平方→AD=2√15
DH=2√15×7/12=7√15/6cm
@別解@
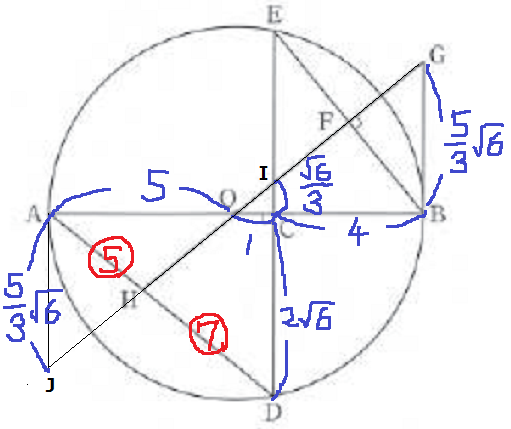
(1)で△ADC∽△BGFだったので、∠ADC=∠BGF
ここから、△ACD∽△OBG
BG=2√6×5/6=5√6/3
△OBG∽△OCI
IC=5√6/3×1/5=√6/3
Aを接点とする円の接線をひき、GHとの交点をJとする。
△AJO∽△GBO
AJ=BG=5√6/3
△AJH∽△DIH
AH:HD=5√6/3:7√3/3=5:7
△ACDで三平方、AD=2√15
DH=2√15×7/12=7√15/6cm
@別解@
おやじさんから素晴らしい解法を頂きました。
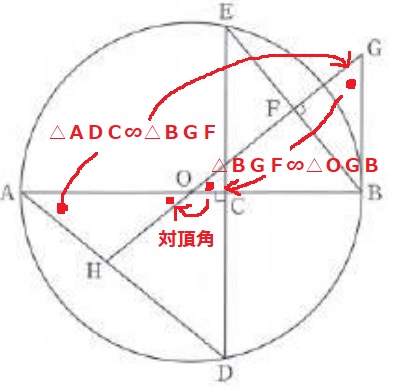
△ADC∽△BGF(前問の相似)→△BGF∽△OGB→対頂角の流れで、
2つの底角が等しくなり、△HOAが二等辺三角形となる。

HからAOに向けて垂線を引き、交点をIとする。
△HOAは二等辺なので、AI=IO=5/2
△OIH∽△OBGに注目。
IH:BG=IO:BO=5/2:5=1:2
BGは先ほどのように△ACD∽△OBGから、BG=5√6/3
IH=5√6/3×1/2=5√6/6
ここから、△AIH∽△ACDに視点を変える。
AH:AD=IH:CD=5√6/6:2√6=5:12
あとはADを求め、5/12倍で求められます。
*DHの長さを求めるので、Hの位置を確認しておく必要があります。
△HOAが二等辺であることを導いたうえで、Hからの補助線をAO方向にひき、
IHを1辺とする三角形と相似関係にある三角形を探します。
こちらの方が計算処理がスッキリしますね!



コメント