2019年度　栃木県公立高校過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）　98.2％
－７＋５＝－２

（２）　84.3％
（３ｘ－２）/５×１０
＝２（３ｘ－２）
＝６ｘ－４

（３）　86.4％
５ａｂ²÷ａ/３
＝５aｂ²×３/ａ＝１５ｂ²

（４）　89.9％
（ｘ＋８）（ｘ－６）
＝ｘ²＋２ｘ－４８

（５）　59.7％
２５の平方根を求める。
□×□＝２５
□＝±５

（６）　75.8％
多角形の外角の和は３６０°
ｘ＝３６０－（６０＋９０＋３５＋１０５）
＝７０°

（７）　80.7％
反比例の式に代入。
－２＝ａ/６
ａ＝－１２　反比例の比例定数ａ＝ｘｙ

（８）　55.2％
面積比は辺の比の２乗。
△ＡＢＣ：△ＤＥＦ＝４：９
よって、８×９/４＝１８ｃｍ²

（９）　81.2％
連立方程式。加減法が多いかな？
ｘ＝－３、ｙ＝４

（10）　85.6％
大きいサイコロで〔何か〕を出す。
小さいサイコロで、その〔何か〕が出るのは１/６

（11）　80.3％
∠ＢＯＣ＝３６０－２４８＝１１２°
円周角定理から、∠ｘ＝１１２÷２＝５６°

（12）　70.4％
解の公式
ｘ＝{－７±√（７²－４・1・1）}/２・１
＝（－７±√４５）/２＝（－７±３√５）/２

（13）　52.8％
ｙ＝150－２ｘ
ｙ＝－２ｘ＋150　⇒一次関数ウ

（14）　64.9％
ピラミッドの形ですね。四角錘ア

大問２（小問集合２）

（１）　56.0％
作図。
斜辺をＡＣとする直角三角形⇒∠ＡＢＣが９０°
①Ｂを通る半直線ＡＢと垂直な線をひく。
②それとℓとの交点が点Ｃ

（２）　73.9％
整数の性質に関する証明。
千の位…ａ、百の位…ｂ、十の位…ｂ、一の位…ａ
→①…ｂ、②…ａ

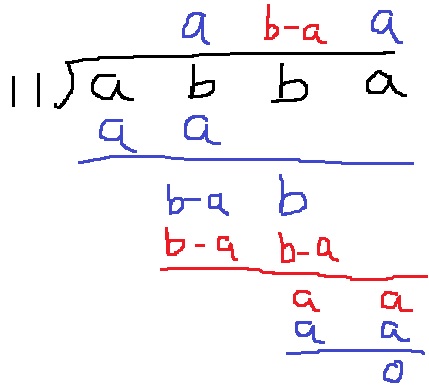
Ｎ＝1000ａ＋100ｂ＋10ｂ＋ａ
＝1001ａ＋110ｂ
＝１１（９１ａ＋１０ｂ）
→③…１１、④…９１、⑤…１０

１１の倍数であることを証明したいので、最後は１１でくくる形にもってくる。

＠余談＠

強引に筆算で割ってみたらできた。

＠11の倍数＠
覚える必要性は乏しいですが、11の倍数にはルールがあります。
〔各位を交互に足し引きして１１で割れたら１１の倍数〕
505582だったら、
５－０＋５－５＋８－２＝１１　→505582は１１の倍数
奇数の位（一、百、万…）の和と偶数の位（十、千、十万…）の和を合算して、
11の倍数だったら11の倍数。

11で割ったときの余りに注目する。
奇数の位で、１＝11×０+1、100＝11×9+1、10000＝1111×9+1
偶数の位で、10＝11×1-1、1000＝11×91-1、100000＝11×9091-1
＋１と－１で相殺すれば、余りがなくなって１１の倍数になる。
〔ａｂｂａ〕だったら、（ａ＋ｂ）－（ｂ＋ａ）＝０
０も１１の倍数（11×０）だから、ａｂｂａは１１の倍数。
専修大学松戸中学で11の倍数の判定法を丁寧な誘導をたどって仕組みを解明する問題が出ました。

（３）　28.3％！
ｙ＝ａｘ²から、
Ａのｙ座標は３６ａ、Ｂのｙ座標は１６ａ
Ａ→Ｂの変化の割合が、ＡＢの傾き－１/２と等しいことを利用する。
（１６ａ－３６ａ）/{４－（－６）}
＝－２０ａ/１０
＝－２ａ＝－１/２
ａ＝１/４

大問３（文章題）

（１）　34.2％（部分正答含む54.6％）
一次方程式の記述問題。
文章題では正確な情報整理を！
Ａ店ではｘ本を、Ｂ店では（50－ｘ）本を買う。
Ａ店では２割引き→定価の８割で買う。
Ｂ店では定価で買ったが、割引券の使用で－500円。
150×８/10×ｘ＋{150×（50－ｘ）－500}＝6280
ｘ＝２４

（２）①　43.8％
ア：度数が最も大きい階級→20-24。×
イ：12-16の階級の１人は最小値の12個。14個食べた人は０人。×
ウ：24～40において、最も小さい度数は32-36の２人。×
エ：範囲（レンジ：range）＝最大値－最小値＝３９－１２＝２７個。○

②　15.4％！（部分正答含む46.4％）
いちごを26個以上食べた人数が、参加者の半数以下であることを説明する。
２６が中央値よりも大きいことを指摘する。

大問４（図形）

（１）　21.7％！（部分正答含む76.2％）
相似の証明。
∠ＡＢＣと∠ＥＢＤが共通角。
わざわざ辺の長さが与えられているということは、
２辺の比と間の角を使うと想像する。
ＡＢ：ＥＢ＝10：５＝２：１
ＢＣ：ＢＤ＝８：４＝２：１　→∽
対応する順番にアルファベットを書けるようにしよう。

（２）①　51.8％
円柱の高さは円の直径→８ｃｍ
４×４×π×８＝１２８πｃｍ³

②　2.9％!!
円がでてきたら、とりあえず半径の作図。

↑これが見えたらしめたもの。
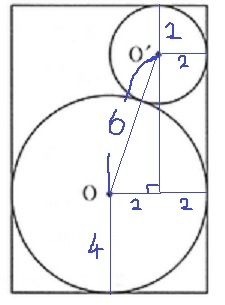
直角三角形の高さは、
√（６²－２²）＝４√２
円柱の高さは、２＋４√２＋４
＝６＋４√２ｃｍ

大問５（数量変化）

（１）　83.2％
グラフの読み取り。
忘れ物を気付いたのは、家をでてから８分後。
家から６００ｍの地点。

（２）　36.5％（部分正答含む46.3％）
記述式。

↑ここを求めよということ。
傾きと切片を頑張って求める。
ｙ＝６０ｘ＋１２０

（３）①　52.6％
公式解答参照。
家；７時６分から学校；７時25分を直線で結ぶ。

②　18.6％！
これも同様に直線でひいてみる。

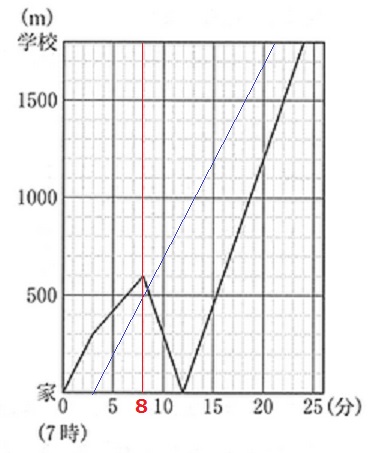
８分後に両者は１００ｍ離れている。
あすかは分速150ｍ、太郎は分速100ｍだから、
１分間で250ｍずつ近づいていく。
100÷250＝２/５分…８分後から２人が出会う時間
２/５分間で太郎は、100×２/５＝４０ｍ移動するので、
２人がすれ違う場所は家から５００＋４０＝５４０ｍ

＠別解＠

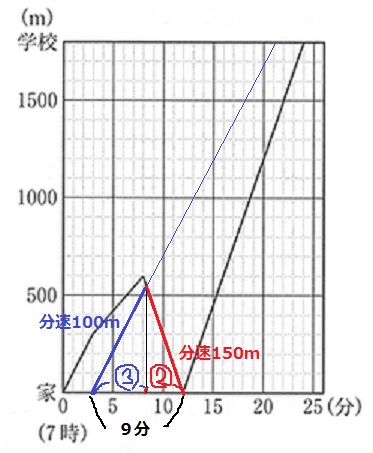
これも中学入試の解き方だが、、下の三角形に注目する。
高さは距離。
この距離を２：３の速さで走るので、
時間は逆比で３：２
太郎が出発してから、９×３/５＝２７/５分後に出会う。
１００×２７/５＝５４０ｍ

大問６（規則）

（１）　69.8％
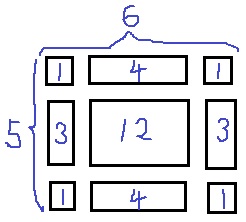
図３を観察しよう。
四隅が②。四隅以外の周りが③。中が④
３種類に分かれる。

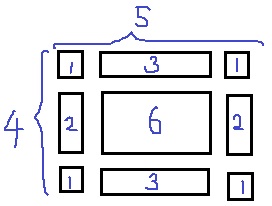
円の個数を調べる。
③のところは（１辺－２）個。
④のところは縦と横の積になる（↑であれば２×３＝６個）。
③の円盤の枚数は１０枚。

（２）　43.9％
前問と同様。

②×４＋③×１４＋④×１２
＝９８

（３）　4.9％!!（部分正答含む16.7％）
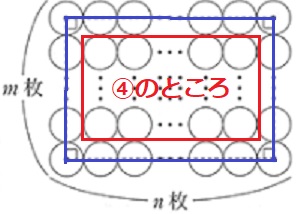
今までの規則を文字を使って一般化する説明記述。
四隅は…②×４
四隅以外の周り…③×（ｘ－２）×４
中…④×（ｘ－２）²
２×４＋３×４（ｘ－２）＋４×（ｘ－２）²＝４４０
問題文より、ｍ,ｎ≧３とあるので、ｘ≧３だから、
ｘ＝１１

（４）　0.2%!!!（部分正答含む1.0％）

青の長方形の面積が７８０ｃｍ²になる。
④が書かれた円盤の枚数を最も多くするには、
青がどのような長方形になればよいだろう？

正方形です。
④の円を最も多くするには、
中に円をギュッと集める必要がある。
縦長や横長の長方形にしてしまうと、
③の数が多くなり、その分、④の個数が減ってしまう。
だから、正方形に近い長方形にする。
（栃木数学の最後はいつも正方形問題がでてくるので、過去問を解いた受験生は気づけたはず）

７８０を素因数分解すると、２×２×３×５×１３
〔〇×△〕で〇と△の数をできるだけ近づかせる。
〔２６×３０〕が最も正方形に近くなる。
数的センスも問われる。コツは最小の２と最大の１３をかけ合わせ、
〔２、３、５、２６〕と数を減らしていき、〔２６、３０〕に持っていく。

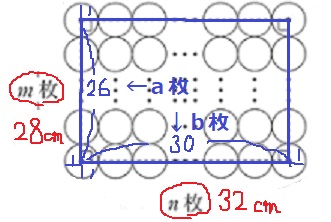
ｍ＝ａ＋１、ｎ＝ｂ＋１としているのは、両端に半径１ｃｍがあり、
縦ｍ枚から円１枚をとりのぞいた長さがａ枚の長さで、
横ｎ枚から円１枚をとりのぞいた長さがｂ枚の長さになるから。
つまり、長方形の縦２６ｃｍがａ枚分、横３０ｃｍがｂ枚分。
円の直径は２ｃｍなので、
ａ＝２６÷２＝１３枚、ｂ＝３０÷２＝１５枚

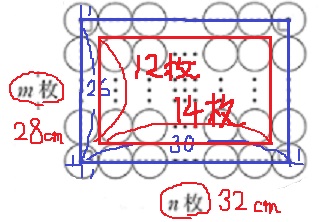
ごちゃごちゃして申し訳ない(;^ω^)
④は赤い線の範囲。
青の長方形から縦横１ｃｍ減るので、円１枚分が減る。
１２×１４＝１６８枚
公立高校入試解説ページに戻る