2019年度　三重県公立高校過去問前期【数学】解説

問題はコチラ→ＰＤＦファイル
後期解説はコチラ。

大問１（計算）

（１）
－18÷３²
＝－18÷９＝－２

（２）
４（ｘ－１）＋３（ｘ－２）
＝４ｘ－４＋３ｘ－６
＝７ｘ－10

（３）
６ｘｙ÷（－２ｘ）²×（－12ｘ²ｙ）
＝６ｘｙ÷４ｘ²×（－12ｘ²ｙ）
＝－18ｘｙ²　←ここで代入
＝－18×（－２）×（１/３）²
＝４

（４）
ｘ＋ｙ＝５、ｘ＋２ｙ＝４
連立を組んで解くと、ｘ＝６、ｙ＝－１
－１＝６ａ＋１
ａ＝－１/３

（５）
（√５＋２）（√５－７）－５/√５
＝５－５√５－14－√５
＝－９－６√５

（６）
（ｘ－５）（ｘ＋２）＝－10
ｘ²－３ｘ＝ｘ（ｘ－３）＝０
ｘ＝０、３

（７）
ａが正、ｂが負で、ａ＋ｂが負ということは、
絶対値でいえば、│ａ│＜│ｂ│
ａ＝２、ｂ＝－50と適当な値を入れて計算するのも良い。
ｂ－ａ＜ｂ＜－ａ＜ａ＜－ｂ＜ａ－ｂ

（８）
Ａ組の生徒数をｘ人とおく。Ｂ組の生徒数は70－ｘ人。
81ｘ＋88（70－ｘ）＝84.4×70
81ｘ＋6160－88ｘ＝5908
ｘ＝36　→36人

（９）
135°の作成。
135＝90＋45
①ＡＯを延長して180°を作成。
②Ｏを通るＡＯに垂直な線分を作成。
③Ａと反対側の90°を二等分する。
二等分線と孤ＡＢとの交点がＣとなる。

大問２（データの活用・確率）

（１）①
４/25＝0.16
*相対度数は分数ではなく、小数であらわす。

②
ア＋イ＝25－（３＋５＋４＋１）＝12
最頻値はイの階級にあるので、アは５以下でなければならない。
（６だとア・イが同数となるので）

25人の中央値は、（25＋１）÷２＝13番目の値。
もし、アが４だと13番目が22～26の階級になってしまう→４以下ではダメ。
よって、アは５となる。
イ：12－５＝７
ア…５、イ…７（完全解答）

（２）①
６つから３つを選ぶ→₆Ｃ₃＝20通り

↑正三角形は赤と青の２通りしかない。
２/20＝１/10

②
二等辺三角形を探す。

わかりにくくて申し訳ない（＾＾;
正六角形の隣同士の２辺で二等辺を作る。
頂角がＡ・Ｂ・Ｃ・Ｄ・Ｅ・Ｆと６つなので、合計６つ。
前問の正三角形を合わせて８つ。
８/20＝２/５

大問３（数量変化）

（１）
Ｐは３ｃｍ、Ｑも３ｃｍ移動。
３×３×１/２＝９/２ｃｍ²

（２）
４≦ｘ≦８のとき、ＰはＡＢ上、ＱはＣＤ上を動く。

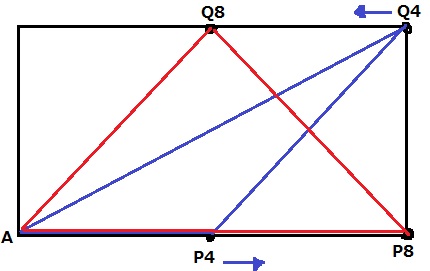
青→赤に変わる。
高さが変わらない。底辺だけ長くなる。
ＡＰ＝ｘｃｍなので、
ｙ＝ｘ×４÷２＝２ｘ
ｙ＝２ｘ

（３）
０≦ｘ≦４のとき、底辺ＡＰと高さＱＢがともに増加するので、
△ＡＰＱの面積は倍々に増えていく→放物線

４≦ｘ≦８のとき、前問から底辺だけ増加するので直線で上がる。
８≦ｘ≦12のとき、底辺が短くなるので面積は減っていく。
減り具合は４≦ｘ≦８のときに増加した変化の割合と同じ。
イ

（４）
長方形の面積の６分の１になので、
△ＡＰＱの面積：８×４÷６＝16/３ｃｍ²
ｙ＝16/３のときのｘの値が答えとなる。

ここで先ほどのイのグラフを拝借。
16/３は５ちょいなので、横線をひくと交点が１つしかない。
この点のｘ座標を求める。

０≦ｘ≦４の放物線ｙ＝ａｘ²は（４、８）を通るから、
８＝16ａ
ａ＝１/２
ｙ＝１/２ｘ²

１/２ｘ²＝16/３
ｘ²＝32/３
ｘ＝√32/√３＝４√６/３

（５）
区切りの良いところで分けて調べてみる。

０～４は直角ができなさそう。

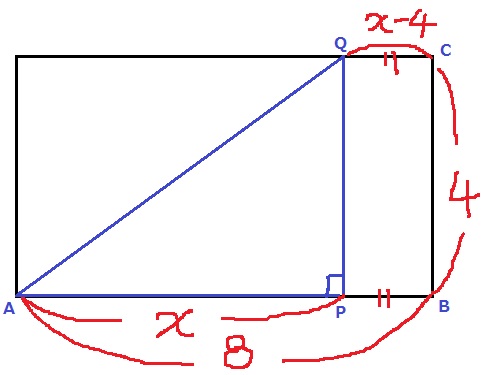
ＰがＱの真下にくると１つ目の直角。
Ｑが進んだ距離はＰと同じｘｃｍ。
ＱＣ＝ＰＢ＝ｘ－４ｃｍ
ｘ＋（ｘ－４）＝８
ｘ＝６

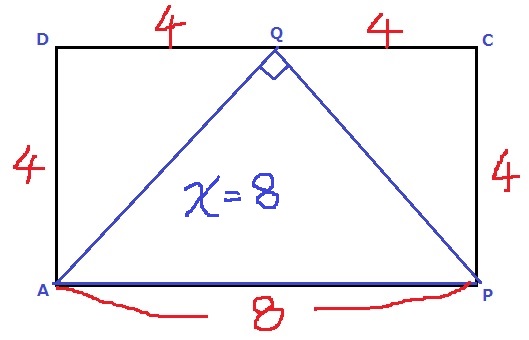
（２）でも出てきた。ｘ＝８のときは直角二等辺三角形になる。

最後も直角二等辺になる。
よって、ｘ＝６、８、12

大問４（空間図形・整数）

（１）
『底面の直径が高さと等しい円柱』なので、
円柱の底面の半径は６÷２＝３ｃｍ
（図２の球を円柱にスポッといれると内接する）
円柱の体積…３×３×π×６＝54πｃｍ³

球の体積…４/３πｒ³
＝４/３π×３³＝36πｃｍ³
よって、54π－36π＝18πｃｍ³
*円柱の体積を２/３倍すると球になる。

（２）①
完全解答。
２＋２＋２＋２＝８
２＋２＋２－２＝４
２＋２－２－２＝０
２－２－２－２＝－４
－４、０、４、８

②
最大値…全部＋⇒ａがｎ個あるから、ａｎ。
最小値…全部－⇒ａ－ａ－ａ－ａ－ａ…
－ａはｎ－１個ある。
はじめのａから、－ａ（ｎ－１）とひく。
ａ－ａ（ｎ－１）＝－ａｎ＋２ａ
したがって、ａｎ－（－ａｎ＋２ａ）＝２ａｎ－２ａ

③
完全解答。
２ａｎ－２ａ＝50　←両辺を÷２
ａｎ－ａ＝25
ａ（ｎ－１）＝25

ａ×（ｎ－１）すると積が25になる。
ａとｎは自然数なので、
ａ、ｎ－１の組み合わせは、（１、25）（５、５）（25、１）のみ。
ａ＝１、５、25
（*ｎの値はそれぞれ26、６、２となる。
ａ＝25、ｎ＝２であれば、25＋25＝50、25－25＝０、50－０＝50）

大問５（平面図形）

（１）
△ＢＦＨ≡△ＧＦＥの証明。

対頂角は等しい。ＢＨ//ＣＧから錯角。

合同の証明なので、３辺のうちいずれかの辺の長さが等しい点を指摘しなければならない。
そこで、公式解答の例１はＦがＡＤの中点であることから、△ＡＦＨ≡△ＤＦＥを経由している。
この２つの三角形は一辺両端角が等しいので合同。
ここから対応する辺ＦＨ＝ＦＥが得られ、一辺両端角から△ＢＦＨ≡△ＧＦＥとなる。

例２は、平行四辺形ＡＢＣＤに着目をしている。
対辺でＦＤ//ＢＣ。
ＦがＡＤの中点にあるので、ＦＤがＢＣ（平行四辺形の横）の半分にあたる。
中点連結定理の逆からＦがＧＢの中点にあり、ＧＦ＝ＢＦが導ける。
*中点連結定理の逆…三角形の 2 辺の上に端点を持つ線分が、残りの 1 辺と平行かつ長さがその辺の半分となるとき、線分の端点は各辺の中点になる。

（２）①
先ほどの合同証明の例１で、△ＡＦＨ≡ＤＦＥに言及したが、
同じことが△ＤＧＦ≡△ＡＢＦにも言える。

↑一辺両端角より合同。
△ＡＢＦの面積を求めればいい。
平行四辺形ＡＢＣＤが６ｃｍ²で、対角線ＢＤで区切ると、
△ＡＢＤ＝３ｃｍ²
ＦはＡＤの中点だから、△ＡＦＢ＝３÷２=３/２ｃｍ²
△ＤＦＧ＝３/２ｃｍ²

②
△ＤＦＥと△ＢＣＩの面積が等しい。
底辺の比ＦＤ：ＢＣ＝１：２なので、高さの比を２：１にすればいい。

高さの比はＦＢ上で考える。
△ＢＣＩの高さの比を□１とおくと、△ＤＥＦの高さの比は□２。
ＥはＤＣの中点なので、Ｅを通るＢＣに平行線をひくと、
ＦＢ上で□２は上のようになる。

ＦはＢＧの中点（△ＧＦＤ∽△ＧＢＣ、または先ほどの中点連結定理の逆）だから、
ＢＩ：ＩＧ＝１：７

③
前問のクリアがほぼ前提。

ＢＣ＝４ｃｍ
平行四辺形ＡＢＣＤの高さは、６÷４＝３/２ｃｍ
前問の高さの比から、ＢＩ：ＩＦ＝１：４なので、
△ＢＣＩの高さは、３/２×１/４＝３/８ｃｍ

回転体の体積は、底面の半径が３/８ｃｍで高さ４ｃｍの円柱に等しい。
３/８×３/８×π×４×１/３＝３/16πｃｍ³
公立高校入試解説ページに戻る