平均52.6点（前年比；＋0.3点）
出題範囲の縮小は資料の活用（標本調査）。
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１） 97.9％
－７－（－２）
＝－７＋２＝－５
（２） 98.1％
－６ｘ2ｙ÷２ｘｙ
＝－３ｘ
（３） 98.1％
４√５－√20
＝４√５－２√５
＝２√５
（４） 86.7％
ｘ2－４ｙ2
＝（ｘ＋２ｙ）（ｘ－２ｙ）
（５） 88.8％
ｘ2－３ｘ－５＝０
解の公式を適用して、ｘ＝（３＋±√29）/２
（６） 65.2％
球の表面積Ｓ＝４πｒ2
４π×２2＝16πｃｍ2
（７） 80.2％
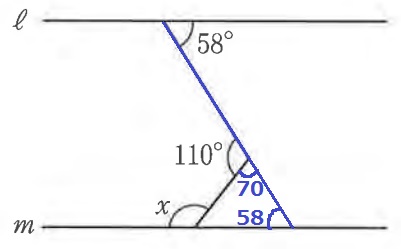
錯角で58°を下ろす。
180－110＝70°
最後に外角定理で、ｘ＝70＋58＝128°
（８） 65.9％
25人の中央値（メジアン）は、（25＋１）÷２＝13番目
表から13番目は400～500ｇの階級。
３/25＝12/100＝0.12
大問２（数量変化）
（１） 86.8％
ＢはＡと同時に出発して、Ａより５分早く着くから30分間走り続ける。
2700÷30＝分速90分
（２）ア88.8％、イ85.7％、ウ85.1％
自転車の時間をａ分、歩いた時間をｂ分とする。
時間の合計で等式⇒ａ＋ｂ＝35 …①
距離の合計で等式⇒160ａ＋60ｂ＝2700 …②
うえの連立を解く。②－①×60が良いかな？
ａ＝６、ｂ＝29
自転車の時間は６分で、歩いた時間は29分。
ア…160ａ＋60ｂ、イ…６、ウ…29
（３） 39.4％
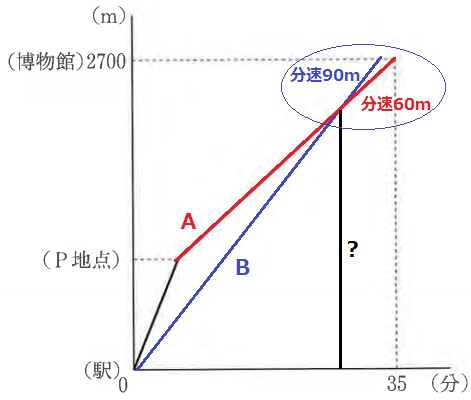
Ｂをグラフに載せる。
交差するポイントがＢがＡに追いついた地点。
ゴール付近をピックアップする。
Ｂが到着した５分後にＡが到着する。
Ｂ到着時に、Ａは60×５＝300ｍ後方にいた。
両者の差は１分あたり、90－60＝30ｍずつ拡大していく。
ＡとＢが同じ場所にいた地点から300ｍの差が開くのは、
300÷30＝10分後
？の距離は、90×10＝900ｍ
よって、駅からＢがＡに追いついた地点までの距離は、
2700－900＝1800ｍ
大問３（図形）
（１）ⅰ89.0％、ⅱ91.2％
△ＡＢＥ∽△ＢＤＥの証明。
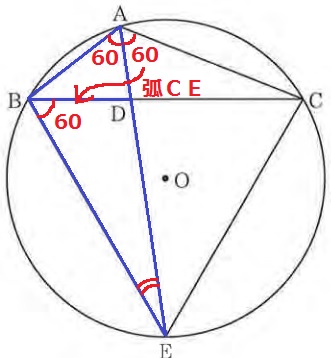
共通角で∠ＡＥＢ＝∠ＢＥＤ
仮定より、∠ＢＡＥ＝∠ＣＡＥ
弧ＣＥに対する円周角で、∠ＣＡＥ＝∠ＤＢＥ
∠ＢＡＥ＝∠ＤＢＥとなり、２角が等しく∽。
ⅰ…ウ、ⅱ…カ
（２） 42.3％
前問の相似を利用する。
対応する辺がごちゃごちゃになったら、三角形を描いてみよう。
ＤＥ＝７×７/８＝49/８ｃｍ
（３） 32.5％！
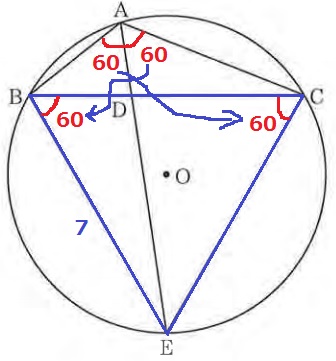
ポイントは60°。
円周角定理で60°を移動すると、△ＢＣＥの内角はすべて60°で正三角形。
１辺７ｃｍの正三角形の面積を求めればいい。
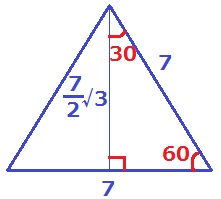
縦に割ると１：２：√３の直角三角形。
高さは７×√３/２＝７√３/２ｃｍ
７×７√３/２÷２＝49√３/４ｃｍ2
（４） 1.0％!!!
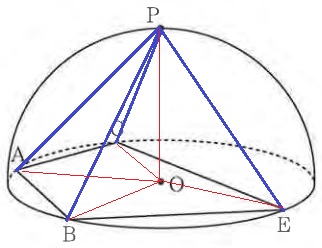
四角錘の体積＝底面の四角形ＡＢＥＣ×高さＰＯ÷３
高さＰＯは球Ｏの半径＝円Ｏの半径に相当する。
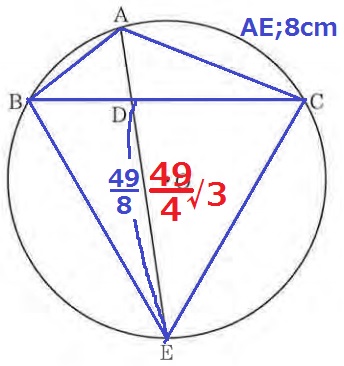
前問の解答をフル活用できる。
△ＡＢＣと△ＢＣＥは底辺がＢＣで共通するので、高さの比がＡＤ：ＤＥ。
ここから四角形ＡＢＥＣ：△ＢＣＥ＝ＡＥ：ＤＥ＝８：49/８＝64：49
四角形ＡＢＥＣの面積は、49√３/４×64/49＝16√３ｃｍ2
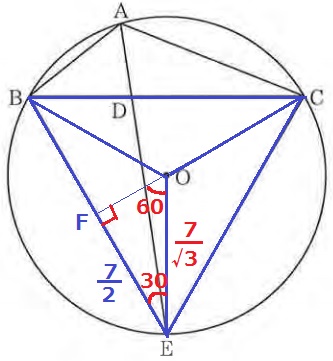
円の半径も正三角形ＢＣＥを使う。
うえのように分割すると合同な二等辺三角形が３つできる。
それを二等分した△ＯＦＥは１：２：√３の直角三角形。
ＦＥ＝７÷２＝７/２ｃｍ
半径ＯＥ＝７/２×２/√３＝７/√３ｃｍ
四角錘Ｐ―ＡＢＥＣの体積は、16√３×７/√３÷３＝112/３ｃｍ3
大問４（関数）
（１） 81.7％
ｙ＝８/ｘにｘ＝４を代入。Ａ（４、２）
ＡＢの中点が原点Ｏということは、Ｂは原点ＯについてＡと対称。
Ｂ（－４、－２）
（２） 83.3％
Ａ（４、２）をｙ＝ａｘ2に代入。
２＝４2ａ
ａ＝１/８
（３）①ア54.8％、ｲｳ40.8％
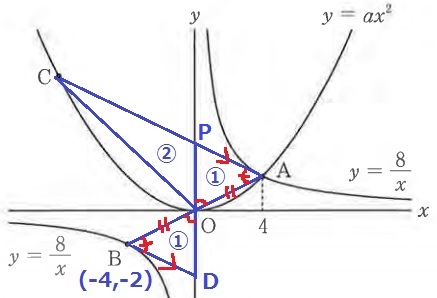
ＣＡとｙ軸との交点をＰとする。
△ＡＰＯと△ＢＤＯにおいて、仮定よりＡＯ＝ＢＯ
ＣＡ//ＢＤから錯角で∠ＰＡＯ＝∠ＤＢＯ、対頂角で∠ＰＯＡ＝∠ＤＯＢ
１辺と両端角が等しく、△ＡＰＯ≡△ＢＤＯ
△ＢＤＯの面積を①とすると、△ＡＰＯ＝①、△ＣＰＯ＝②
合同でＯＰ＝ＯＤだから、△ＣＰＯの高さは△ＢＤＯの高さの２倍。
Ｂのｘ座標が－４なので、Ｃのｘ座標は－８。
ｙ＝１/８ｘ2において、ー８≦ｘ≦４のとき、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－８のとき、最大値ｙ＝８
０≦ｙ≦８
ア…－８、イ…０、ウ…８
② 6.8％!!
△ＡＣＥの３辺の和を最小にする。
辺ＡＣの長さは固定なので、辺ＡＥ＋辺ＥＣの長さを最小にすればいい。
Ｃをｘ軸について対称移動させたＣ’（－８、－８）とＡ（４、２）を結ぶ。
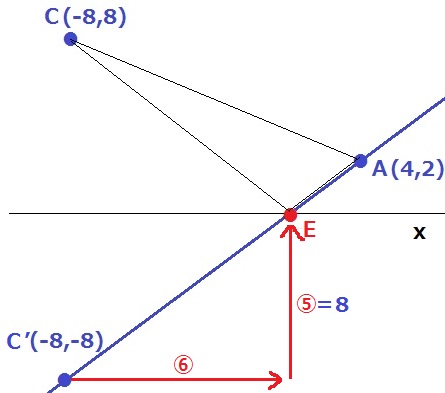
Ｃ’⇒Ａは右に12、上に10移動するので、傾きは10/12＝５/６
Ｃ’から右に⑥、上に⑤移動してＥ座標。
⑤が８だから、Ｅのｘ座標は－８＋８×⑥/⑤＝８/５
大問５（確率）
（１） 37.9％
６枚の中から表が出た２枚を選ぶ。
6Ｃ2＝15通り
（２） 37.6％
表０枚⇒１通り
表１枚⇒6Ｃ1＝６通り
表２枚⇒前問の15通り
表３枚⇒6Ｃ3＝20通り
表４枚⇒裏となる２枚を選ぶので表２枚と同じ15通り
表５枚⇒裏となる１枚を選ぶから６通り
表６枚⇒１通り
（１＋６＋15）×２＋20＝64通り
（３）① 11.8％！
ａが平方数になれば、ルートが外れて整数になる。
■表が１枚
１、４、９
■表が２枚
１×４、１×９、２×８、４×９
以上、７通り。
② 2.9％!!
すんごく大変です(-_-;)
あてずっぽうでは困難なので、まずは素因数分解。
１＝１
２＝２
４＝２×２
６＝２×３
８＝２×２×２
９＝３×３
平方数にするためには、素因数２か３を偶数個にする。
３の素因数は９が２つだが、６は１つしかないので奇数個になってしまう。
→６は絶対使えない。
■表が３枚
１×２×８、１×４×９（表２枚の２×８と４×９の組み合わせに×１を追加）
２×４×８、２×８×９
■表が４枚
１×２×４×８、１×２×８×９
２×４×８×９
■表が５枚
１×２×４×８×９
忘れてはならないのが、すべて裏の場合はａ＝０となり、√０＝０で整数である！
全部で、７＋４＋３＋１＋１＝16通り
確率は、16/64＝１/４
大問６（規則）
（１） 67.3％
実際に２つ目とばしで書いてみるとイしかない。
ア・ウは点が偶数個なので、正多角形になってしまう。
イ
（２）①16.9％！、②13.1％！
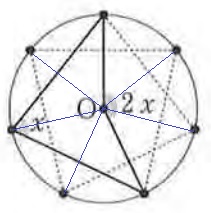
２ｘは360°を７等分したうちの３個分。
３：７＝２ｘ：360
内項と外項の積で、
７×２ｘ＝３×360 ←両辺を÷２
７ｘ＝540
①…３、②…540
（３） 4.8％!!
前問の７個の場合を考えてみよう。
円を７等分した場合、左が４個分で右側が３個分であった。
円をｎ等分した場合、４個分とｎ－４個分に分かれる。
先ほどの比例式のように計算すると、
【ｎ－４：ｎ＝２ｘ：360】
ｎ×２ｘ＝（ｎ－４）×360
ｎｘ＝180（ｎ－４）
先端部分のｎ個の角の和は、180（ｎ－４）°となる。
＠余談＠
ｍ点ごとに結んだ星形ｎ角形の先端部分の角の和は、180（ｎー２ｍ）°になる。
（４） 9.8％!!
星形多角形はどんなときに作られるか。
１つ目ごと、２つ目ごと…で整理すると以下のようになる。
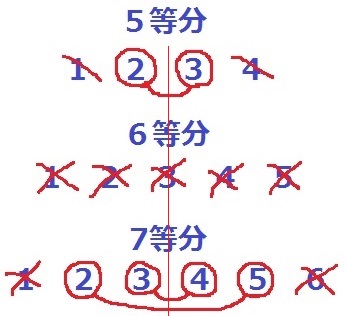
◆５等分
１つ目ずつ（隣同士を結ぶ）では正五角形になるので１は×。
４つ目ずつはスタートの点の隣になってしまうので、〇等分－１も×。
（１つ目ずつを反時計回りで結んだら、４つ目ずつは時計回りに１つ目ずつ結ぶのと同じ）
２つ目ずつと３つ目ずつはＯＫ。両者は同じ星形。
◆６等分
先の同じ理由で１と５は×。
２と３は６の約数なので１周するとすべての点を通過せず、正多角形になってしまう×。
４つ目ずつで試してみると、４→２（８）→６（12）で正三角形になってしまう。
４がダメなのは、６と同じ共通の約数（公約数）２を含んでいるからである。
公約数があるとすべての点を通過しない。（公約数２であれば偶数番目の点だけ）
◆７等分
１と６は×！
２・３・４・５と７は互いに素で公約数を持たない。どれでもＯＫ！
また、真ん中を縦線で仕切ると、線対称で同種の星形がペアにあらわれる。
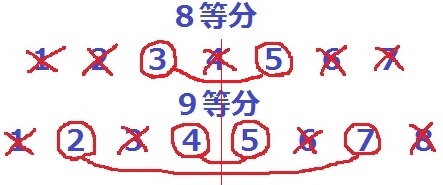
８等分と９等分はこのような感じになる。
つまるところ、半分だけを調べればいい。
１～12までのうち、１と12は×。
24と公約数をもつ数を消していくと５・７・11しかない。
よって、星形正二十四角形は３種類ある。
＠＠＠＠＠＠
では、先端部分の角が最も小さくなるときはどういう星形か？
角度が尖がる星型は、先端の角を円周角としたとき、それに対する弧が短い。
弧が短くなるのは、対称の軸である真ん中のラインに近いものである。
24等分であれば、11（と13）のペア。
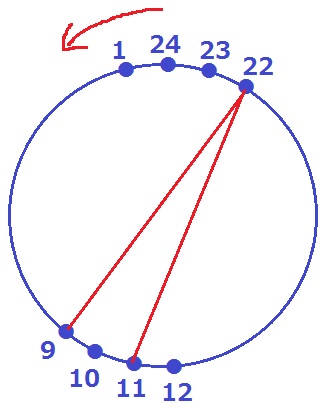
24番目から反時計回りに進むとする。11個目ずつに結ぶと…
11→22→９（＝22＋11－24）
弧は９番目と11番目、すなわち、弧２個分である。
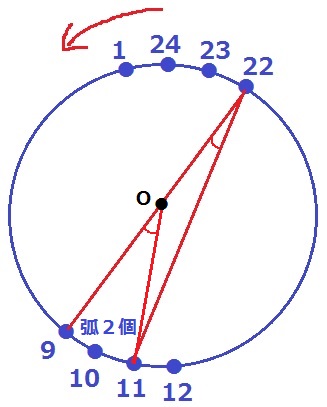
中心角は360×２/24で、この円周角だから半分にする。
先端部分の角は、360×２/24÷２＝15°
浅野中学でも星形多角形が出題されました。
大問１
（６）球の表面積、体積は覚えておこう！他のとこでも小問にでてくる。
（７）３本目の平行線でもできるが、延長でもいける。
大問２
解きやすかった。（３）中学受験の算数で解いた。
大問３
（２）ここで落とすのはもったいない。混乱したら三角形をちゃんと書く。
（４）四角錘の高さ＝円Ｏの半径→正三角形ＢＣＥの利用。
底面積の四角形は高さの比で対処。
大問４
（３）②反射の問題（線対称）と気づければ、正答率はもう少し上がったか。
大問５
（３）②ここらへんからバテる。。後回しがいいと思う。
前の組み合わせに×１を追加。ａ＝０を忘れないように。
大問６
対応力が試される。平面と整数が絡みあう。
（２）360°が⑦、２ｘが③に相当する。
（３）前問の図を利用。４個分のほうが固定なので、２ｘに相当するのはｎ－４個。
（４）なんでこっちのほうが正答率イイワケ？(‘ω’)
全部は試せないので規則をさぐる。約数を疑うこと。
後半は☆がウニみたいにチクチクするのはどういうときか。表を参照する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント