問題はコチラ→ＰＤＦファイル
2024大阪（数学）Ａ問題の解説はコチラ。
大問１（計算）
（１）
（－１）2－２×３
＝１－６
＝－５
（２）
３（ｘ－９ｙ）＋４（ｘ＋７ｙ）
＝３ｘ－27ｙ＋４ｘ＋28ｙ
＝７ｘ＋ｙ
（３）
２ｂ×６ａ2÷（－４ａ）
＝－３ａｂ
（４）
（ｘ＋３）（ｘ－３）－ｘ（ｘ－２）
＝ｘ2－９－ｘ2＋２ｘ
＝２ｘ－９
（５）
（√７＋２√２）2
＝７＋４√14＋８
＝15＋４√14
大問２（小問集合）
（１）
８ａ＋ｂ2
＝８×（－３）＋４2
＝－24＋16
＝－８
（２）
ａ＜０、ｂ＞０
迷ったら適当な値を代入して、反例を挙げればいい。
ア：ａｂ＝（－１）×１＝－１×
イ：ａ＋ｂ＝－２＋１＝－１×
ウ：－ａ＋ｂ＝－（－１）＋１＝２〇
－ａは正。正＋正だから必ず正になる。
エ：ａ－ｂ＝－２－１＝－３×
ウ
（３）
ｘ2－７ｘ＋５＝０
解の公式を適用して、ｘ＝（７±√29）/２
（４）
√（44ｎ）＝２√（11ｎ）
これが自然数となる最小のｎ＝11
（５）
取り出した２枚をＣ・Ｄとする。
ａ＝Ｃ＋Ｄ
ｂ＝Ｃ×Ｄ
ｂ－ａ＝Ｃ×Ｄ－（Ｃ＋Ｄ）＝偶数
差が偶数となるのは、（奇数－奇数）（偶数－偶数）のいずれか。
つまり、（Ｃ×Ｄ、Ｃ＋Ｄ）＝（奇数、奇数）（偶数、偶数）
●積和が（奇数、奇数）
Ｃ×Ｄ＝奇数となるのは、ＣとＤがともに奇数。
しかし、ともに奇数だとＣ＋Ｄ＝奇数＋奇数＝偶数となり不適。
●積和が（偶数、偶数）
Ｃ×Ｄ＝偶数は、（Ｃ、Ｄ）＝（奇、偶）（偶、奇）（偶、偶）
このうち、Ｃ＋Ｄも偶数になるのは（Ｃ、Ｄ）＝（偶、偶）しかない。
つまり、条件を満たすＣ、Ｄの組み合わせは２枚とも偶数である場合である。
偶数３枚から２枚選ぶ→選ばない１枚を選ぶ→３通り
全体は５枚から２枚選ぶ→5Ｃ2＝10通りだから、確率は３/10
（６）
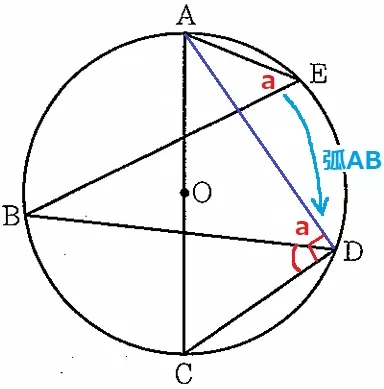
直径ＡＣに対する円周角から、∠ＡＤＣ＝90°
弧ＡＢに対する円周角から、∠ＡＤＢ＝ａ
∠ＢＤＣ＝90－ａ
（７）
抽出した30個のうち、赤：青＝26：４＝⑬：②
青は全部で80個なので、赤は80×⑬/②＝520個
（８）
答案では途中に式を含めた求め方も説明する。
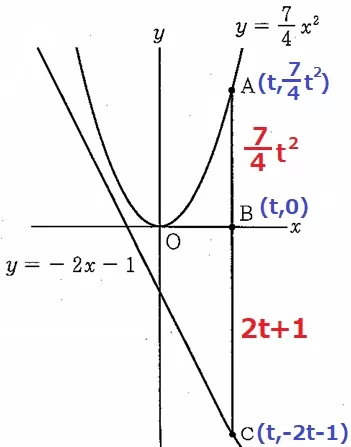
各座標をｔで用いて示すとこうなる。
ＡＢ＝７/４ｔ2
ＢＣの長さは－２ｔ－１ではない点に注意！
ＢＣ＝０－（－２ｔ－１）＝２ｔ＋１
ＢＣ＝ＡＢ＋１
２ｔ＋１＝７/４ｔ2＋１
７/４ｔ2－２ｔ＝０ ←４倍
７ｔ2－８ｔ
＝ｔ（７ｔ－８）＝０
ｔ＞０より、ｔ＝８/７
大問３（数量変化）
（１）①
ａ＝15の場合、初項が90、等差90＋15＝105の数列。
ｘ＝４のとき、ｙ＝90＋105×（４－１）＝405
ｘ＝７のとき、ｙ＝90＋105×（７－１）＝720
ア…405、イ…720
②
105ずつ増加→変化の割合（傾き）は105
（１、90）から左に１、下に105移動して、切片は90－105＝－15
ｙ＝105ｘ－15
③
先の式にｙ＝2085を代入する。
2085＝105ｘ－15
ｘ＝20
（２）
21枚の垂れ幕の長さは、90×21＝1890ｃｍ
間隔の合計は、2130－1890＝240ｃｍ
間隔は20ヵ所あるので、ａ＝240÷20＝12
大問４（図形）
Ⅰ（１）
△ＧＡＦ∽△ＦＢＣの証明。
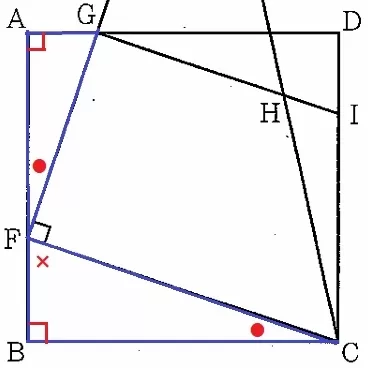
∠ＧＡＦ＝∠ＦＢＣ＝90°
∠ＡＦＧ＝180－∠ＧＦＣ－∠ＣＦＢ＝90－∠ＣＦＢ（×）
△ＦＢＣの内角より、∠ＢＣＦ＝180－∠ＦＢＣ－∠ＣＦＢ＝90－∠ＣＦＢ（×）
∠ＡＦＧ＝∠ＢＣＦ（●）
２角が等しいので∽。
（２）①
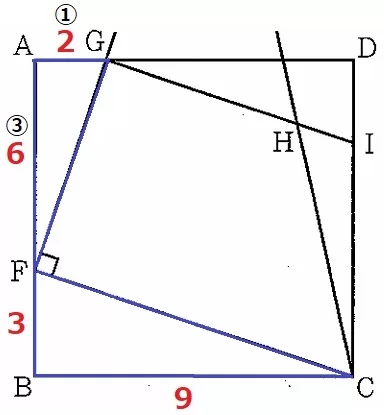
ＡＦ＝９－３＝６ｃｍ
前問の△ＧＡＦ∽△ＦＢＣを使う。
ＧＡ：ＡＦ＝ＦＢ：ＢＣ＝３：９＝①：③
ＡＧ＝６×①/③＝２ｃｍ
△ＧＡＦで三平方→ＧＦ＝２√10ｃｍ
②
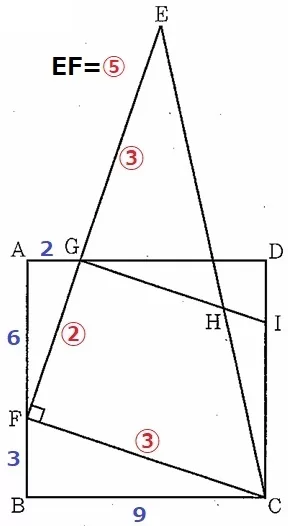
△ＧＡＦ∽△ＦＢＣの斜辺であるＧＦ：ＦＣ＝②：③とする。
仮定よりＥＦ：ＦＣ＝５：３なので、ＥＦ＝⑤
ＥＧ＝⑤－②＝③
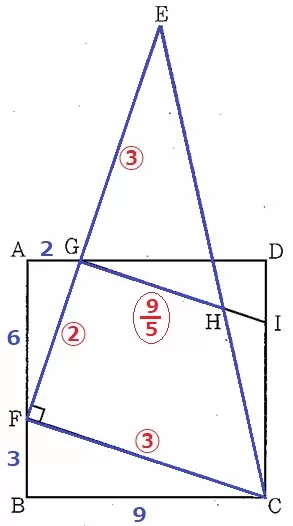
△ＥＧＨ∽△ＥＦＣより、ＥＧ：ＧＨ＝ＥＦ：ＦＣ＝５：３だから、
ＧＨ＝③×３/５＝〇９/５
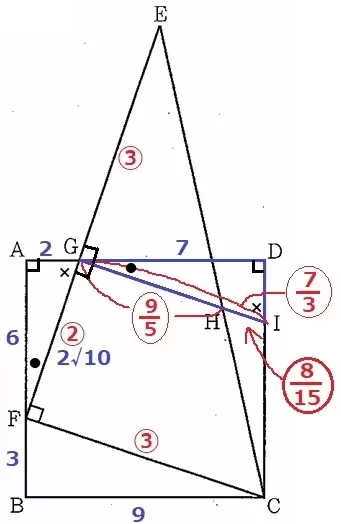
ＨＩ＝ＧＩ－ＧＨ
ＧＩを斜辺とする△ＩＤＧに着目する。
ＧＩ//ＦＣの同位角でＥＦ⊥ＩＧ→∠ＩＧＦ＝90°
●＋×＝90°で等角を移していくと、２角相等で△ＧＡＦ∽△ＩＤＧ
ＧＤ＝９－２＝７ｃｍ
ＧＩ＝②×７/６＝〇７/３
ＨＩ＝〇７/３－〇９/５＝〇８/15
ＧＦ：ＨＩ＝②：〇８/15＝15：４
ＨＩの長さは、２√10×４/15＝８√10/15ｃｍ
@別解@
他にも方法がないか調べてみました。
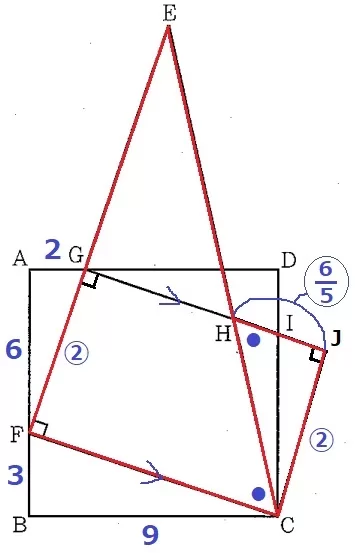
長方形ＧＦＣＪをつくる。
長方形の対辺は等しいので、ＪＣ＝②
△ＥＦＣ∽△ＣＪＨより、ＥＦ：ＦＣ＝ＣＪ：ＪＨ＝５：３
ＨＪ＝②×３/５＝〇６/５
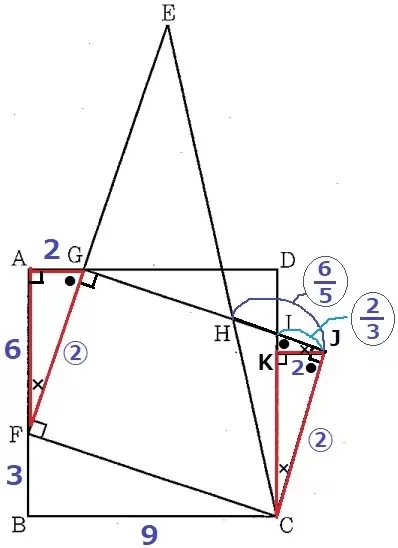
ＪからＤＣに垂線をおろし、交点をＫとする。
△ＧＡＦ≡△ＪＫＣ（斜辺ＧＦをＪＣに平行移動するイメージ）
ＫＪ＝ＡＧ＝２ｃｍ
●＋×＝90°で等角を調べていくと、２角相等で△ＧＡＦ∽△ＩＫＪ
ＩＪ＝②×２/６＝〇２/３
ＨＩ＝〇６/５－〇２/３＝〇８/15
ＧＦ：ＨＩ＝②：〇８/15＝15：４
ＨＩの長さは、２√10×４/15＝８√10/15ｃｍ
Ⅱ（３）
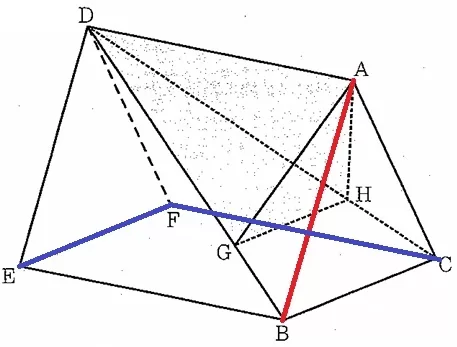
ねじれの位置→延長しても交わらない、かつ平行でもない。
辺ＡＢとネジレなのは辺ＥＦと辺ＣＦ。
ウ・エ
（４）①
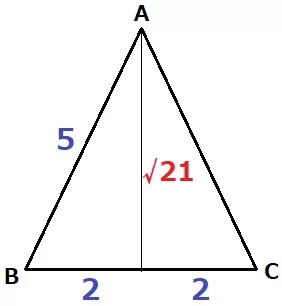
△ＡＢＣは二等辺三角形。
縦に分割して三平方を使うと、高さは√21ｃｍ
△ＡＢＣの面積は、４×√21÷２＝２√21ｃｍ2
②
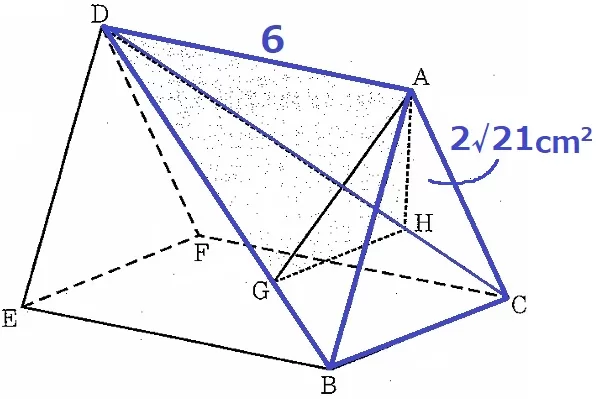
三角錐Ｄ―ＡＢＣの体積は、２√21×６÷３＝４√21ｃｍ3
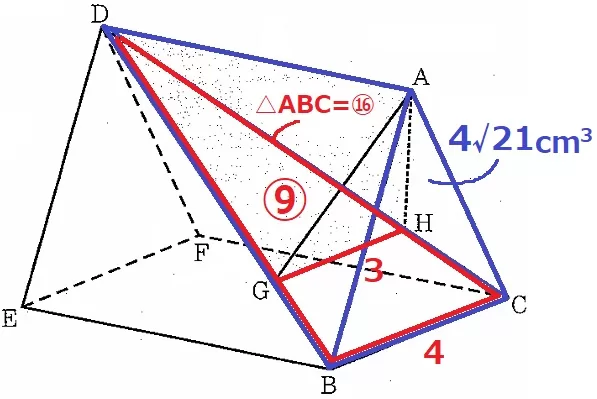
三角錐Ａ―ＤＢＣ：三角錐Ａ―ＤＧＨ＝△ＤＢＣ：△ＤＧＨ＝４2：３2＝⑯：⑨
三角錐Ａ―ＤＧＨの体積は、４√21×⑨/⑯＝９√21/４ｃｍ3
大問１
配点15点。すべて死守。
大問２
（２）文字で考えてみる→それでも迷ったら具体的な代入がいいかな。
（４）√44＝２√11に変え、√11の根号をなくすには何をかければいいか。
（５）差が出やすい。２数の積－２数の和＝偶数となる２数を偶奇判定で絞る。
（７）抽出した30個から赤：青の比を求め、青全部が80個だから赤全部も出る。
（８）ＢＣの長さの符号を注意しよう。
大問３
題材はＡ問題と共通。内容も解きやすい。
（２）算数で解ける。
大問４
Ⅰ（２）①前問の∽とＧＦの長さから、ＧＦ：ＨＩの比を出せないか。
対応する辺の比はＧＦ：ＦＣ＝②：③とおくと、ＥＧ＝③まで整数比になる。
ＥＧ→ＧＨとつながれば、ＧＩに目がいきやすいと思う。
ＧＩを１辺とする△ＩＤＧも●＋×＝90°で相似を指摘できる。
Ⅱ（４）②平面より空間の方がやりやすかった。
底面積の比で大きい三角錐の体積を案分する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント