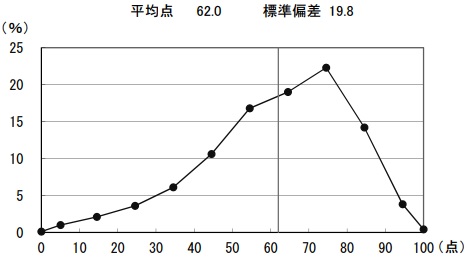
平均62.0点(前年比;+3.2点)
問題はこちら→リセマムさん
大問1(計算)-89.6%
(1) 97.3%
-10-(-4)
=-10+4
=-6
(2) 89.6%
6×(-2/3)2
=6×4/9
=8/3
(3) 95.8%
4(3x-2y)-5(x-2y)
=12x-8y-5x+10y ←10yの符号注意!
=7x+2y
(4) 83.4%
xy2÷2y×8x
=4x2y
(5) 86.9%
√3(√12+√6)
=√36+√18
=6+3√2
(6) 84.6%
2x2-3x-4 ←因数分解できないので解の公式
x={3±√(9+32)}/4
=(3±√41)/4
大問2(小問集合)-62.7%
(1) 85.6%
ねじれの位置→延長しても交わらない&平行でない
ABとねじれの位置にあるのは、EH・FG・DH・CG。
イ
(2) 55.1%
半球の体積。
球の体積:4/3πr3
4/3π・63=144πcm3
(3) 50.0%
変化の割合=(yの増加量)/(xの増加量)
-4=(62・a-22・a)/(6-2)=32a/4
8a=-4 a=-1/2
@別解@
y=ax2のグラフで、xの値がpからqまで増加するときの変化の割合は、a(p+q)
(2+6)a=-4
8a=-4
a=-1/2
(4) 71.7%
6の倍数ということは、(2の倍数)×(3の倍数)
Aのカードで場合分け。
〔Aで1・5・7をとる〕→Bで6をとるしかない。各1通り
〔Aで3・9をとる〕→3と9は3の倍数。Bで2の倍数をとればいい。
Bは全て偶数だから全部あてはまる。各4通り
全部で11通り
カードの取出しからは5×4=20通り
確率は11/20
(5) 6点-51.2% 3点-5.5% 無答-16.1%
荒ぶる作図が千葉数学のアイデンティティの1つだったのに、
今年度は前期・後期ともに普通の問題に。。
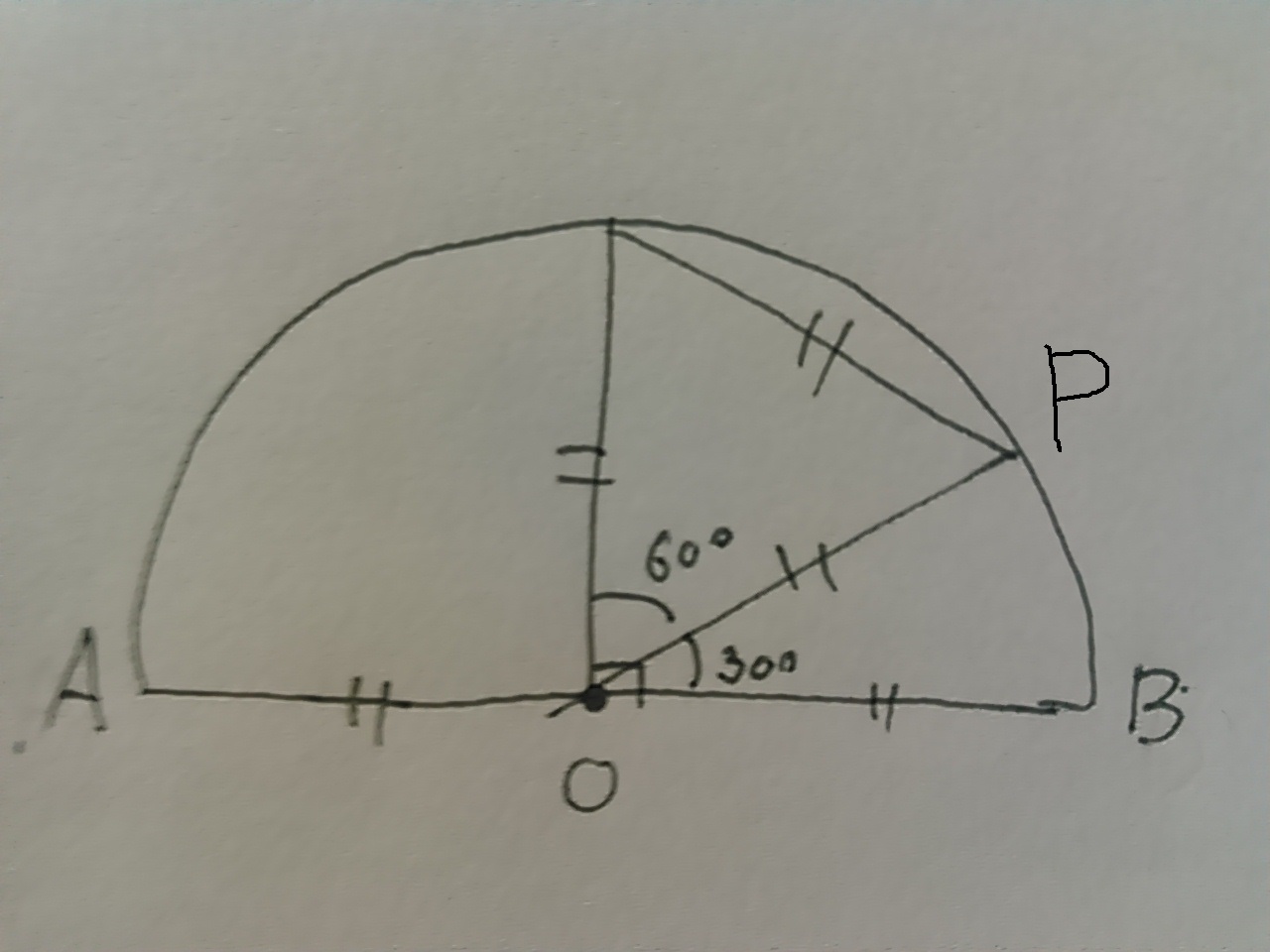
①ABの垂直二等分線
②半径をもとに正三角形を作成。
これで ∠POBが30°となります。 特筆すべき事項はないので、作図手順は省略。
大問3(関数)-50.0%
(1) 87.4%
Aの座標が判明しているので、y=ax2に代入する。
1=(-2)2 a
4a=1
a=1/4
(2) 56.9%
OCの式:O→Cが右に6、上に9なので、傾きは9/6=3/2
これと平行なので、傾きは3/2
B座標は、y軸を中心にA座標を対称移動したもの→B(2、1)
y=ax+bに代入
1=2×3/2+b
b=-2
y=3/2x-2
(3) 5.6%!!
定石としては、(2)の誘導からOCと平行になるよう、
AとBをx座標に落とし、その中点とCを通る直線を求めるところだが、
処理手順が多く、計算も面倒くさい・・。
後期は時間勝負なので、別の手を考えてみる。
求めたいのは、『2等分する直線とOAとの交点』なので、
2等分する直線がOAを通過することから、
四角形OBCA内部の面積比で2等分線が辺OAのどこを内分するかを考える。
まずは、四角形OBCAの求積。
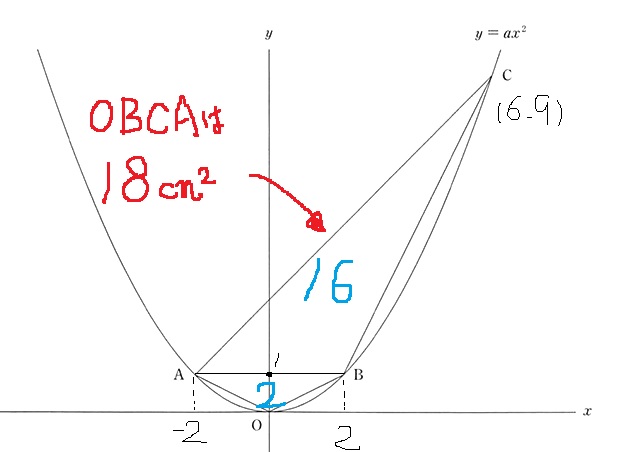
ABを結ぶとx軸に平行な直線となる。
AB=4
3つの点座標から下が2cm2、上が16cm2
あわせて18cm2となる。
ということは、2等分すると9cm2ずつに分かれる。
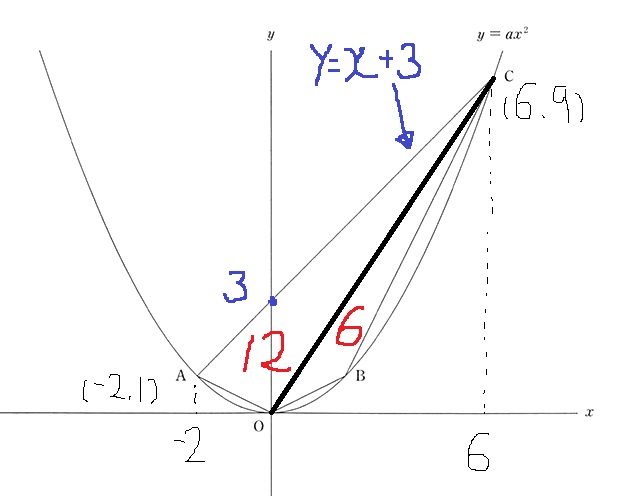
△CAOの求積。
直線ACは、右に8、上に8なので傾きは1
式はy=x+3
お馴染みの等積変形でAとCをx座標に下ろす。
△CAO=8×3×1/2=12cm2
△COBは6cm2となる。
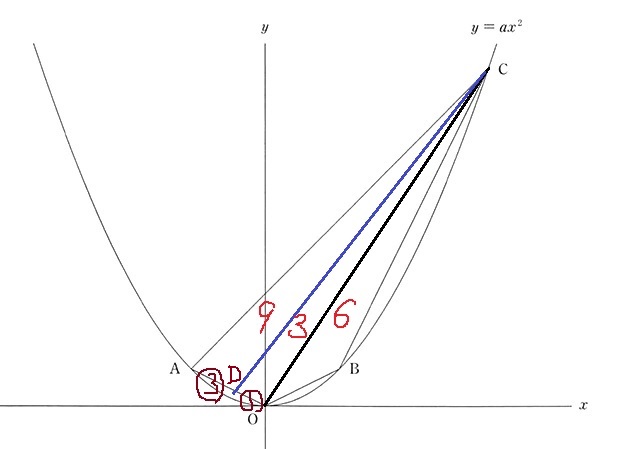
青い線が四角形OBCAを2等分する直線。
これとOAとの交点をDとおく。
△COBが6cm2なので、△CAD:△CDO=9:3=3:1
AD:DO=3:1
A(-2、1)なので、Dのx座標は、-2×1/4=-1/2
OA;y=-1/2xなので、
D(-1/2、1/4)
複雑な四角形は等積変形だけでなく、
四角形内部の面積比から内分点の位置を探る。
大問4(平面図形)-53.6%
(1)
はじめは、△BCE≡△CBFの証明。
a・・2つの三角形に注目して、対応する角を選ぶ。
∠CBE=∠BCF → ウ 96.1%
b・・2本と辺と間の角度の話 → オ 91.8%
c・・6点-9.4%! 3点-3.8% 無答-42.6%!
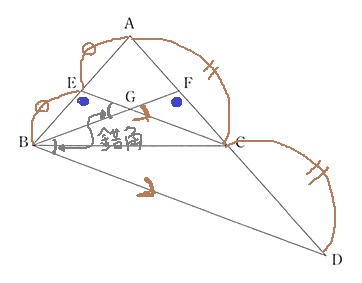
中点連結定理を使う。
EC//BDから錯角
青丸は前問の合同から。
2角が等しい→∽
(2) 17.0%!
いつもは悩みポイントなのに、例年と比べればここもやりやすくなっている。
BE=①とおく。
合同からFC=①
FはACの中点だから、AF=②
CはADの中点だから、CD=②
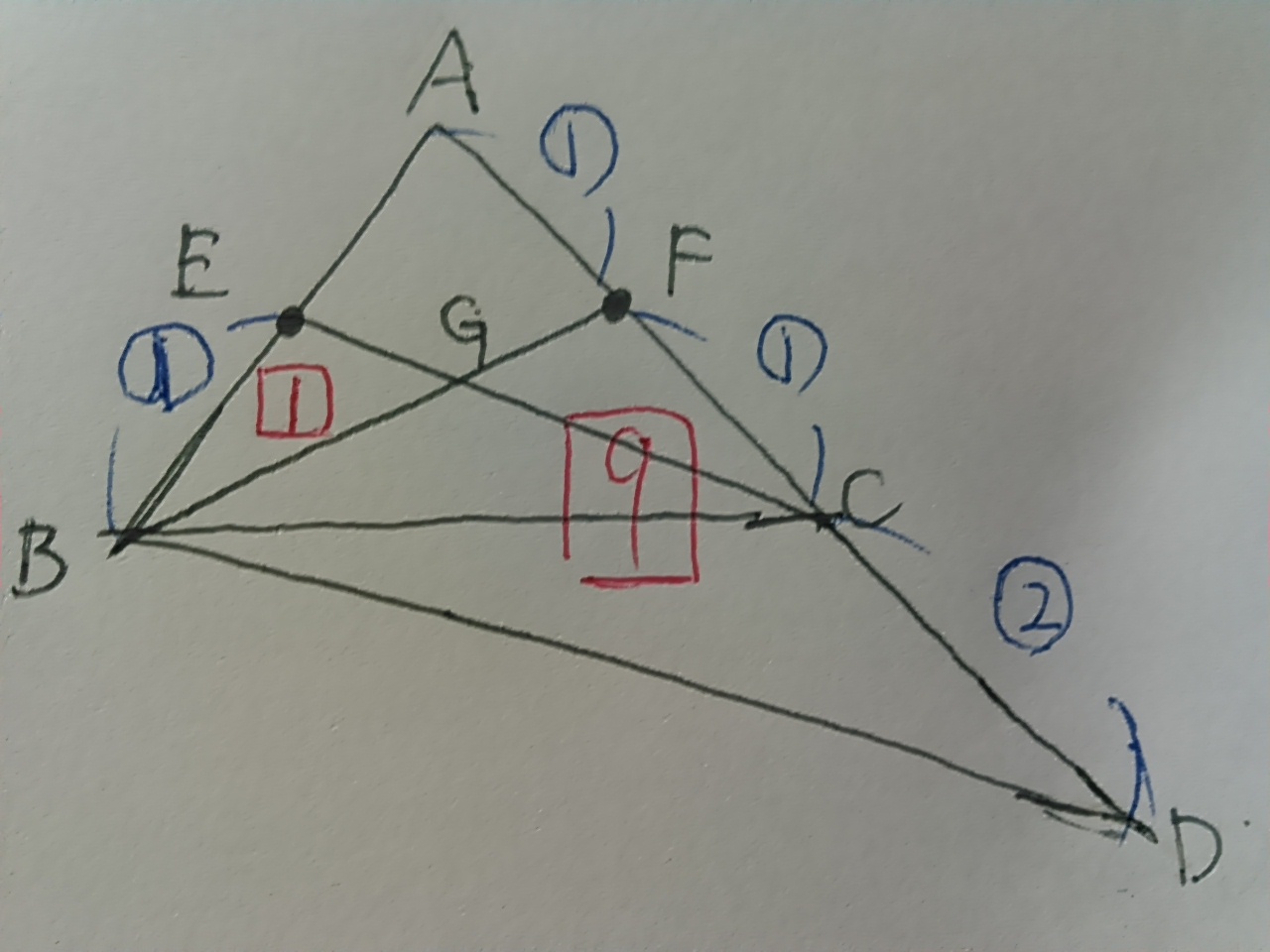
△BEGの面積を□1とおくと、
面積比から、△FBDは③×③で□9
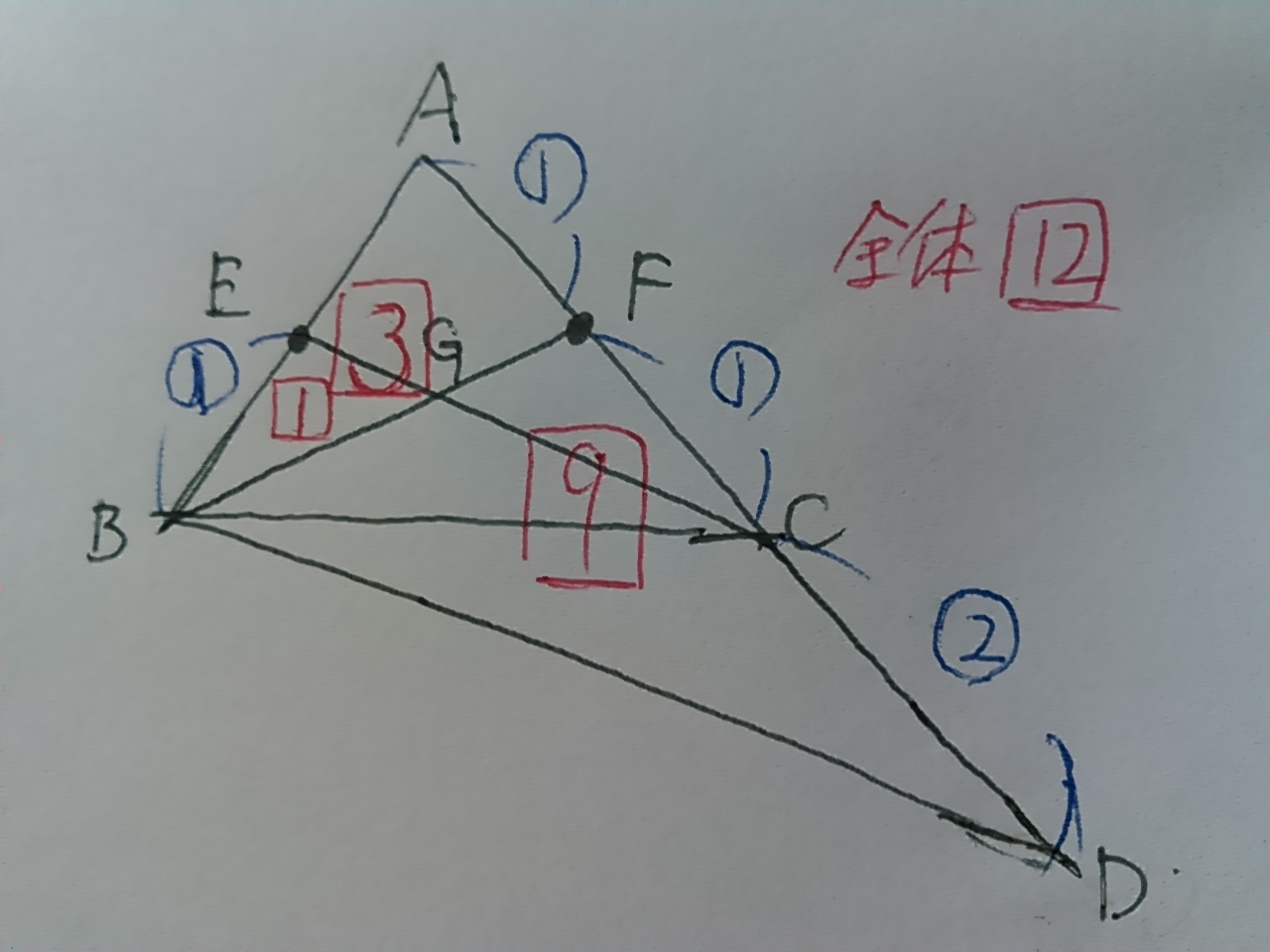
AF:FD=1:3だから、辺AD方向からみて△ABFは□3
△ABD全体の面積は□12
△BEGが1cm2だから、△ABDは12cm2
大問5(整数)-54.1%
中学入試の算数(約束記号)。ルールに従って、整数を丁寧に処理できるか否か。
中学受験を経験していないと、真新しく感じるかもしれません。
(1) 93.4%
37÷7=5・・2
(ア)=5 (イ)=2
(2) 62.1%
[a☆7]=7を式で表すと、
a÷7=7…(余り0~6)
余りは割る数7より小さい。割り切れたら余りは0。
答えは7個
*数でいえば、49~55の7個です。
(3) 41.0%
[a☆14]=3・・①、 [a◎7]=3・・②
同様に式で表してみる。
①:a÷14=3…(余り0~13)←(余りは割る数未満)
②:a÷7=□…3
①から、aの範囲は42~55
②のaを言葉で表すと、[7の倍数+3]
42が7の倍数なので、+3して45
7の倍数+3である45に+7をすれば、その数も7の倍数+3。
45+7=52
45と52
(4) 19.7%!
[a◎3]=1・・①、 [a◎4]=3・・②
これらの式を言葉で表すと、
①:aは3で割って余りが1となる→〔3の倍数+1〕
②:aは4で割って余りが3となる→〔4の倍数+3〕
こういうときは、試しに書いてみる。
①:1、4、7、10、13、16、19、22・・
②:3、7、11、15、19、23、27・・
7を起点に(3と4の最小公倍数である)12ごとで共通した数が表れる。
7、19、31、43、55、67、79、91、103・・
2桁の自然数aは7個
*約束記号はとりあえず式で表す。『式を日本語に言語化してみる』とわかりやすい。



コメント