2021年度　青森県公立高校入試問題過去問【数学】解説

平均56.2点（前年比；＋1.5点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア　97.9％
－１－５
＝－６

イ　94.0％
（－３）²＋４×（－２）
＝９－８＝１

ウ　76.8％
10ｘｙ²÷（－５ｙ）×３ｘ
＝－６ｘ²ｙ

エ　66.1％
２ｘ－ｙ－（５ｘ＋ｙ）/３　←すべてを分母３に巻き込む。
＝（６ｘ－３ｙ－５ｘ－ｙ）/３
＝（ｘ－４ｙ）/３

オ　77.9％
（√５＋３）（√５－２）
＝５＋√５－６
＝－１＋√５

（２）　75.2％
ℓ＝２πｒ　←左右入れ替え
２πｒ＝ℓ　←両辺を÷２πｒ
ｒ＝ℓ/(２π)

（３）　54.7％
ｘ²＝９ｘ
ｘ²－９ｘ
＝ｘ（ｘ－９）＝０
ｘ＝０、９

（４）　79.1％
ｙ＝ａｘに、（ｘ、ｙ）＝（－３、18）を代入。
18＝－３ａ
ａ＝－６

ｙ＝－６ｘに、ｘ＝１/２を代入。
ｙ＝－６×１/２＝－３

（５）　56.9％
１つの外角は、180－140＝40°
多角形の外角の和は360°だから、
ｎ＝360÷40＝９

（６）　28.3％！
ア：３点は一直線に含まれるので、一直線と面の関係性を考える。

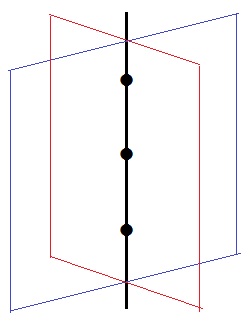
一直線を軸にすると、面をクルクル回せる→１つの面に定まらない。ア

他は面をクルクル回せない。

（７）　46.3％
14人の中央値（48.0回）は７番目と８番目の平均。
この差が６回だった。

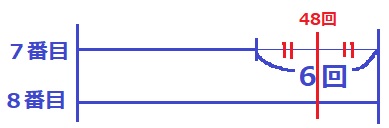
７番目は、48－（６÷２）＝45回

（８）　12.7％！

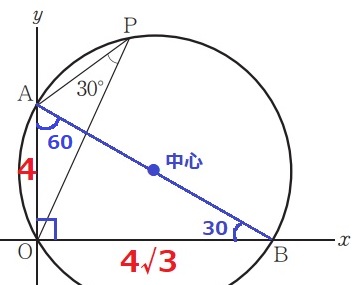
円の中心は直径の中点。
直径になりそうな線分ＡＢをひいてみる。

∠ＡＯＢ＝90°
直径に対する円周角は90°→直角三角形の斜辺ＡＢは円の直径。

円周角の定理より、∠ＡＢＯ＝∠ＡＰＯ＝30°
△ＯＡＢの内角は30°—60°—90°で辺の比は１：２：√３。
ＯＢ＝４√３
円の中心の座標は、（４√３÷２、４÷２）＝（２√３、２）

大問２（整数＆確率）

（１）ア92.2％、イ78.0％、ウ～オ66.7％
偶数＋偶数＝偶数の証明。
異なる２つの偶数は２ｍ、２ｎとすると、
２ｍ＋２ｎ
＝２（ｍ＋ｎ）
ｍ＋ｎは自然数だから、２（ｍ＋ｎ）は偶数。

後半は、偶数×偶数が８の倍数にはならない例を示す。
２×６＝12
６×10＝60
14×18＝252
４の倍数ではない偶数の組み合わせであればなんでも良い。
２ｍ×２ｎ
＝４ｍｎ　←４の倍数までしか証明できない。
ア…ｍ＋ｎ、イ…偶数、ウ…２、エ…６、オ…12（ウエオは一例）

（２）ア　65.1％
それぞれの袋で白を出す確率は２/６＝１/３
１/３×１/３＝１/９

イ　43.6％
最も起こりやすい事象→結果の数が最も多い。
どちらも赤…１×１＝１通り
どちらも白…２×２＝４通り
どちらも黒…３×３＝９通り
赤１と白１…異色の場合、袋を逆にしたパターンもある！１×２×２＝４通り
白１と黒１…２×３×２＝12通り
赤１と黒１…１×３×２＝６通り
最も起こりやすいのは、白１と黒１（お）

大問３（図形）

（１）ア　50.5％

３×４÷２×６÷３＝12ｃｍ³

イ　34.9％
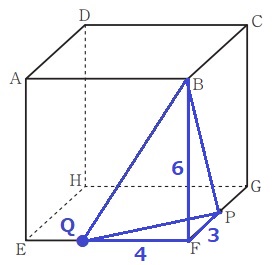
展開図を描いてＰＲを一直線にする。

角度がやらしいが(;´Д｀)、ＥＦを真ん中にパカっと開く。
ＰとＲはともに辺の中点なので、ＰＲを斜辺とする直角三角形は、
等辺が６ｃｍの直角二等辺三角形となる。
辺の比は１：１：√２→ＰＲ＝６√２

（２）ア　あ52.5％、い58.8％、う66.8％
△ＢＣＤ≡△ＡＣＥの証明。難しくない。

△ＡＢＣと△ＤＣＥは正三角形。
ＢＣ＝ＡＣ，ＣＤ＝ＣＥ、∠ＢＣＤ＝∠ＡＣＥ＝60°
２辺と間の角がそれぞれ等しいので、△ＢＣＤ≡△ＡＣＥ
あ…ＢＣ＝ＡＣ、い…∠ＢＣＤ＝∠ＡＣＥ、う…２辺と間の角
（*対応する順にアルファベットを並べること！
△ＢＣＤ→△ＡＣＥに関する情報の順で書いた方が望ましい）

イ（ア）　32.3％！

周りの長さ（赤線）が21ｃｍ。
ＡＥ＝21－２ａ－ｂ

（イ）　19.2％！
前問の解答を活用する。

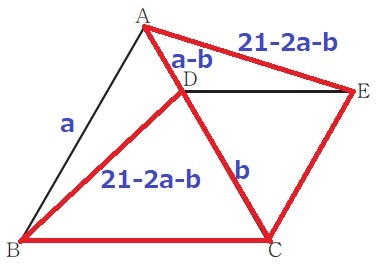
（２）△ＢＣＤ≡△ＡＣＥより、対応する辺からＢＤ＝ＡＥ＝21－２ａ－ｂ
ＡＤ＝ＡＣ—ＤＣ＝ａ－ｂ

△ＡＢＤの周の長さは13ｃｍだから、
ａ＋（ａ－ｂ）＋（21－２ａ－ｂ）＝13
21－２ｂ＝13
ｂ＝４
正三角形ＤＣＥの１辺の長さは４ｃｍ。

大問４（関数）

（１）　52.5％
ｙ＝－４/９ｘ²にｙ＝－４を代入。
－４/９ｘ²＝－４
ｘ²＝９
Ｂのｘ座標は負の値（ｘ＜０）だから、ｘ＝－３

（２）　59.2％
ｘ＝３のとき、ｙ＝－４
ｘ＝６のとき、ｙ＝－16
変化の割合＝（ｙの増加量）÷（ｘの増加量）
＝｛－16－（－４）｝÷（６－３）＝－４

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑまで増加するときの変化の割合はａ（ｐ＋ｑ）。
－４/９×（３＋６）＝－４

（３）　19.6％！

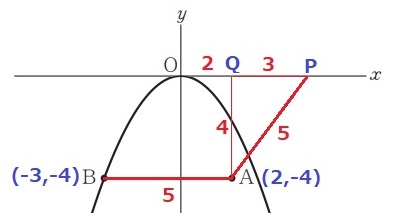
ＡＢの長さは、２－（－３）＝５
Ｐのｘ座標が正となるようにＡＰを描く。（ＰはＡより右側にある）

Ａからｘ軸に向けて垂線ＡＱを引く。
△ＡＰＯに注目すると、ＡＰ＝５、ＡＱ＝４だから、
辺の比が３：４：５の直角三角形→ＰＱ＝３
Ｐ（５、０）

（４）　7.6％!!

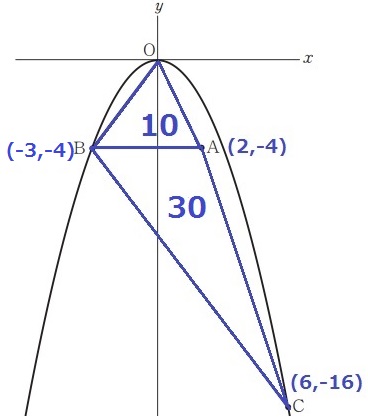
Ｃ（６、－16）
四角形ＯＢＣＡをＡＢで分ける。
座標の距離から２つの三角形の面積を調べる。
△ＯＡＢ＝５×４÷２＝10
△ＡＣＢ＝５×12÷２＝30
四角形ＯＢＣＡの面積は40だから、20ずつにすれば半分になる。

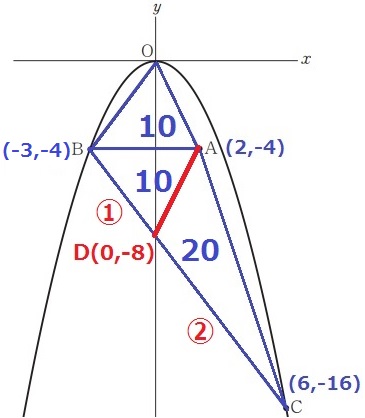
四角形ＯＢＣＡを二等分する線をＡＤとする。
ＢＤ：ＤＣ＝△ＡＤＢ：△ＡＣＤ＝10：20＝①：②
ＢＣを１：２に内分する。
ｘ座標は、－３＋９×①/③＝０
ｙ座標は、－４－12×①/③＝－８
Ｄ（０、－８）
Ｄはちょうどｙ軸上にある。

Ｄ（０、－８）⇒Ａ（２、－４）
右に２、上に４だから、傾きは２。
ＡＤ；ｙ＝２ｘ－８

大問５（数量変化）

（１）あ85.8％、い84.5％、う66.2％
縦の１目盛りは500ｍ。バス停までは1500ｍ。
マユは出発してから20分後～29分後の９分間、バスを待っている。
バスの速さは右２マス、縦３マスの傾きだから、1500ｍ÷２分＝分速750ｍ
あ…1500、い…９、う…750

（２）ア　46.9％

兄の移動時間は、12000ｍ÷分速250ｍ＝48分間
マユが出発してから７～55分後。（０、７）と（55、12000）を結ぶ。

イ　38.4％

先ほどのグラフで、マユと兄の距離が最も長いのは午前10時29分。
兄は分速250ｍで２分おきに格子点を通る。縦８目盛り分なので、500×８＝4000ｍ
午前10時29分、4000ｍ

（３）　31.7％
これが最後の問題なのか(･Д･)??
マユは午前10時43分、兄は午前10時55分に博物館に着く。
兄は12分遅れで到着、７分遅れで出発している。
ということは、マユの５分前に出発すればいい。
午前９時55分