2021年度　埼玉県公立高校入試問題過去問【数学】解説

平均62.2点（前年比；－5.7点）

問題はコチラ→ＰＤＦファイル
学校選択問題の解説はコチラ。
出題範囲の除外は円周角と中心角、三平方の定理、標本調査、実生活で相似を活用する問題。

大問１（小問集合）

（１）　97.0％
４ｘ－９ｘ
＝－５ｘ

（２）　90.8％
－３＋（－４）×５
＝－３－20
＝－23

（３）　77.6％
４ｘｙ÷８ｘ×６ｙ
＝３ｙ²

（４）　88.2％
３ｘ＋２＝５ｘ－６
２ｘ＝８
ｘ＝４

（５）　80.6％
２√３－15/√３
＝２√３－５√３
＝－３√３

（６）　90.1％
ｘ²＋７ｘ－18
＝（ｘ－２）（ｘ＋９）

（７）　80.6％（一部正答3.3％）
５ｘ－４ｙ＝９　…①
２ｘ－３ｙ＝５　…②
①×２－②×５をすると、７ｙ＝－７
ｙ＝－１
②に代入。２ｘ＋３＝５
ｘ＝１
ｘ＝１、ｙ＝－１

（８）　79.3％
２ｘ²－５ｘ＋１＝０
解の公式を適用して、
ｘ＝（５±√17）/４

（９）　75.0％

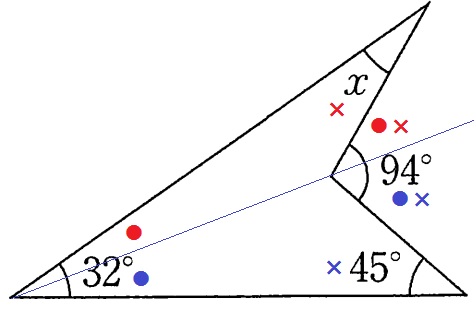
外角定理より、ブーメランの３つの角の和は股の角。
32＋ｘ＋45＝94
ｘ＝17°

（10）　50.3％
ｙの変域が０以下なので、上に凸のグラフ。
ｘ＝３のとき、最小値ｙ＝－36
ｙ＝ａｘ²は（３、－36）の点を通過するから、
－36＝３²ａ
ａ＝－４

（11）①　43.1％
【球の体積Ｖ＝４/３πｒ³】
Ｖ＝４/３π×２³＝32/３πｃｍ³

②　47.0％
【球の表面積Ｓ＝４πｒ²】
Ｓ＝４π×２²＝16πｃｍ²

（12）　90.1％

底面をどこかに定める。ア・エのように、横に並ぶ場合は２個先が平行な面。
残りは接する辺に合わせるように面を回転させて判断する。
イ

（13）　17.8％！（一部正答0.7％）
公立高校入試で有効数字はめずらしい。
整数部分が１桁だから、12700の最高位である１を１の位に置き換える。
→小数点は１と２の間にくる。
1.27×10000
10の累乗を指数を使ってあらわす。
1.27×10⁴
ア…1.27、イ…４

（14）　78.6％
ア：『同様に確からしいもの』は、あくまでも可能性。
イ：そんなワケあるか(´ﾟдﾟ｀)
ウ：そんなワケあるか(´ﾟдﾟ｀)
エ：３以下は１/２、４以上も１/２。確率は同じ。
エ

（15）　45.7％
40人の中央値（メジアン）は20番目と21番目の平均。
→６～８時間の階級に含まれる。
14÷40＝0.35

（16）　11.8％！（一部正答10.2％、無答40.8％!!）
説明問題。
図を利用する。各々の長さを求めて比べればいい。

端っこにある扇形を集めると１つの円になる。
アとイは直線部分で違いが出る。
差は、８×２－４×３＝４ｃｍ

大問２（作図・関数）

（１）　73.7％（一部正答3.9％）

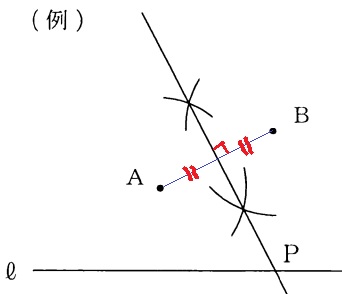
教科書レベルです。
『２点Ａ、Ｂから等距離にある』→ＡＢの垂直二等分線上のどこか。
これと直線ℓとの交点がＰ。

（２）　39.8％
ここも難しくはない。

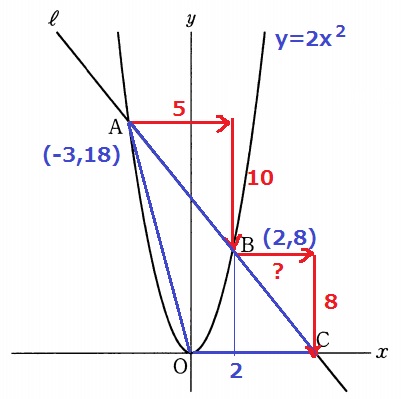
ｙ＝２ｘ²に代入して、Ａ（－３、18）Ｂ（２、８）
Ｃのｘ座標が知りたい。
Ａ→Ｂは左に５、下に10移動。（傾き－２）
Ｂ→Ｃは下に８さがるので、左に４移動する。
Ｃのｘ座標は２＋４＝６→Ｃ（６、０）
△ＡＯＣの面積は、６×18÷２＝54ｃｍ²

大問３（整数）

（１）ア　79.3％（一部正答5.9％）
４で割ると１余る数⇒４の倍数＋１
１、５、９、13…
13

イ
３ｘ＋5にｘ＝13を代入するだけ。
３×13＋５＝44

（２）①　7.2％!!（一部正答20.4％、無答31.3％）
４で割ると１余る自然数をｎ（０以上の整数）で表す。
４ｎ＋１
（*ｎ＝０、１、２、３…を代入すると、値は１、５、９、13…になる）

②
説明問題。
最後の１文に書かれてある内容をそのままやり遂げればいい。

３ｘ＋５のｘに４ｎ＋１を代入すると、
３（４ｎ＋１）＋５
＝12ｎ＋８
＝４（３ｎ＋２）
３ｎ＋２が整数だから、４（３ｎ＋２）は４の倍数である。

大問４（平面図形）

（１）　40.8％（一部正答25.7％）
△ＡＢＣ∽△ＡＣＤの証明。

共通角で∠ＢＡＣ＝∠ＣＡＤ
あとは問題文の∠ＡＢＣ＝∠ＡＣＤを写生。
２角が等しく∽。

（２）　53.3％

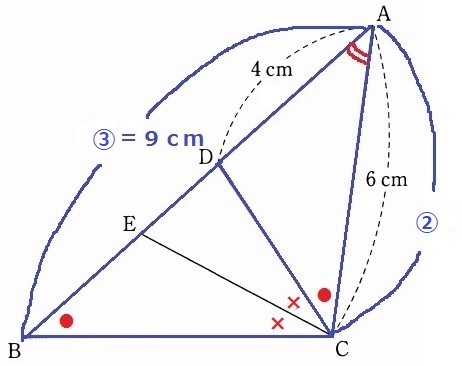
前問の△ＡＢＣ∽△ＡＣＤを利用する。
ＡＢ：ＡＣ＝ＡＣ：ＡＤ＝６：４＝③：②
ＡＢ＝６×③/②＝９ｃｍ

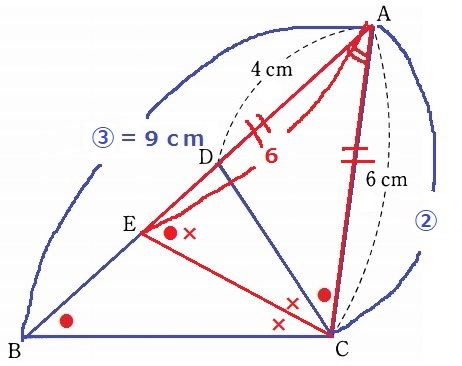
△ＢＣＥで外角定理→∠ＡＥＣ＝●×
△ＡＥＣの底角が●×で等しく、二等辺三角形である。
ＡＥ＝６ｃｍ
ＢＥ＝９－６＝３ｃｍ

＠別解＠

ＡＢ＝９ｃｍまでは先ほどと同様。
ＢＤ＝９－４＝５ｃｍ
△ＡＢＣ∽△ＡＣＤの辺の比で、ＢＣ：ＣＤ＝③：②
角の二等分線の定理で、ＣＤ：ＣＢ＝ＤＥ：ＥＢ＝【2】：【3】
ＢＥ＝５×【3】/【5】＝３ｃｍ
*公立高校入試対策でも角の二等分線の定理はおさえておくべきです。

（３）　1.6％!!（無答38.2％）

角の二等分線の定理から、ＡＢ：ＡＣ＝ＢＦ：ＦＣ＝９：６＝③：②
どうしても角の二等分線の定理を使いたくない人は、
△ＡＢＧと△ＡＣＧの高さの比からＢＦ：ＦＣ＝③：②と出しましょう。

二等辺ＡＥＣにおいて、頂角の二等分線は底辺ＥＣを垂直に二等分する。
ＥＧ＝ＧＣ
【△ＡＢＣ⇒△ＥＢＣ⇒△ＧＢＣ⇒△ＧＦＣ】
18×３/９×１/２×②/⑤＝６/５ｃｍ²

＠別解＠

ＥＧ＝ＧＣより、△ＡＢＧと四角形ＡＧＢＣは９ｃｍ²

ＡＥ：ＥＢ＝２：１から、△ＡＧＣ：△ＢＧＣ＝２：１
△ＡＧＣ＝６ｃｍ²、△ＢＧＣ＝３ｃｍ²

△ＡＢＧ：△ＡＣＧ＝３：２より、ＢＦ：ＦＣ＝③：②
△ＧＦＣ…３×②/⑤＝６/５ｃｍ²
中学受験の世界では『ベンツ切り』というそうな( ´д)ﾋｿ(´д｀)ﾋｿ(д｀ )