2022年度　大阪府公立高校入試Ａ問題過去問【数学】解説

平均58.2点（前年比；＋7.5点）
問題はコチラ→ＰＤＦファイル
2022年度・大阪（数学）Ｂ問題、Ｃ問題の解説はコチラ。

大問１（計算）

（１）　61.7％
－２－（－12）
＝－２＋12
＝10

（２）　59.4％
27×（－５/９）
＝－15

（３）　65.8％
40－７²
＝40－49
＝－９

（４）　35.8％
ｘ－３＋６（ｘ＋１）
＝ｘ－３＋６ｘ＋６
＝７ｘ＋３

（５）　52.5％
48ｘ³÷８ｘ
＝６ｘ²

（６）　44.2％
√12＋９√３
＝２√３＋９√３
＝11√３

大問２（小問集合）

（１）　35.0％
－２ａ＋14
＝－２×（－６）＋14
＝12＋14
＝26

（２）　38.3％
Ａ市の最低気温－Ｂ市の最低気温
＝5.3－（－0.4）
＝5.3＋0.4
＝5.7℃

（３）　50.8％
１袋にａ個のミカン。３袋だからミカンの合計は３ａ個。
これが20個より多いので、３ａ＞20
イ

（４）　33.1％！
７ｘ＋ｙ＝19　…①
５ｘ＋ｙ＝11　…②
①－②で、２ｘ＝８
ｘ＝４
②に代入して、５×４＋ｙ＝11
ｙ＝－９
ｘ＝４、ｙ＝－９

（５）　20.6％！
ｘ²－８ｘ＋15
＝（ｘ－３）（ｘ－５）＝０
ｘ＝３、５

（６）　50.8％
７人の中央値は、（７＋１）÷２＝４番目の値
28回

（７）　30.0％！
２枚のカードを取り出す→３×３＝９通り
積が16の組み合わせは、（２、８）（４、４）の２通り。
確率は２/９

（８）　26.7％！

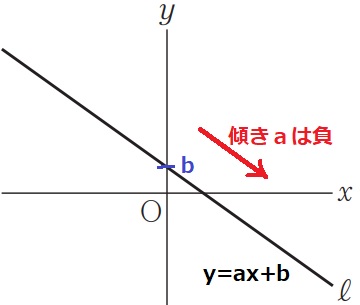
右下のグラフなので、傾きａは負。
切片ｂはｙ＞０だから正。
ウ

（９）　16.7％！
ｙ＝ａｘ²に（ｘ、ｙ）＝（－６、７）を代入して、
７＝36ａ
ａ＝７/36

（10）①　80.0％

ＡＣ//ＤＦ
エ

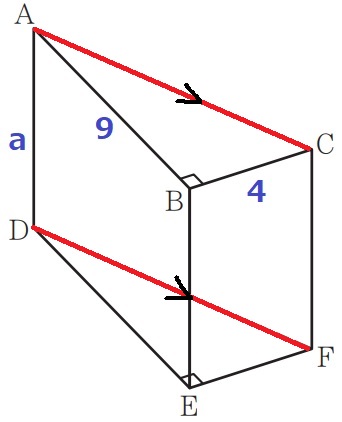
②　8.3％!!
柱の体積は【底面積×高さ】
三角柱ＡＢＣ—ＤＥＦの体積は、４×９÷２×ａ＝18ａｃｍ³

大問３（関数）

（１）①ア…75.8％、イ…49.2％

ｙの値は15ずつ増える。
15が増える回数はあいだの数、すなわち、（ｘ－１）回である。
ｘ＝４のとき、320＋15×（４－１）＝365
ｘ＝７のとき、320＋15×（８－１）＝425
ア…365、イ…425
＠＠
イはアから計算して、365＋15×（８－４）＝425でも良い。

②　10.0％!!
規則を一般化する。
ｙの値は、320に（ｘ－１）回分の15を足す。
ｙ＝320＋15（ｘ－１）＝15ｘ＋305
ｙ＝15ｘ＋305

（２）　28.3％！
ｙ＝15ｔ＋305にｙ＝620を代入する。
620＝15ｔ＋305
ｔ＝21

大問４（平面図形）

（１）　9.4％!!

△ＡＢＥの内角で、∠ＢＥＡ＝ａ°、∠ＡＢＥ＝90°だから、
∠ＢＡＥ＝180－（ａ＋90）＝90－ａ°

（２）　10.8％！
△ＨＤＦは正方形の半分→直角二等辺三角形。
辺の比は１：１：√２だから、ＦＤ＝５√２ｃｍ

（３）ａ…40.8％、ｂ…47.5％、ｃ…36.7％
△ＤＥＣ∽△ＩＤＧの証明。

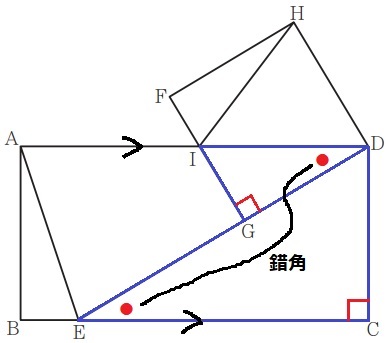
長方形ＡＢＣＤの内角より、∠ＤＣＥ＝90°
正方形ＦＧＤＨの内角より、∠ＩＧＤ＝90°
ＡＤ//ＢＣの錯角で、∠ＤＥＣ＝∠ＩＤＧ
２角が等しいから∽。
ａ…ＩＧＤ、ｂ…ＩＤＧ、ｃ…ウ

（４）　1.6％!!
答案では途中式を含めた求め方も書く。

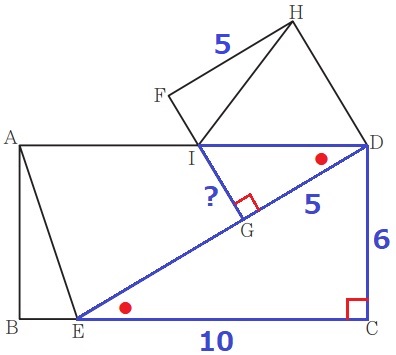
ＨＩのような斜線を求めるには、それを斜辺とする直角三角形で三平方を疑う。
直角三角形ＨＩＦに着目する。
正方形の１辺からＦＨ＝５ｃｍなので、ＦＩの長さが知りたい。
ＦＩを求めるには、ＩＧがわかればいい。

ＩＧは△ＩＤＧの辺。
ここで前問の△ＤＥＣ∽△ＩＤＧを用いる。
ＥＣ：ＤＧ＝ＤＣ：ＩＧ＝２：１
ＩＧ＝６÷２＝３ｃｍ

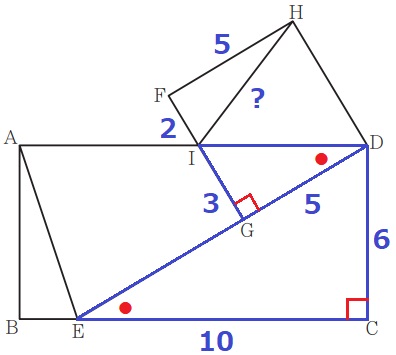
ＦＩ＝５－３＝２ｃｍ
△ＨＩＦで三平方→ＨＩ＝√29ｃｍ
公立高校入試解説ページに戻る