平均49.2点（前年比；－9.8点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
５/４ａ2÷15/２ａ
＝１/６ａ
（２）
２乗して６になる数が６の平方根。
負の数もある点に注意！
*－√６×（－√６）＝６
±√６
（３）
（ｘ－２）2＋（ｘ－２）（ｘ－４）＝０
ｘ2－４ｘ＋４＋ｘ2－６ｘ＋８
＝２ｘ2－10ｘ＋12＝０ ←÷２
ｘ2－５ｘ＋６
＝（ｘ－２）（ｘ－３）＝０
ｘ＝２、３
*最初に（ｘ－２）で割らないこと！
ｘ＝２のときｘ－２＝０となり、０で割ってしまうから。
（４）
通学時間の短い順から200番目と201番目の平均をとる。
*中央値の求め方を説明する。偶数個の場合は平均。
（５）
『ｙがｘの関数である』→ｘの値を決めると、ｙの値もただ１つに決まる関係。
ア：高さがわからないと三角形の面積ｙは定まらない。×
イ：１辺の長さはｘ/４ｃｍ。ｙ＝（ｘ/４）2＝ｘ2/16〇
ウ：結果を確実に予測することはできない×
エ：ｙ＝20ｘ－300（ｘ≧15）〇
イ・エ
（６）
素数→約数が１か自分自身しかない数。１は含まない。
２・３・５・７・11・13
（７）
余りは１である。
（説明）
整数ｍ、ｎを用いて、
６で割ると５余る数を６ｍ＋５、３で割ると２余る数を３ｎ＋２とすると、
（６ｍ＋５）＋（３ｎ＋２）
＝３（２ｍ＋ｎ＋２）＋１
２ｍ＋ｎ＋１が整数だから、６で割ると５余る数と３で割ると２余る数の和を
３で割ったときの余りは１になる。
*必ず異なる２種類の文字を使うこと！
６ｍ＋５、３ｍ＋２ではバツ！
ｍ＝１のとき、11と５の組み合わせに固定されてしまう→すべての場合を証明したことにならない。
（８）
∠ＡＢＣの二等分線と辺ＡＣの垂直二等分線の交点Ｐを作図する。
教科書通りの問題ゆえ必答。
大問２（確率）
（１）
表→歩く（12分）
裏→走る（６分）
ただし、２連続で走れない。
〔走・歩・走・歩〕か〔歩・走・歩・走〕のいずれか。
12×２＋６×２
＝36分
（２）
42分かかるということは、歩くが３回、走るが１回。
表を〇、裏を●とする。
●〇〇〇
〇●〇〇→（●●〇〇）
〇〇●〇→（〇●●〇）
〇〇〇●→（〇〇●●）
先に表３枚、裏１枚の４パターンを考える。
条件から●の１個手前の〇も●に変えられる。
計７通り。
全体は２4＝16通りだから、確率は７/16
大問３（方程式）
（１）
昨日の鮭は600個。
30％減→70％
600×70％＝420個
（２）ア
表で情報整理する。
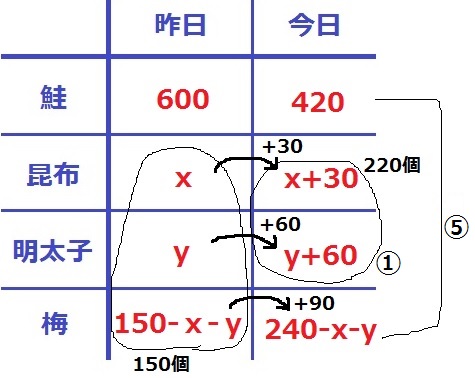
昨日の昆布をｘ、明太子をｙとする。
昨日の昆布＋明太子＋梅＝150個だから、昨日の梅は150－ｘ－ｙ個。
昨日の鮭の５％→600×５％＝30個
10％、15％はその２倍、３倍だから、それぞれ60個、90個。
今日の昆布はｘ＋30個、明太子はｙ＋60個、梅は240－ｘ－ｙ個となる。
１つ目は、今日の昆布と明太子が220個。
（ｘ＋30）＋（ｙ＋60）＝220 …①
２つ目は、今日の鮭＋梅が明太子の５倍。
420＋（240－ｘ－ｙ）＝５（ｙ＋60） …②
イ
先ほどの連立を解く。簡単になおすと、
ｘ＋ｙ＝130 …①’
ｘ＋６ｙ＝360 …②’
これを解くと、ｘ＝84、ｙ＝46
＠余談＠
連立を使わなくても答えは出せてしまう。
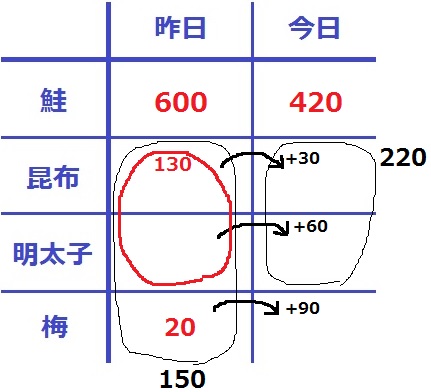
昨日の昆布＋明太子の数は、220－90＝130個
昨日の梅は150－130＝20個
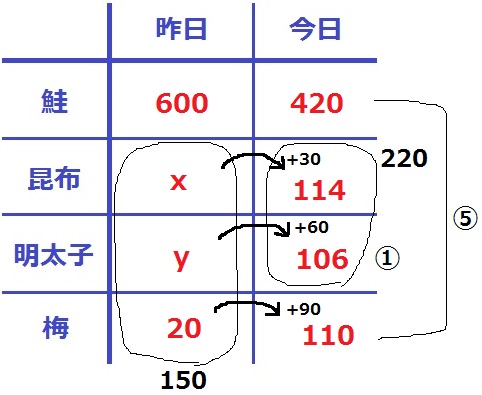
今日の梅は、20＋90＝110個
今日の明太子が、（420＋110）÷５＝106個
今日の昆布が、220－106＝114個
ｘ＝114－30＝84
ｙ＝106－60＝46
はじめはこちらで解いてしまい、どこで連立を組むべきか迷いました。
大問４（数量変化）
（１）ア
Ａ：ｙ＝ａｘにａ＝２、ｘ＝２を代入。ｙ＝２×２＝４
Ｂ：ｘ＝２→０≦ｘ＜３のときだから、ｙ＝２
Ａ…４、Ｂ…２
イ
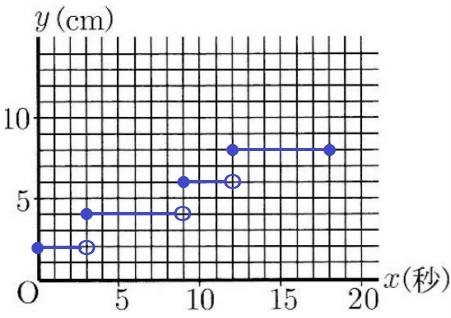
Ｂは３、９、12秒後にパッと瞬間移動する。
不等号で＝がつくと●、つかないと〇。
最後の18秒後は●である。
ウ
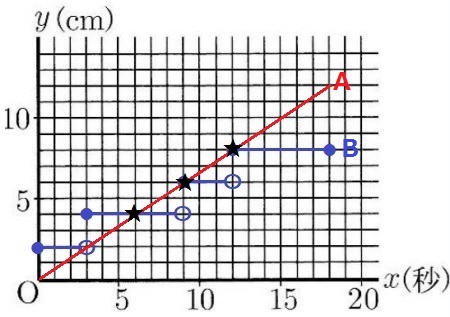
先ほどのグラフにｙ＝２/３ｘをのせる。
傾きが２/３→原点から右に３、上に２移動して格子点を結んでいく。
ｘ＝３は〇なので含まない！
ｘ＝６、９、12
（２）
とりあえず、わかるところだけグラフに描く。
Ｃ；ｙ＝１/16ｘ2の格子点は（４、１）（８、４）（12、９）
Ｄの３≦ｘ＜12が不明で、これを２段階に分けて、
ＣとＤがちょうど２回重なるようにする。
さらに、カッコ内の値を最大にするので、
ｙ＝６のときの左端の●（★）でｙ＝１/16ｘ2が交わればいい。
ｙ＝１/16ｘ2にｙ＝６を代入。
６＝１/16ｘ2
ｘ2＝96
ｘ＞０より、ｘ＝４√６
大問５（平面図形）
（１）
ＡＤ＝ＢＦの証明。
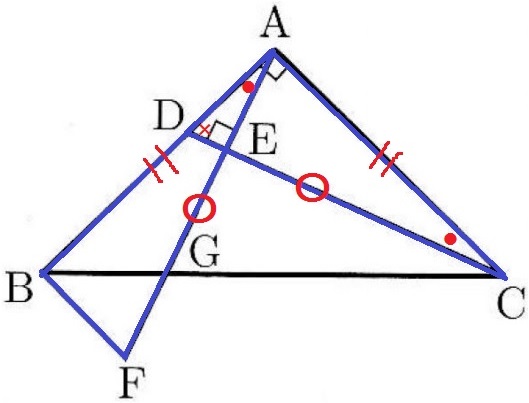
与えられた情報から方針は立てやすい。
ＡＤとＢＦを１辺とする△ＡＣＤと△ＢＡＦの合同を証明すればいい。
仮定より、ＣＤ＝ＡＦ
直角二等辺三角形ＡＢＣの等辺から、ＡＣ＝ＢＡ
△ＡＣＤの内角で、∠ＡＣＤ＝●、∠ＡＤＣ＝×とする。（●＋×＝90）
△ＡＤＥの内角で、∠ＤＡＥ＝180－90－×＝●
∠ＡＣＤ＝∠ＢＡＦ＝●
２辺とあいだの角が等しく、△ＡＣＤ≡△ＢＡＦ
対応する辺でＡＤ＝ＢＦ
（２）ア
ＡＤ＝①、ＤＢ＝②とすると、先ほどの合同よりＡＣ＝③、ＢＦ＝①
△ＡＣＤで三平方→ＤＣ＝〇√10
また、前問の証明で△ＡＣＤと△ＥＡＤの角度が等しかった。
△ＡＣＤ∽△ＥＡＤより、面積比は△ＡＣＤ：△ＥＡＤ＝①2：（〇√10）2＝【１】：【10】
△ＡＥＣの面積比は【９】
合同で△ＢＡＦの面積比も【10】
また、∠ＡＢＦ＝90°を利用して錯角でＡＣ//ＢＦ
ここから△ＣＡＧ∽△ＢＦＧがいえる。
ＡＧ：ＧＦ＝ＡＣ：ＦＢ＝③：①
→△ＢＧＡ：△ＢＦＧの面積比が③：①であり、
△ＢＦＧの面積比は、【10】×①/④＝【５/２】
△ＢＦＧ：△ＡＥＣ
＝【５/２】：【９】
＝５：18
イ
ＡＣ//ℓ//ＢＦより、∠ＡＢＦ＝90°からＢＦが回転体の高さにあたる。
ＢＦ＝√２×①/③＝√２/３ｃｍ
回転体の半径が知りたい。
ℓとＡＢの交点をＨとすると、∠ＢＨＧ＝90°だからＢＨが回転体の半径となる。
前問の△ＣＡＧ∽△ＢＦＧで、ＢＧ：ＧＣ＝《１》：《３》
ℓ//ＡＣより、ＢＨ：ＨＡ＝ＢＧ：ＧＣ＝①：③
ＢＨ＝√２×①/④＝√２/４ｃｍ
回転体をイメージ。
円柱から上下の円錐を引けば、求積すべき立体がでてくる。
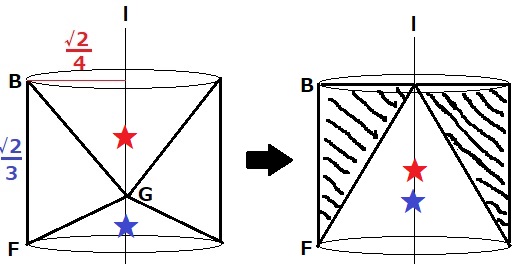
上の円錐★と下の円錐★は底面が等しく、高さの合計が√２/３ｃｍ。
ということは、等積変形のように考えると★★を一体化すれば右のような円錐になる。
円錐は円柱の体積の３分の１⇒求積すべき立体は円柱の体積の３分の２！
√２/４×√２/４π×√２/３×２/３＝√２/36πｃｍ3
大問１
１問あたりの配点が大きいので慎重に。
（４）中央値の求め方がダイレクトに問われた。
（６）説明では別の文字を置くこと！高校数学でも似たような証明問題が出てくる。
大問２
走る区間が２連続しない条件をおさえる。
大問３
（２）ア：実力差がでやすい。立式の前にきちんと情報整理する。
イと合わせて配点が８点もある。
大問４
特殊な動点の問題。ＢとＤは瞬間移動するので、グラフは階段状になる。
（１）イ：ｘ＝18に注意！
ウ：ｘ＝３に注意。
（２）Ｄの２段目と３段目をどう配置するか。
２段目のｙ＝４が通過するのは明白なので、
３段目のｙ＝６の左端●でｙ＝１/16ｘ2が交わるようにすればいい。
大問５
（１）方針は立てやすい。角度の認定が壁。
（２）ア：難易度がグッとあがる。前問の証明がヒント。
直角三角形ＡＣＤの中の直角三角形ＥＡＤが相似。（頻出の相似形）
最も面積が小さい△ＥＡＤを【１】として計算すると、△ＡＥＣの面積比は【９】
△ＢＦＧは別の角度から攻める。
90°を手掛かりにＡＣ//ＢＦ→△ＢＡＧ：△ＢＦＧにつなげたい。
あとは△ＢＡＦ＝△ＡＣＤ＝【10】を１：３で分ける。
イ：直線ℓがＢＦと平行であること。前問の△ＣＡＧ∽△ＢＦＧも使う。
さらに回転体が円柱の３分の２である点を考慮する必要がある。
難問の部類にはいるので、無理そうなら他の見直しに費やすのが賢明。
公立高校入試解説ページに戻る
コメント