平均53.2点(前年比;+6.2点)
問題はこちら→リセマムさん
大問1(小問集合)
(1)
3-5×(-2)
=3+10
=13
(2)
5y×8x3y÷10xy
=4x2y
(3)
√18-4/√2
=3√2-2√2
=√2
(4)
2(5a-b)-3(3a-2b)
=10a-2b-9a+6b
=a+4b
(5)
x+3y=1 …①
y=2x-9 …②
②を①に代入すると、x+3(2x-9)=1
7x=28
x=4
②に代入して、y=2×4-9=-1
x=4、y=-1
(6)
x2-7x-18
=(x+2)(x-9)=0
x=-2、9
(7)
りんご2個…2a円
オレンジ3個…3b円
これらの和が1000円以下だから、
2a+3b≦1000
(8)
【少なくとも1枚が表=全体-すべて裏】
全体は、23=8通り
すべて裏は1通り
少なくとも1枚が表は、8-1=7通り
確率は7/8
(9)
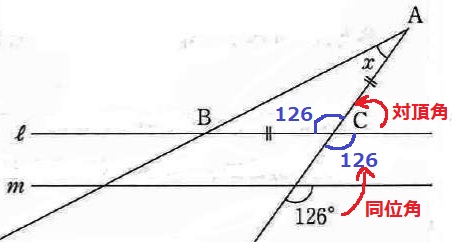
同位角と対頂角で126°を移す。
△ABCは二等辺だから、∠x=(180-126)÷2=27°
大問2(関数)
(1)
アは下に凸のグラフ。a>0でy=x2
傾きの絶対値が大きいほど、グラフの開きは小さくなる。
(y=-100x2は変化の割合がとても大きく、グラフの形はとがる)
イ:y=-2x2、ウ:y=-x2、エ:y=-1/2x2
エ
(2)
y=x2にx座標を代入。
A(-1、1)→C(3、9)
右に4、上に8だから、傾きは8/4=2
切片はAから右に1、上に2移動して、1+2=3
y=2x+3
(3)

B(2、4)
x=2とACとの交点をDとする。
y=2x+3にx=2を代入→D(2、7)
△ABCは幅4、高さ3だから、面積は4×3÷2=6
大問3(データの活用)
(1)

四分位範囲=第3四分位数(Q3)-第1四分位数(Q1)
*箱の長さである。
85-32=53分
(2)
35人の中央値(第2四分位数;Q2)は、(35+1)÷2=18番目
Q3は上位17個の真ん中で下から27番目(上から9番目)の値。
55分
(3)
ア:箱の長さは1組の方が大きい。×
イ:範囲(レンジ)=最大値-最小値
1組…115-15=100分、2組…図2より105-5=100分で等しい。〇
ウ:図2より2組には55分がいるが、1組は不明。×
エ:Q1は下から9番目の値→9人は32分以下。1組の33分以下は少なくとも9人いる。〇
オ:箱ひげ図に×印などをつけて平均値を表すこともできるが、それがないので1組は不明。×
ちなみに、2組を電卓で計算したら約37.9分でした。
イ・エ
大問4(空間図形)
(1)

三角錐D―AEBで捉えるとわかりやすい。
4×4÷2×4÷3=32/3cm3
(2)
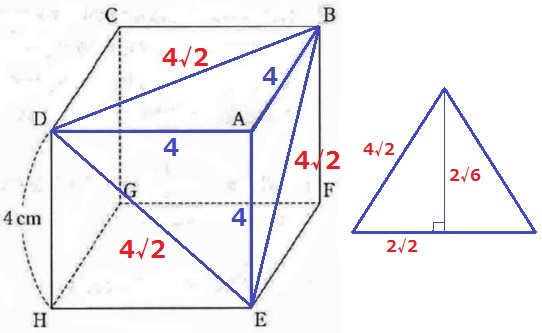
直角二等辺ABDの辺の比1:1:√2より、BD=4√2
△BDEの各辺は合同な正方形の対角線→3辺の長さが等しいから正三角形。
1辺が4√2cmの正三角形の面積を求めればいい。
正三角形を半分に割り、1:2:√3の直角三角形から高さは2√2×√3=2√6cm
4√2×2√6÷2=8√3cm2
@正三角形の面積@
1辺aの正三角形の面積→√3/4a2
√3/4×(4√2)2=8√3cm2
(3)
Aと△BDEの距離→三角錐A―BDE(底面が△BDE)の高さを求める。
32/3×3÷8√3=4√3/3cm
大問5(規則)
(1)
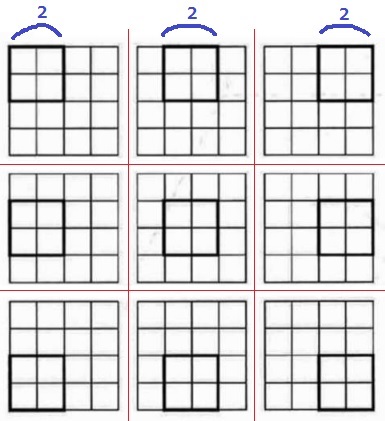
1辺4cmの図が3×3=9個だから
1辺5cmの図は4×4=16個と予想できる。
規則で考えると、1辺4cmから2cmを取り出すと3個あるから、
これを式で表すと、4-2+1=3個→3×3=9個
1辺5cmから2cmを取り出すと、5-2+1=4個
4×4=16個
(2)
1×1cm→5×5=25個
2×2cm→4×4=16個
3×3cm→3×3=9個
4×4cm→2×2=4個
1×1cm→1×1=1個
1+4+9+16+25=55個
(3)
先ほどと手順が逆になる。
169→13×13
〇cmから2cmを取り出したら13個。
〇-2+1=13
〇=13-1+2=14cm→14番目
1辺14cmから8cmを取り出すと、14-8+1=7個
7×7=49個
14番目、49個
大問6(数量変化)
(1)
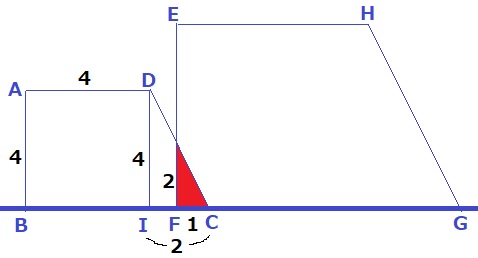
Dに垂線をおろし、足をIとする。
△DICと重なる部分は∽
底辺:高さ=1:2なので、重なる部分の面積y=1×2÷2=1
(2)
グラフの転換点を調べていく。

0≦x≦2は、重なる部分の底辺と高さがともに伸びるから、面積はy=ax2で増加する。
x=2のとき、y=2×4÷2=4

2≦x≦6は、台形の横(上底+下底)だけが伸びるので、面積は一次関数で増加。
x=6のとき、(4+6)×4÷2=20
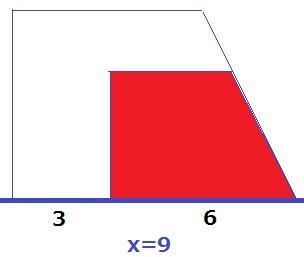
台形の相似比から、FG(大きい台形の下底)=6×3/2=9
6≦x≦9は小さい台形がすべて重なる。y=20を維持。
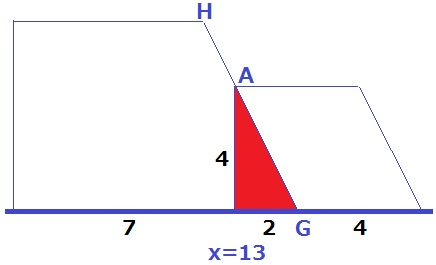
AがHG上にくるのはx=13のとき→xの変域は0≦x≦13となる。
9≦x≦13は台形の横(上底+下底)だけが縮むので、面積は一次関数で減少。
x=13のとき、y=2×4÷2=4
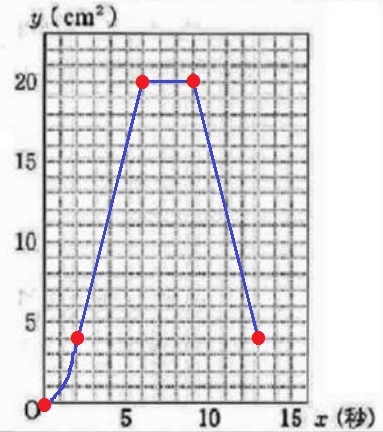
まとめると、xの変域は0≦x≦13
グラフは原点→(2、4)→(6、20)→(9、20)→(13、4)を通過する。
(3)
先ほどのグラフで、y=10となるときのxの値が答え。
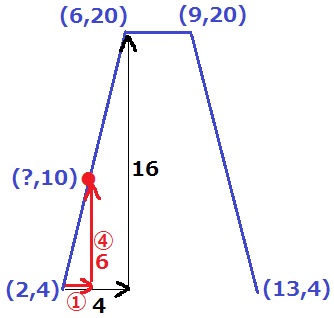
左の直線の傾きを調べる。(2、4)→(6、20)
右に4、上に16だから傾きは4
y座標の差の6が④にあたり、①=6×①/④=3/2
求めるべきx座標は2+3/2=7/2
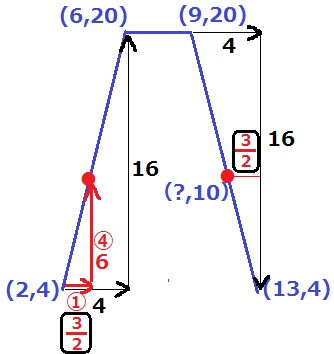
右の直線の傾きは、左に4、下に16で傾きが-4
グラフ全体を見渡すと対称的な跳び箱の形。
求めるべきx座標は13から左に3/2で、13-3/2=23/2
x=7/2、23/2
大問7(平面図形)
(1)
△CAD∽△FABの証明。
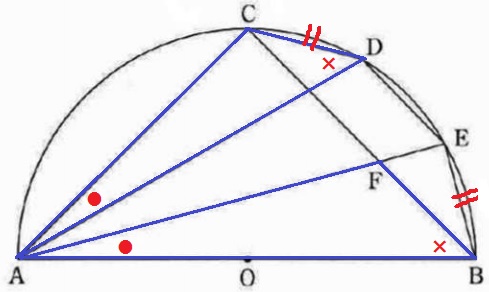
弧CD=弧EBの円周角(●)と、弧ACの円周角(×)から2角相等で∽
(2)①
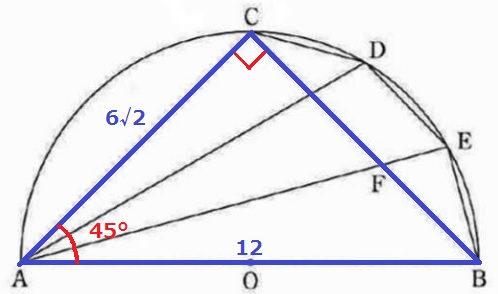
半円の弧に対する円周角で、∠ACB=90°
△ABCの内角は45°ー45°ー90°⇒直角二等辺三角形
辺の比は1:1:√2だから、AC=12×1/√2=6√2cm
CFを1辺とする三角形は△AFC。
相似から攻めようとすると、辺の情報が不足していて使いにくい。
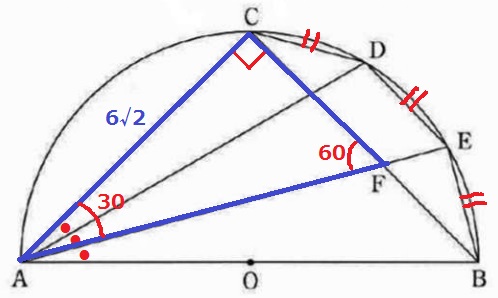
3つの弧の長さが等しい→3つの円周角が等しい(●)
∠CAF=45×2/3=30°
△AFCの内角は30°ー60°ー90°の直角三角形。
辺の比は1:2:√3なので、CF=6√2×1/√3=2√6cm
②
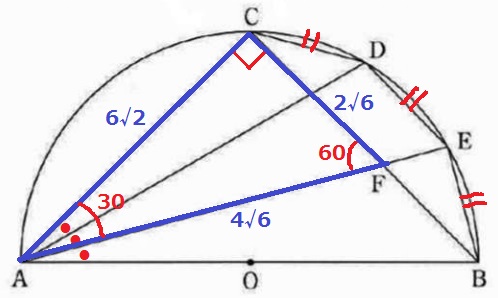
△AFCの辺の比(1:2:√3)より、AF=2√6×2=4√6cm
(1)で△CAD∽△FABは証明済み。
相似比は、AC:AF=6√2:4√6 ←÷2√2
=3:2√3
面積比は相似比の2乗。
△CAD:△FAB
=32:(2√3)2
=3:4
△FABの面積がわかれば、△CADが求まる。
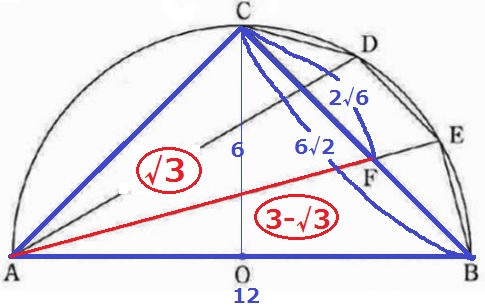
直角二等辺ABCの面積は、12×6÷2=36cm2
△ABC:△AFC=CB:CF
=6√2:2√6
=③:〇√3
△ABCの面積…③
△AFCの面積…〇√3
△FABの面積…〇(3-√3)
△FAB=36×(3-√3)/3=36-12√3cm2
△CAD:△FABの面積比から△CADの面積は、
(36-12√3)×3/4=27-9√3cm2
●講評●
大問1
(5)連立は加減法だけでなく、代入法でも解けるようにしておこう。
(8)少なくともが出たら余事象。
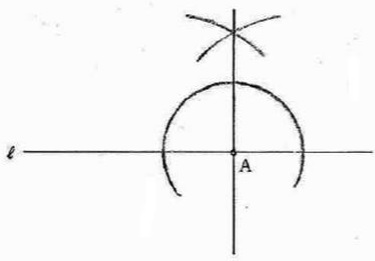
(10)教科書通りの作図。
大問2
(3)どこを高さにするか。
大問3
(2)四分位数は全体を4等分する。中央値をはさんだ方がやりやすいと思う。
(3)2組は個別の数値が開示されている。
大問4
オーソドックスな内容であった。
(3)三角錐の高さは対角線AG上にはない。前問の解答を利用する。
大問5
ここも点が取りやすい。
4と2からどうすれば3が作れるか。4-2+1=3
大問6
(2)細かい長さの認定を要し、少々時間がかかる。忍耐が必要。
(3)グラフの式を求めてy=10を代入してもいい。
解説では図形の対称性を利用して、左側の情報を右側に用いた。
大問7
(2)①相似にハマるとまずい。∠CAF=30°がポイント。
②前問の相似を使うと察する。
ACと対応するAFは△AFCの辺の比から求められる。
面積をいち早く出せるのは直角二等辺ABC。
ここからどうやって△FABの面積につなげるか。



コメント