平均41.2点（前年比；－4.5点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１） 89.3％
３×（－４）＋７
＝－12＋７
＝－５
（２） 83.2％
１/５ａ－３/２ａ
＝－13/10ａ
（３） 64.1％
（－３ｘ）2÷６/５ｘｙ×４ｙ3
＝９ｘ2÷６/５ｘｙ×４ｙ3
＝30ｘｙ2
（４） 75.5％
４ｘ＋３ｙ＝－５ …①
５ｘ＋２ｙ＝６ …②
②×３－①×２をすると、７ｘ＝28
ｘ＝４
②に代入、20＋２ｙ＝６
ｙ＝－７
ｘ＝４、ｙ＝－７
（５） 55.3％
√８（４－√２）
＝２√２（４－√２）
＝８√２－４
（６） 55.2％
（ｘ＋１）2－ｘ（ｘ－２）
＝ｘ2＋２ｘ＋１－ｘ2＋２ｘ
＝４ｘ＋１ ←ここで代入
＝４×２/３＋１
＝11/３
（７） 42.3％
球の体積Ｖ＝４/３πｒ3
４/３π×３3÷２
＝18π
（８） 42.4％
ある得点を仮の平均とする。
（＋７－13＋５－９＋20）÷５＝＋２
（仮の平均）＋２＝平均67点
仮の平均は、67－２＝65点
（９） 57.8％
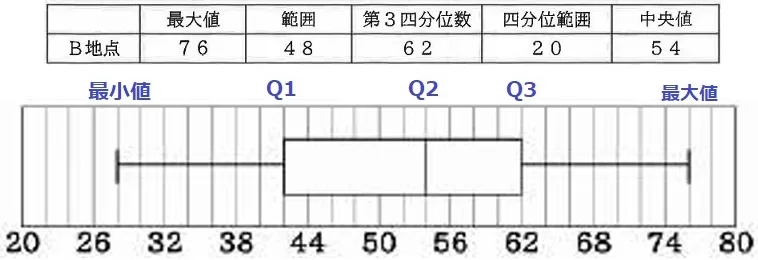
最大値と第３四分位数（Q3）、中央値（Q2）は判明している。
【範囲＝最大値－最小値】
最小値＝76－48＝28
【四分位範囲＝Q3－Q1】
第１四分位数（Q1)＝62－20＝42
大問２（図形・確率）
（１） 29.3％！
正多面体の条件は、
[１]すべての面が合同な正多角形
[２]どの頂点に集まる面の数も同じ
正多面体でない＝いずれかの条件が満たない。
いずれも合同な正三角形なので、[１]は満たす。
頂点に集まる面の数を調べると、Ａ・Ｅは３面だが、Ｂ・Ｃ・Ｄは４面で異なる。
[２]の条件が満たされないから多面体ではない。
＠余談＠
正多面体は５種類しかない。
１つの頂点に集まる面をこれ以上増やすと、360°以上になってしまう。
（２） 1.8％!!
平面Ｐ⊥直線ℓの理由を説明する。
問題文の言い回しから、『Ｏを通る”何か”が直線ℓと垂直である』
→Ｏを通る平面Ｐ上の直線に見当をつける。
留意点は、１本の直線だと面をクルクル回せてしまうので平面Ｐが決定できない！
Ｏで交わる平面Ｐ上の２本以上の直線でなければならない。
解答例：（Ｏを通る）平面Ｐ上の２直線
＠平面の決定条件＠
①同一直線上にない３点を含む平面。
②一直線と、その直線上にない１点を含む平面。
③交わる２直線を含む平面。
④平行な２直線を含む平面。
（３） 33.3％
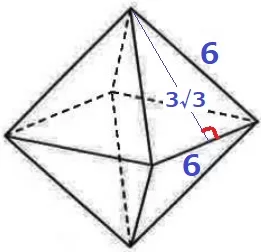
１辺６の正三角形の面積を８倍すればいい。
６×３√３÷２×８＝72√３
（４） 17.6％！
□＝１～４の整数で、□＋□＋□≧10となる組み合わせを調べる。
最も大きい和から考えて、手前の組み合わせの要素を－１していく。
●和が12：（４、４、４）の１通り。
●和が11：４→３に変えて（４、４、３）の３通り。
●和が10：３→２で（４、４、２）、４→３で（４、３、３）が３通りずつ。
計10通り。全体は４3＝64通りだから、確率は10/64＝５/32
５/32＜１/６だから、２つの正六面体を投げる場合の方が確率は高い。
５/32、イ
＠余談＠
●和が９の組み合わせ
（４、４、２）を４→３で（４、３、２）、２→１で（４、４、１）
（４、３、３）を４→３で（３、３、３）
大問３（数量変化）
（１） 28.1％！
立式はしやすい。
時間で一次方程式を立てればいいが、計算がやや大変。。
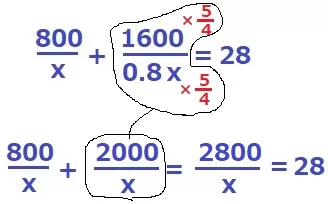
1600/0.8ｘの分母分子を５/４倍すると分母がｘで共通する。
800/ｘ＋2000/ｘ＝2800/ｘ＝28
ｘ＝100
（２）① 34.6％
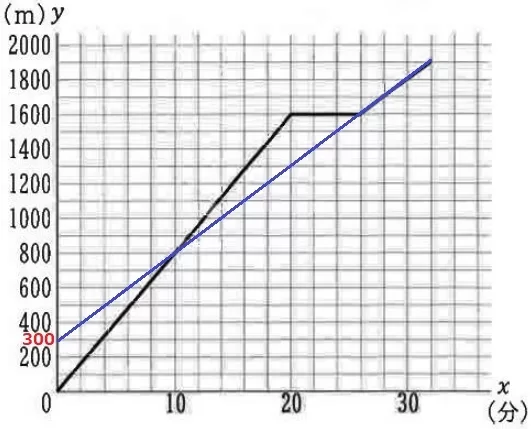
26≦ｘ≦32を延長すると、切片ｂは300。
ｂ＝300
② 2.7％!!
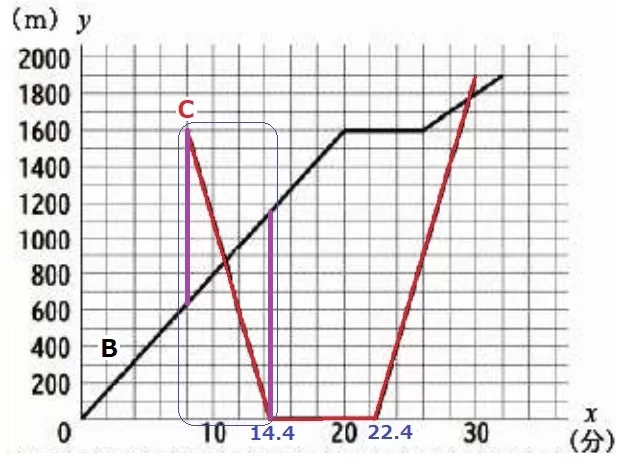
Ｃは８分後に公園を発ち、30分後に図書館に着く。
家での滞在時間が不明なので、スタートとゴールからの移動時間を求める。
公園～家までの時間…1600ｍ÷分速250ｍ＝6.4分
Ｃが家に到着するのは、８＋6.4＝14.4分後
格子点を通らないので目分量で描く。
家～図書館の時間…前より300ｍ長くなるので、300÷250＝1.2分かかる。
Ｃが家を出発するのは、30－（6.4＋1.2）＝22.4分
赤線がＣのグラフ。
＠＠
８≦ｘ≦14.4で、ＢとＣが最も離れる時間を求める。
８分後か14.4分後の２択だが、Ｂの正確な位置を出さなくても目盛りの数で14.4分後とわかる。
大問４（平面図形）
（１） 25.5％！
円外の点を通る接線を作図する。
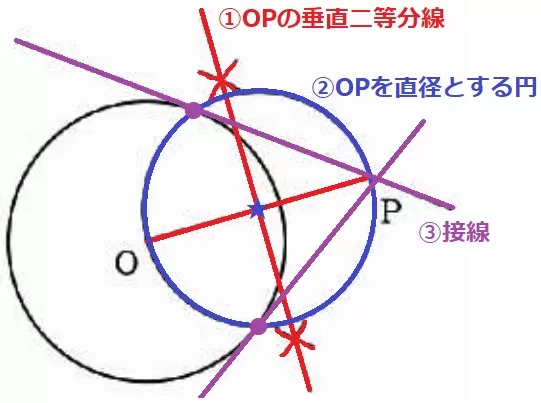
①ＯＰの垂直二等分線
②ＯＰの中点★に針を合わせ、ＯＰを直径とする円を描く。
③上の円と円Ｏの交点とＰを結ぶ。
接線は２本あるので、いずれか１本を作図する。
＠理由＠
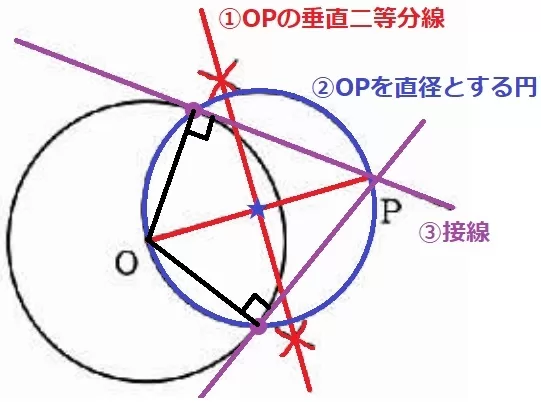
半円の弧に対する円周角は90°だから、円Ｏの半径と接線が直交する。
（２） 10.4％！
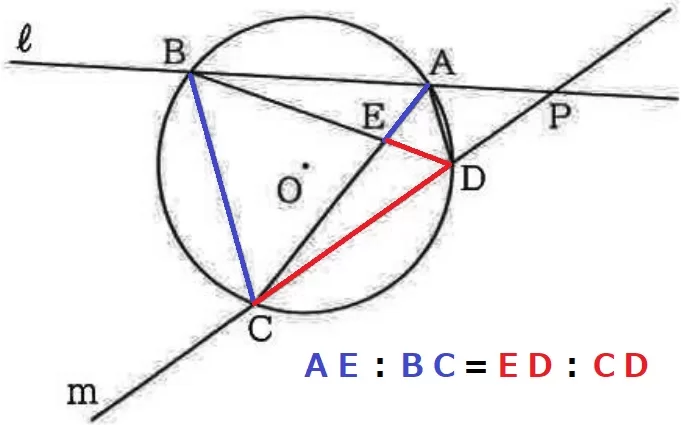
ＡＥ：ＢＣ＝ＥＤ：ＣＤ
→ＡＥとＢＣ、ＥＤとＣＤが対応する辺となる→△ＡＤＥ∽△ＢＤＣを証明すればいい。
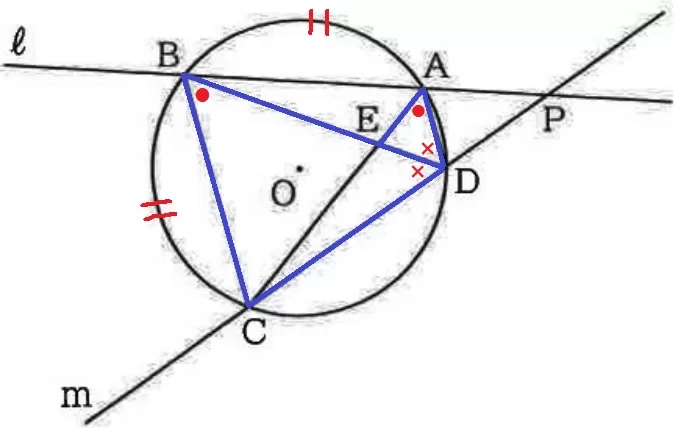
等しい弧に対する円周角は等しい。
弧ＡB＝弧ＡＣより、∠ＡＤＢ＝∠ＢＤＣ（×）
弧ＣＤに対する円周角より、∠ＣＡＤ＝∠ＣＢＤ（●）
２角相等で△ＡＤＥ∽△ＢＤＣ
対応する辺の比から、ＡＥ：ＢＣ＝ＥＤ：ＣＤ
（３） 8.9％!!
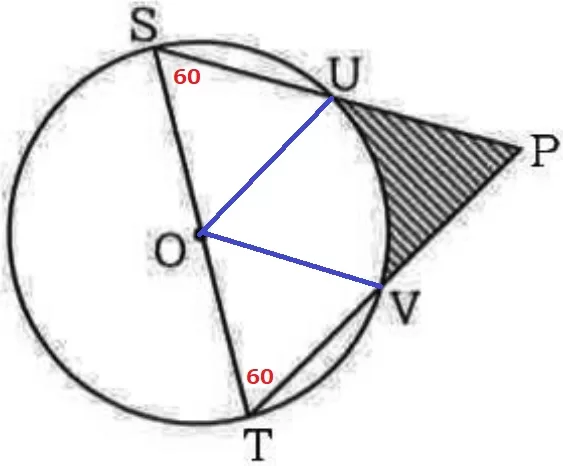
斜線部分が厄介な形をしているので、求めやすい図形から白い部分をひく。
弧をＵＶとする扇形は必要なので、ＯＵとＯＶを結ぶ。
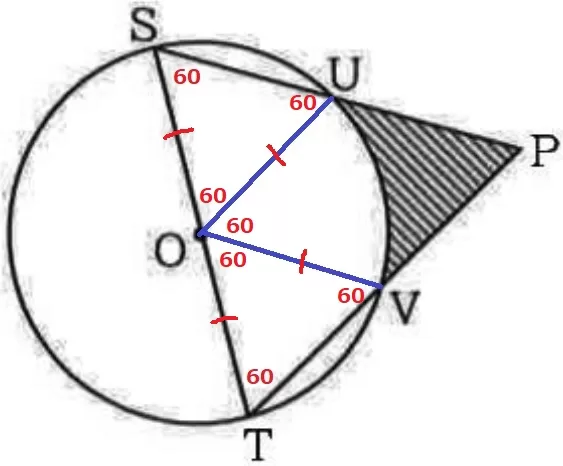
半径よりＯＳ＝ＯＵ→△ＯＳＵは底角60°の二等辺→残りの∠ＳＯＵ＝60°で正三角形。
同様に、△ＯＶＴも正三角形である。
∠ＵＯＶ＝180－60×２＝60°
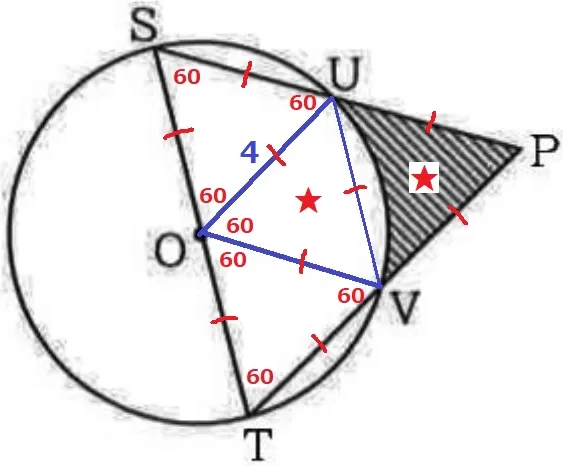
ＵＶをひくと、△ＯＵＶと△ＰＵＶも合同な正三角形。
求積すべき図形は、１辺４ｃｍの正三角形２つから半径４ｃｍ中心角60°の扇形を引けばいい。
正三角形の高さは４×√３/２＝２√３ｃｍ
４×２√３÷２×２－４×４×π×１/６＝８√３－８/３πｃｍ2
50点未満が60％を超えている。
大問１
配点38点。ここで稼いでおきたい。
（８）仮の平均との差を均すと、仮の平均と実際の平均との差が出る。
大問２
（１）専門的な知識はいらない。
与えられた条件に照らして、どの条件が合わないかを述べればいい。
（２）中１の範囲だが、記入式のせいか正答率が著しく低い。
「Ｏを通る」ときたら直線。どんな直線か→『平面Ｐ上』と『２本』が加わる。
頭の中で図形を描いて、クルクル回せるかどうかイメージしよう。
（３）ここは難しくない！
（４）調べ上げのコツとして覚えておこう。
最大の組み合わせから１減らすか、最小の組み合わせから１増やしていく。
大問３
（１）のっけからつまづきやすい。先に0.8ｘを始末しておく。
（２）①（26、1600）→（32、1900）で傾きａと切片ｂを調べてもいいが、
定規で線をひくだけで解けてしまう。間違えるのはもったいない。
②割り算で移動時間を求めるだけで解けるはずだが、正答率がかなり低い。。
グラフを正確に描ければ、後半は計算が不要。
大問４
（１）円周上の点ではなく、円外の点からも接線をひけるようにしたい。
（２）∽→比例式の流れ。∽は見つけやすかったと思うのだが。
（３）ラス問にしては方針は立てやすい。中心角が60°とわかればたどり着ける。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント