問題ＰＤＦ
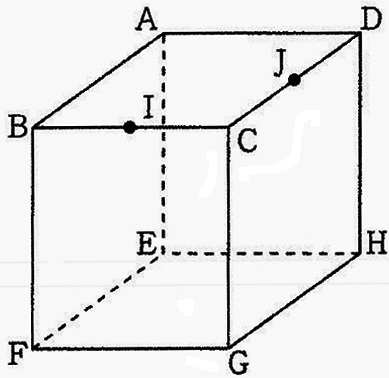
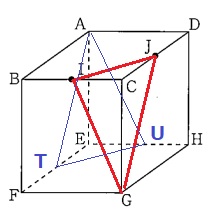
図のような、１辺の長さが６ｃｍの立方体ＡＢＣＤ－ＥＦＧＨがあります。
辺ＢＣ、ＣＤの真ん中の点をそれぞれＩ、Ｊとし、
この立方体を点Ｉ、Ｊ、Ｇを通る平面で切って２つの立体にわけるとき、次の問いに答えなさい。
（１）
切り口の辺は下の展開図のどこにできますか。線をかきこみなさい。
（２）
切ってできた２つの立体のうち、点Ａを含むほうの立体を考えます。
切り口の平面を底面として、１秒あたり９ｃｍ3の水を注ぎます。
水面が次の（ア）～（ウ）の点に達するのは、水を注ぎ始めてから、それぞれ何秒後ですか。
（ア）Ｂ （イ）Ｆ （ウ）Ａ
＠解説＠
（１）
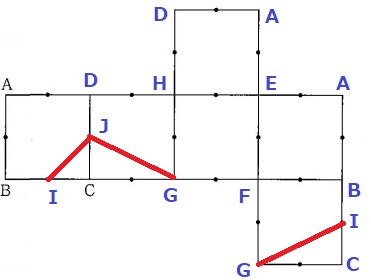
展開図問題。
頂点と点Ｉ・Ｊを書いて結ぶ。
（２）ア
△ＩＧＪを底面とした図形を捉えたいが、これを下にもってきた図形を描くのが難しい…。
ポイントは水面は△ＩＧＪと平行であること！
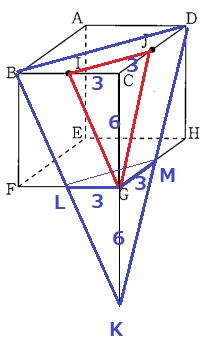
ＩＪ//ＢＤ⇒Ｄが水に触れる。
ＩＧ//ＢＫ、ＪＧ//ＤＫ
平行線を頼りに、ＬとＭは辺の中点にくる。
三角錐Ｋ－ＢＣＤ…６×６÷２×12÷３＝72ｃｍ3
三角錐Ｋ－ＬＧＭ…先の三角錐の８分の１→72÷８＝９ｃｍ3
Ｇ－ＩＣＪもこれと同じ体積。
（72－９－９）÷９＝６秒後
イ
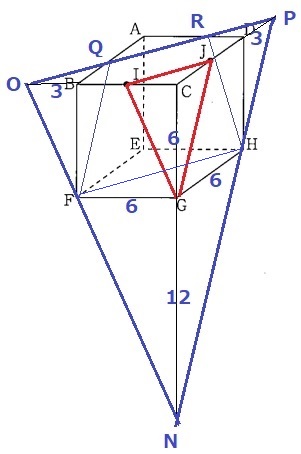
Ｈが水面に触れる。
ＩＪ//ＯＰ、ＩＧ//ＯＮ、ＪＧ//ＰＮ
△ＩＧＣと△ＯＦＢは、直角と同位角で一辺両端角が等しく合同。
ＯＢ＝ＩＣ＝３ｃｍ
ＯＢ：ＢＦ＝１：２から、ＣＮ＝18ｃｍとわかる。
右側の側面も同様。
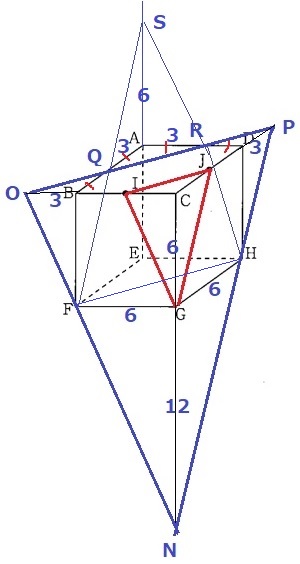
体積は立方体から前と裏をひいた方がいいかも。。
ＱとＲは辺の中点。
延長線をひいて、三角錐Ｓ－ＥＦＨの７/８倍。
ＡＱＲ－ＥＦＨ（裏）…６×６÷２×12÷３×７/８＝63ｃｍ3
立方体から、これとＧ－ＩＣＪをひく。
（６×６×６－63－９）÷９＝16秒後
ウ
Ｇ－ＩＣＴと合同の三角錐Ａ－ＥＴＵが反対側にできる。
（６×６×６－９×２）÷９＝22秒後
難関中（算数科）解説ページに戻る
コメント