2021年度　熊本県公立高校入試・選択問題Ｂ過去問【数学】解説

平均点22.9点（前年比；＋0.7点）
問題はコチラ→ＰＤＦファイル
出題範囲の削減は円周角と中心角の関係、三平方の定理、標本調査。

大問１（計算）

（１）
１/３＋２/７
＝13/21

（２）
８＋７×（－４）
＝８－28
＝－20

（３）
３（ｘ＋ｙ）－２（ｘ－６ｙ）
＝３ｘ＋３ｙ－２ｘ＋12ｙ
＝ｘ＋15ｙ

（４）
（－６ａ）²×２ａｂ²÷（－９ａ²ｂ）
＝36ａ²×２ａｂ²÷（－９ａ²ｂ）
＝－８ａｂ

（５）
（２ｘ＋１）²＋（５ｘ＋１）（ｘ－１）
＝４ｘ²＋４ｘ＋１＋５ｘ²－４ｘ－１
＝９ｘ²

（６）

２√２

大問２（小問集合）

（１）
２ｘ＋７＝１－ｘ
３ｘ＝－６
ｘ＝－２

（２）
（ｘ＋３）（ｘ－３）＝ｘ
ｘ²－９＝ｘ
ｘ²－ｘ－９＝０
解の公式を適用して、
ｘ＝（１±√37）/２

（３）
ｘ＝１のとき、ｙ＝ａ
ｘ＝４のとき、ｙ＝16ａ
変化の割合＝（ｙの増加量）÷（ｘの増加量）
＝（16ａ－ａ）÷（４－１）＝５ａ＝４
ａ＝４/５

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）。
ａ（１＋４）＝４
５ａ＝４
ａ＝４/５

（４）
５個から順番をつけて２個取り出す。₅Ｐ₂＝５×４＝20通り
３ｂ/２ａが整数となる組み合わせを地道に調べる。
ａ＝１のとき、ｂ＝２、４
ａ＝２のとき、ｂ＝４
ａ＝３のとき、ｂ＝２、４
ａ＝４、５のとき、ｂは無い。
以上、５通り。
確率は５/20＝１/４

（５）

①∠ＢＡＰ＝∠ＣＡＰより、Ｐは∠ＢＡＣの二等分線上にある。
②∠ＰＢＡ＝60°から、正三角形を想起。
ＡとＢからＡＢの長さをとって交点をＤとすると、△ＡＢＤは正三角形。
∠ＡＢＤ＝∠ＡＢＰ＝60°となる。
①と②の交点がＰ。

（６）①

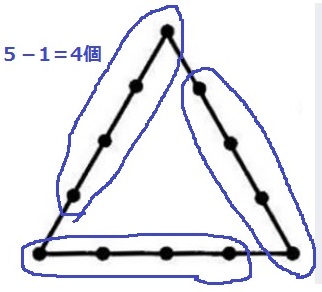
魔方陣の考え。
正三角形の辺上に５個の場合、（５－１）×３＝12個

正ａ角形の辺上にｂ個の場合、１辺にｂ個並ぶからｂ－１個がａ個分できる。
ａ（ｂ－１）
＝ａｂ－ａ個

②
考え方は前問と同様。
正ｎ角形の辺上にｎ個並ぶ→ｎ（ｎ－１）＝ｎ²－ｎ個
正ｎ＋２角形の辺上にｎ＋１個並ぶ→ｎ（ｎ＋２）＝ｎ²＋２ｎ個
ｎ²－ｎ＋24＝ｎ²＋２ｎ
３ｎ＝24
ｎ＝８

（７）①
式で求めるのが王道だが…算数でいきます。

グラフの交点が料金が等しくなるところ。
20ｍ³以降に折れ線がなくなるので、このときの両者の料金を求める。
ヒバリ市…620＋140×10＝2020円
リンドウ市…900＋110×20＝3100円
差は3100－2020＝1080円

ここから両者は１ｍ³あたり170－110＝60円ずつ差が縮まるから、
1080÷60＝18ｍ³
つまり、20＋18＝38ｍ³のときの水道料金を求めればいい。
900＋110×38＝5080円

②

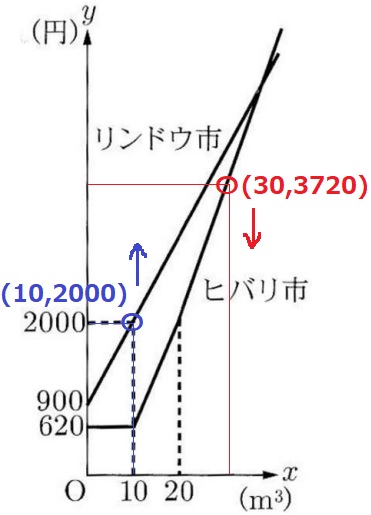
10ｍ³のとき、リンドウ市の2000円より高くする。
30ｍ³のとき、ヒバリ市の水道料金は620＋140×10＋170×10＝3720円でこれより安くする。

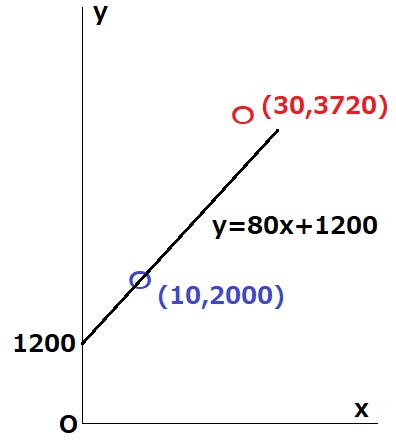
下限から計算してみる。
『１ｍ³につき80円』→傾き80
（10、2000）を通り、傾きが80の式を求める。
（10、2000）から左に10移動すると、下に10×８＝800下がるから、
切片は2000－800＝1200円
直線の式はｙ＝80ｘ＋1200
切片が基本料金ａ。
直線は（10、2000）より上を通過するので、基本料金ａは1200円より高い。（1200は含まない）

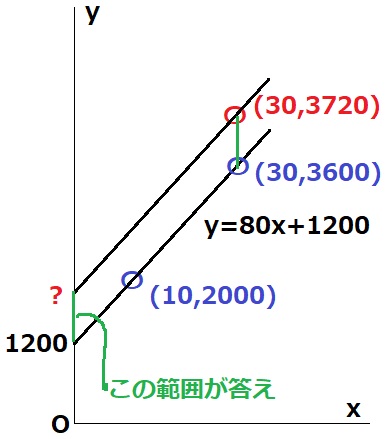
上限はどうか。
傾き80は変化しないので、ｙ＝80ｘ＋1200をどの程度上に平行移動できるか。

ｙ＝80ｘ＋1200にｘ＝30を代入して、
ｙ＝80×30＋1200＝3600
3720－3600＝120だから、ｙ＝80ｘ＋1200をｙ軸方向に＋120すれば、
（30、3720）を通過する傾き80の式が求まる。
ｙ＝80ｘ＋1320
（30、3600）より下を通過するので、基本料金ａは1320円より安い。
したがって、1200＜ａ＜1320

大問３（データの活用）

（１）
ア：範囲（レンジ）は［最大値－最小値］の値。
　度数分布表では最大値・最小値がわからないが、階級値で計算すると45－３＝42分×
　階級の幅が６分。
イ：最頻値（モード）は最もあらわれている値。12～18分の階級値15分。〇
ウ：34人の中央値は17番目と18番目の平均で、いずれも18～24分の階級だから21分。×
エ：８÷34を計算。分母が分子の４倍を超えるから、値は１/４（0.25）より小さい。×
オ：30分以上は３＋２＋１＝６人。６/34で分母は分子の５倍を超えるから１/５（20％）以下。〇
イ・オ

（２）
図１と比較して図２で増えた部分をみると、
０～６分が１人、６～12分が４人、12～18人が３人増えている。
おのおのの階級値で計算。
（３×１＋９×４＋15×３）÷８
＝84÷８＝10.5分＝10分30秒

（３）イ、図２より通学時間が18分未満の生徒が22人いるから。
*平均値と中央値の違いは頻出である。
度数分布表が左に寄っているので、平均より通学時間が短くても順番は半分を超えた。

大問４（空間図形）

（１）

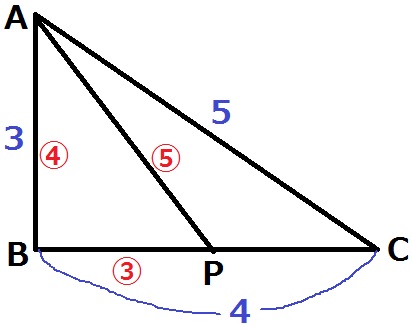
△ＡＢＰ∽△ＣＢＡより、△ＡＢＰの辺の比も３：４：５。
ＢＰ＝３×③/④＝９/４ｃｍ

（２）
底面が△ＡＢＰ、高さＢＥの三角錐だから、
９/４×３÷２×４÷３＝９/２ｃｍ³

（３）

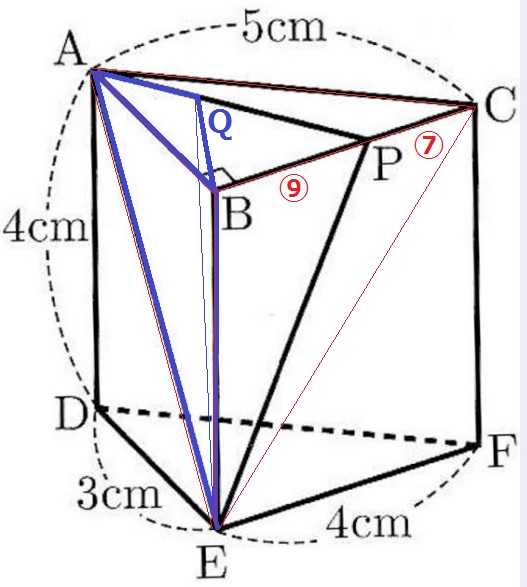
三角柱ＡＢＣ－ＤＥＦの体積を１とする。これを削っていき、三角錘Ｅ－ＡＢＱにする。
【三角柱ＡＢＣ－ＤＥＦ⇒三角錘Ｅ－ＡＢＣ⇒三角錘Ｅ－ＡＢＰ⇒三角錘Ｅ－ＡＢＱ】
（１）よりＢＰ＝９/４ｃｍだったので、ＰＣ＝４－９/４＝７/４ｃｍ
ＢＰ：ＰＣ＝９/４：７/４＝⑨：⑦

１×１/３×⑨/⑯×ＡＱ/ＡＰ＝１/20
３/16×ＡＱ/ＡＰ＝１/20
ＡＱ/ＡＰ＝１/20÷３/16＝４/15
ＡＱ＝４とするとＡＰ＝15だから、ＱＰ＝15－４＝11
ＡＱ：ＱＰ＝４：11

大問５（関数）

（１）
Ａはｙ＝－ｘ＋１上の点。
これにｙ＝３を代入して、３＝－ｘ＋１
ｘ＝－２
Ａ（－２、３）
ｙ＝ａｘ²に代入。
３＝４ａ
ａ＝３/４

（２）
ｙ＝３/４ｘ²にｘ＝４を代入して、Ｃ（４、12）
Ａ（－２、３）⇒Ｃ（４、12）右に６、上に９移動するから、傾きは９/６＝３/２
Ａから右に２、上に３移動して、切片は３＋３＝６
ｙ＝３/２ｘ＋６

（３）①

Ｐ・Ｑ・Ｒの位置に注意すること！
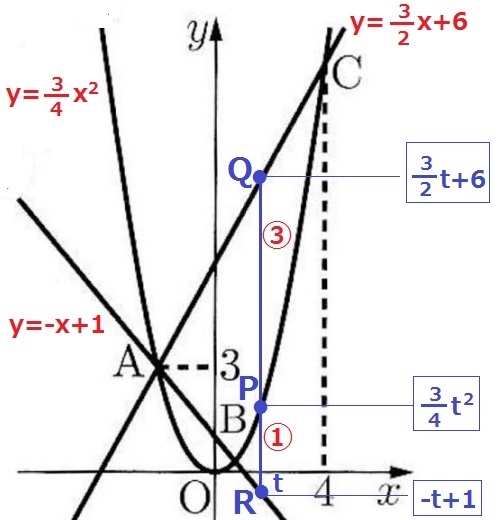
Ｐのｘ座標をｔとする。
ｙ座標はＰが３/４ｔ²、Ｑが３/２ｔ＋６、Ｒが－ｔ＋１。
ＰＱ：ＰＲ
＝（３/２ｔ＋６）－３/４ｔ²：３/４ｔ²－（－ｔ＋１）＝③：①
内項と外項の積で整理すると、
－３/４ｔ²＋３/２ｔ＋６＝９/４ｔ²＋３ｔ－３　←すべてを４倍
－３ｔ²＋６ｔ＋24＝９ｔ²＋12ｔ－12
12ｔ²＋６ｔ－36＝０　←÷６
２ｔ²＋ｔ－６＝０
解の公式を適用。
ｔ＝（－１±７）/４＝－２、３/２

Ｐはｙ＝３/４ｘ²においてＢとＣの間にある点。
Ｂのｘ座標は、－２＋８/３＝２/３
２/３≦ｔ≦４より、ｔ＝３/２
Ｐのｘ座標は３/２。

②

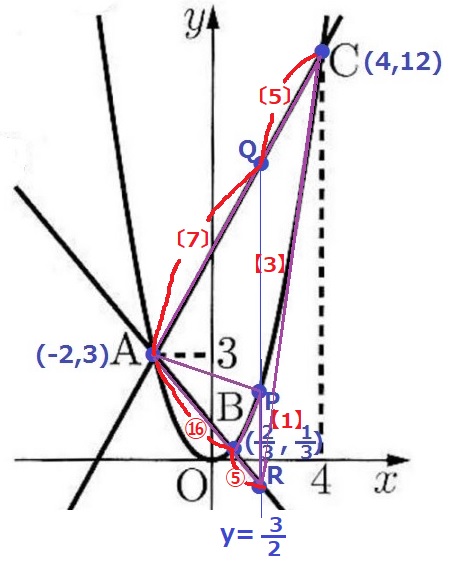
面積比の算出に必要な長さの比をｘ座標の差から計算する。
ＡＢ：ＢＲ＝２/３－（－２）：３/２－２/３
＝８/３：５/６＝⑯：⑤
仮定からＱＰ：ＰＲ＝【３】：【１】
ＡＱ：ＱＣ＝３/２－（－２）：４－３/２
＝７/２：５/２＝〔７〕：〔５〕

△ＡＢＰの面積比を16とする。
【△ＡＢＰ⇒△ＡＲＰ⇒△ＡＲＱ⇒△ＡＲＣ】
△ＡＲＰ…16×㉑/⑯＝21
△ＡＲＱ…21×【４】/【１】＝84
△ＡＲＣ…84×〔12〕/〔７〕＝144

△ＡＲＣ：△ＡＢＰ＝144：16＝９：１
△ＡＲＣは△ＡＢＰの９倍。

大問６（平面図形）

（１）
△ＢＣＦ∽△ＣＤＨの証明。

直角二等辺三角形ＡＢＣより、∠ＦＢＣ＝45°
直角二等辺三角形ＡＣＤより、∠ＨＣＤ＝45°
∠ＦＢＣ＝∠ＨＣＤ

同様に、∠ＡＣＢ＝∠ＡＤＣ＝90°
仮定から∠ＡＣＦ＝∠ＡＤＥ（●）だから、
∠ＦＣＢ＝∠ＨＤＣ＝90－●
２角が等しく∽。

（２）

ＤＨとＨＧを１辺とする相似図形を探す。
△ＡＤＨと△ＧＣＨが２角相等で∽だが、対応する辺ではない…。
とりあえず、２つの三角形で長さがわかる辺を求めてみる。

直角二等辺三角形ＡＣＤより、１：１：√２でＤＣ＝６ｃｍ
（*除外された三平方を使いたくないのであれば、直角二等辺ＡＢＣをうえのように二等分し、
ＡＢを底辺とすると高さＡＤは６ｃｍとなる）

前問の△ＢＣＦ∽△ＣＤＨを活用する。
ＤＨ＝３√５×６/６√２＝３√10/２ｃｍ

△ＡＨＥ∽△ＣＤＨ（対頂角と45°）より、ＡＨ：ＨＣ＝ＡＥ：ＣＤ＝①：③
ＡＣ＝６√２ｃｍだから、これを①：③に分けて、
ＡＨ＝３√２/２ｃｍ、ＨＣ＝９√２/２ｃｍ

最後に△ＡＤＨ∽△ＧＣＨ。
ＧＨ：ＨＣ＝ＡＨ：ＨＤ＝３√２/２：３√10/２＝１：√５
ＨＧ＝９√２/２×１/√５＝９√10/10ｃｍ
したがって、ＤＨ：ＨＧ＝３√10/２：９√10/10＝５：３

＠別解＠

ＤＨ＝３√10/２ｃｍ、ＤＣ＝６ｃｍまでは先ほどと同じ。
さらに角度を調べていく。
△ＡＨＥ∽△ＣＨＤで∠ＨＥＡ＝×（もしくは、ＤＣ//ＡＢの錯角でＯＫ）
対頂角で∠ＧＥＦ＝×
△ＥＦＧと△ＣＦＢで、残りの内角から∠ＥＧＦ＝∠ＣＢＦ＝●
２角が等しく、△ＢＣＦ∽△ＧＤＣ。
ＤＧ＝６√２×６/３√５＝12√10/５ｃｍ

ＤＨ：ＤＧ＝３√10/２：12√10/５＝５：８
ＤＨ：ＨＧ＝５：３