2019年度　富山県公立高校過去問【数学】解説

平均61.3点
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
８＋３×（－２）
＝８－６＝２

（２）
９ａ＋１－２（３ａ－２）
＝９ａ＋１－６ａ＋４
＝３ａ＋５

（３）
８ｘ²ｙ×（－６ｘｙ）÷12ｘｙ²
＝－４ｘ²

（４）
９/√３＋√12
＝３√３＋２√３＝５√３

（５）
３ａ＋５ｂ＞500
〔より〕なのでイコールではない。

（６）
ｘ²＋ｘ－６
＝（ｘ＋３）（ｘ－２）＝０
ｘ＝－３、２

（７）
ネジレの位置→延長しても交わらない、かつ平行でない。
辺ＣＦ、辺ＤＦ、辺ＥＦの３本。

（８）
２点から等しい距離にある点⇒垂直二等分線上にある。
ＡＢ・ＢＣ・ＣＡから２本の垂直二等分線を描き、その交点がＰとなる。
（３点Ａ・Ｂ・Ｃが円周上にくる円の中心点の作図と同じ）

（９）

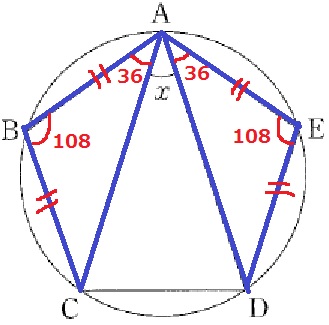
正五角形の内角の１つは108°。
△ＡＢＣと△ＡＥＤはともに二等辺で、
その底角は、（180－108）÷２＝32°
ｘ＝108－36×２＝36°

＠余談＠

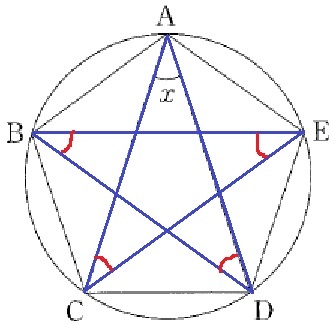
星型の先端の角の和は180°なので、
ｘ＝180÷５＝32

（10）
４個から２個を取り出す→₄Ｃ₂＝６通り
和が５となる組み合わせ→（１と４）（２と３）
２/６＝１/３

大問２（小問集合２）

（１）①
連立方程式を作成する。
ｘ＋ｙ＝365
0.8ｘ＋0.6ｙ＝257

②
上の連立を解く。
ｘ＝190、ｙ＝175
男子は190人、女子は175人。

（２）①
ア：１組は35人。平均は112÷35＝3.2冊○
イ：35人の中央値は18番目の値。少なくとも18～35番目の18人は３冊以上×
ウ：36人いて最頻値が２冊。最小値１、最大値５なので、１冊～５冊までいる。
仮に１冊～５冊まで35人が均等にバラけたとき、各々、35÷５＝７人。
２冊の人数を最も多くするので、２冊の生徒は８人以上でなければならない○

大問３（関数）

（１）
ｘ＝－４のとき、ｙ＝４
ｘ＝－２のとき、ｙ＝１
（１－４）/{－２－（－４）}＝－３/２

もしくは、ｙ＝ａｘ²においてｐ→ｑの変化の割合はａ（ｐ＋ｑ）
１/４×（－４－２）＝－３/２

（２）
Ｃ（２、１）Ｄ（４、４）
右に２、上に３なので、傾きは３/２。
Ｃから左に２、下に３→（０、－２）

（３）
回転させるとプリン型になる。

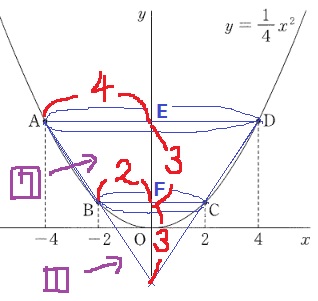
ＡＢとＤＣを延長して円錐をつくる。
体積比は辺の比の３乗。
下の小さな円錐との体積比は、１³：２³－１³＝１：７
４×４×π×６×１/３×７/８＝28π

大問４（規則）

（１）
７行目の一番左は、２×７＝14
左から４番目なので、数字は３つ増える。（一番左の数もカウントするため）
14＋３＝17

（２）
ｎ行目の一番左は２ｎ。
ｎ行目ではｎ個の数が横に並ぶ。
一番右は一番左の数にｎ－１を足す。
２ｎ＋（ｎ－１）＝３ｎ－１

（３）
視点を縦の列にみる。

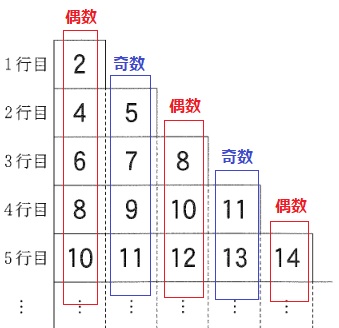
偶数列と奇数列が繰り返される。
31は奇数なので、奇数列に表れるはず。

問題は、列の出発点が31を超えるところはどこか。
列の出発点は行の一番右の数字。
仮に31が一番右の数字であった場合、前問の答えから、
３ｎ－１＝31
ｎ＝10.333…
整数にならないということは、31は一番右にこない。
31に近い数字が10～11行目に来る。
ｎ＝10で試すと、３×10－１＝29
ｎ＝11では、一番右の数は３ずつ増えるため、29＋３＝32
11行目で31を超えるので、10行目までの奇数列の数が答えとなる。
10÷２＝５個

大問５（空間図形）

（１）①
容器の２/３まで水を入れたので、図１の水の高さは６×２/３＝４ｃｍ

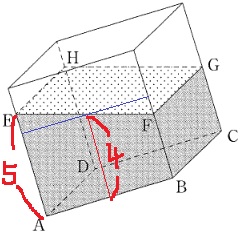
水の体積は変わらない。
正面からみたとき、奥行きはＢＣで同じだから、
高さ４ｃｍの長方形と台形ＡＢＦＥは面積が同じ。
高さ４ｃｍの長方形を作成する。
青い線より上の直角三角形と下の直角三角形は合同で、ＡＥとＢＦの平均は４ｃｍとなる。
ＢＦ＝５－１＝３ｃｍ

②

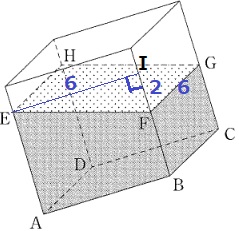
Ｅから垂線をおろし、交点をＩとする。
△ＥＦＩで三平方。
ＥＩ＝√（６²＋２²）＝２√10
長方形ＥＦＧＨ＝２√10×６＝12√10ｃｍ²

（２）
球を沈め、取り出したあとに残る水の体積が知りたい。

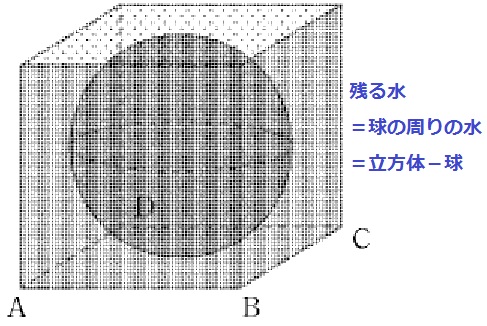
球を沈めた状態から球を取り除くので、球の周りの水が残る。
【残る水＝立方体－球】
残る水の体積は、６³－４/３π×３³
＝216－36πｃｍ³
底面積は36ｃｍ²なので、水面の高さは、
（216－36π）÷36＝６－πｃｍ

大問６（数量変化）

（１）
ＱＲ＝２ｃｍ
ｘ＝４のとき、ＰはＢとＣの中点にくる。
ＱＲを底辺としたとき、高さは７ｃｍ
ｙ＝２×７÷２＝７

（２）
Ｐは５秒後にＣに着く。
ＣＤは斜め線なので、△ＣＤＥから三平方。

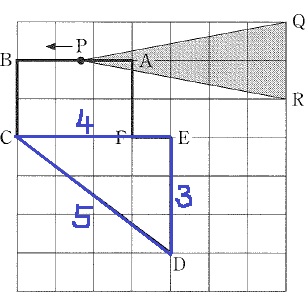
３：４：５の直角三角形がみつかる。
Ｐは10秒後にＤに着く。
５≦ｘ≦10

（３）
ＱＲを底辺としたとき、高さが変わると△ＰＱＲの面積も変わる。
高さが変わらなければ、等積変形で面積も変わらない。

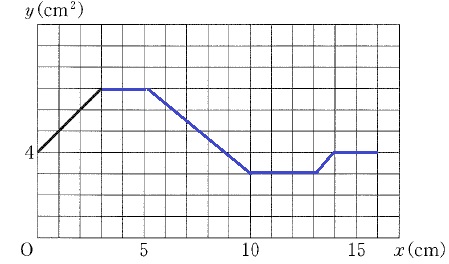
ＰがＢ・Ｃ・Ｄ・Ｅ・Ｆにきたときにグラフが折れる。
16秒後にＡへ戻る。

（４）
先ほどのグラフで、ｙ＝６の横線を描く。

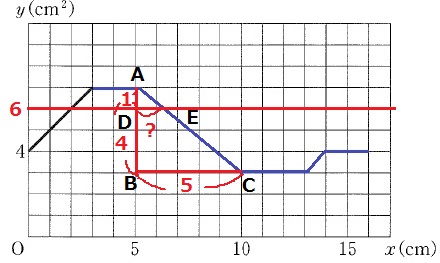
２つの交点が答え。
１つ目は２秒後と決まるが、２つ目が中途半端なところで交わる。
そこで相似を使う。
△ＡＤＥ∽△ＡＢＣ
ＢＣ：ＤＥ＝ＡＢ：ＡＤ＝４：１
ＤＥ＝５×１/４＝５/４
Ｅのｘ座標は、５＋５/４＝25/４
ｘ＝２、25/４

大問７（平面図形）

（１）
△ＡＢＥ≡△ＡＣＤの証明。
難しくはないので正解したい。

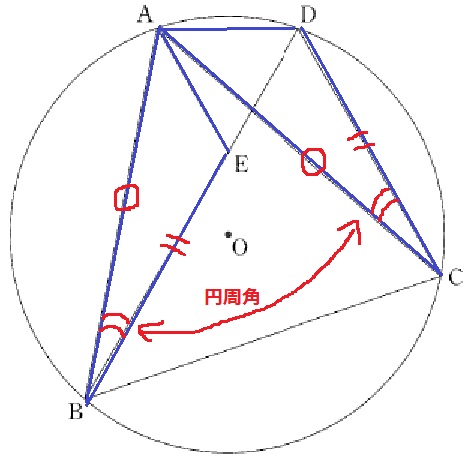
仮定より、ＢＥ＝ＣＤ
正三角形の一辺より、ＡＢ＝ＡＣ
弧ＡＤに対する円周角から、∠ＡＢＥ＝∠ＡＣＤ
２辺とあいだの角が等しいので合同となる。

（２）①
△ＡＤＥが正三角形っぽい・・。
この直感が正しいか検証する。

前問の合同から、ＡＥ＝２ｃｍ、ＢＥ＝４ｃｍ
∠ＢＡＣ（×＋●）は、正三角形の内角の１つで60°。
合同より、∠ＢＡＥ（×）＝∠ＣＡＤ（×）だから、
∠ＥＡＤ＝×＋●＝60°
ＡＤ＝ＡＥより、△ＡＤＥは二等辺。
頂角である∠ＥＡＤ＝60°から、残りの角度もすべて60°となり、
△ＡＤＥは正三角形となる。

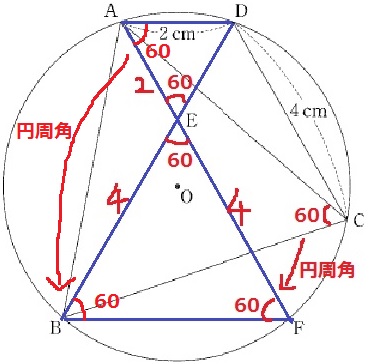
△ＢＦＥも正三角形っぽい・・。
対頂角より、∠ＢＥＦ＝60°
弧ＡＢに対する円周角から、∠ＡＣＢ＝∠ＥＦＢ＝60°
弧ＤＦに対する円周角から、∠ＥＡＤ＝∠ＥＢＦ＝60°となり、△ＢＦＥも正三角形。

つまり、求面すべきところは、１辺が４ｃｍの正三角形となる。
底辺４ｃｍ、高さ２√３ｃｍ
４×２√３÷２＝４√３ｃｍ²

②
ＢＣは正三角形の一辺。
ポイントは外角60°を活用する。

ＡからＢＤに向けて垂線を描き、交点をＨとする。
∠ＡＥＨ＝60°、∠ＥＡＨ＝30°
△ＡＥＨは30°－60°－90°の直角三角形であり、辺の比は１：２：√３。
ＥＨ＝１、ＡＨ＝√３
△ＡＢＨで三平方。
ＡＢ＝√（５²＋√３²）＝２√７
ＢＣ＝２√７ｃｍ
公立高校入試解説ページに戻る