平均59.3点(前年比;+7.9点)

問題はこちら→千葉日報さん
出題範囲の除外は標本調査。
大問1(計算)-91.1%
(1) 98.0%
-5×(-8)
=40
(2) 90.7%
-9+(-2)3×1/4
=-9-8×1/4
=-9-2
=-11
(3) 92.9%
(8a-5b)-1/3(6a-9b)
=8a-5b-2a+3b
=6a-2b
(4) 87.7%
2x+3y=7 …①
3x-y=-17 …②
①+②×3をすると、11x=-44
x=-4
①に代入。2×(-4)+3y=7
y=5
x=-4、y=5
(5) 89.1%
12/√6+√42÷√7
=2√6+√6
=3√6
(6) 88.0%
x2+9x+7=0
解の公式を適用。
x=(-9±√53)/2
大問2(小問集合)-55.7%
(1) 78.9%
ア:0×3+1×5+2×6+3×3+4×2+5×1=39冊×
イ:最頻値(モード)は最もあらわれている値で2冊×
ウ:20人の中央値(メジアン)は10番目と11番目の平均→2冊〇
エ:39÷20=2冊未満。平均値より大きい2冊以上は6+3+2+1=12人×
ウ
(2) 47.0%
切ったリボンは3bm。
残りはa-3bmで、これが5m以下。
a-3b≦5
(3) 52.7%
上と下は半径4cmの円。
側面積は縦8cm、横が底面の円周の長さ8πcmである長方形。
4×4×π×2+8×8π
=96πcm2
(4) 60.7%
bに4以上を入れると分子<分母になってしまい、整数にならない。
bは3以下。
◆b=3のとき
a+1=6
a=5
◆b=2のとき
a+1=4
a=3
◆b=1のとき
a+1=2、4、6(*約分した整数は1、2、3)
a=1、3、5
計5通り、確率は5/36
(5) 39.2%(無答18.4%)
だいぶ易化です。
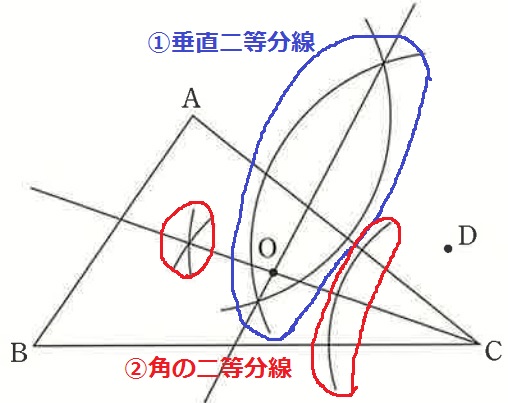
①円の中心OはADから等距離→ADの垂直二等分線上のどこか。
②円OはAC、BCに接する→ACとBCから等距離(半径と接線は垂直)
→∠ACBの二等分線上のどこか。
2本の線の交点がOとなる。
大問3(関数)-36.3%
(1) 78.9%
y=1/2x2に各々のx座標を代入する。
A(-2、2)⇒B(4、8)
右に6、上に6だから傾きは1。
Aから右に2、上に2移動して切片は4。
y=x+4
(2)① 29.5%!
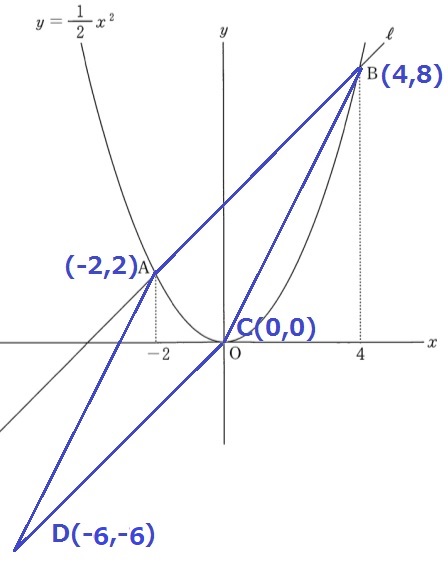
B⇒Aは左に6、下に6移動するので、
Cから出発して同様に移動するとD(-6、-6)
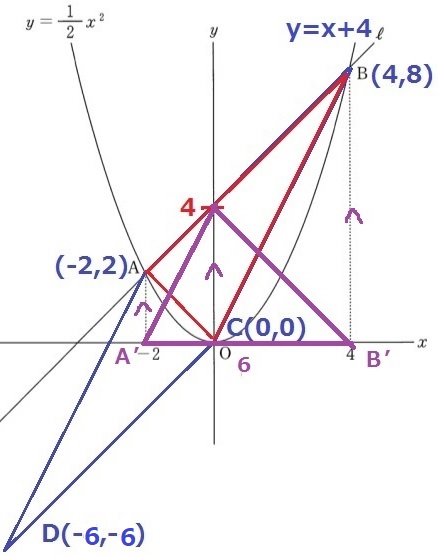
しかし、面積を出すのにD座標は不要である。
対角線AOで切ると△AOBが平行四辺形の半分なのだから、これを2倍すればいい。
△AOBは幅6高さ4→平行四辺形の面積は、6×4÷2×2=24cm2
② 2.5%!!
シンプルながらもやりづらい:;(∩´_`∩);:

もし、AとD、BとCのx座標が同じであった場合、
上図のように考えると、AD=15÷6=5/2cm
ABとDCは平行ゆえ傾きが等しい。
DCはABをy軸方向に-5/2平行移動した直線である。
DCの切片は、4-5/2=3/2
DC;y=x+3/2
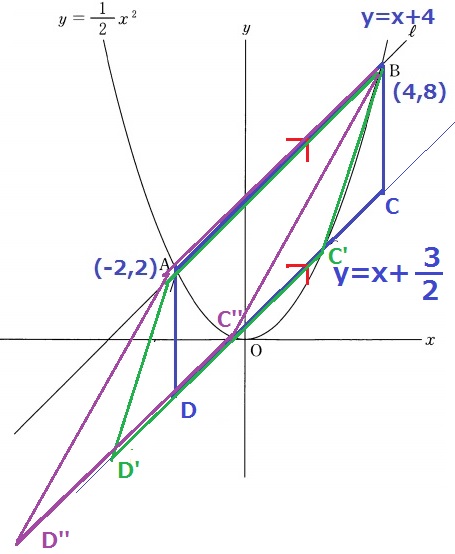
辺DCをy=x+3/2上で平行移動させると、平行四辺形ABCDの等積は維持される。
あとはCをy=1/2x2に乗せればいい。
すなわち、Cはy=1/2x2とy=x+3/2の交点となる。
1/2x2=x+3/2
x2-2x-3
=(x+1)(x-3)=0
-2<x<4より、x=-1、3
◆Cのx座標が-1
y=x+3/2に代入して、C(-1、1/2)
AとBのy座標の差が6だから、CとDのy座標の差も6。
Dのy座標は、1/2-6=-11/2
◆Cのx座標が3
同様に、C(3、9/2)
Dのy座標は、9/2-6=-3/2
答えは、-3/2、-11/2
大問4(平面図形)-54.5%
(1)a…88.7%、b…88.6%、c…6点―37.2%、3点―3.9%、無答―30.3%
△ACD∽△DBOの証明。
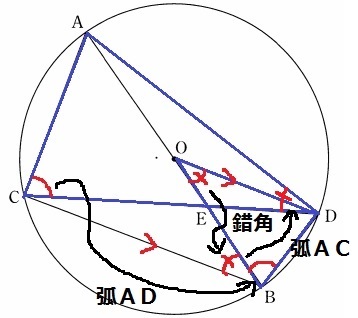
弧ADに対する円周角で、∠ACD=∠DBO
CB//ODより、錯角で∠ABC=∠DOB
弧ACに対する円周角で、∠ABC=∠ADC
2角が等しく∽
a…ウ、b…エ、c…上記参照
(2) 3.4%!!
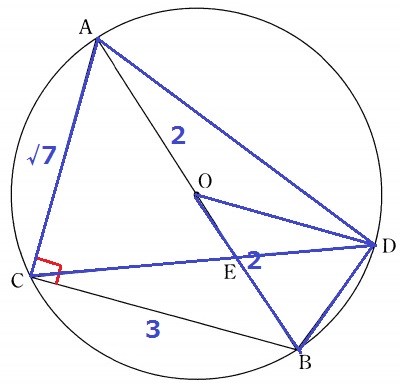
半円の弧に対する円周角より、∠ACB=90°
△ABCで三平方→AC=√7cm
角度の情報が乏しいので、前問の△ACD∽△DBOを活用して、
△ACDと△DBOの面積比を求める。
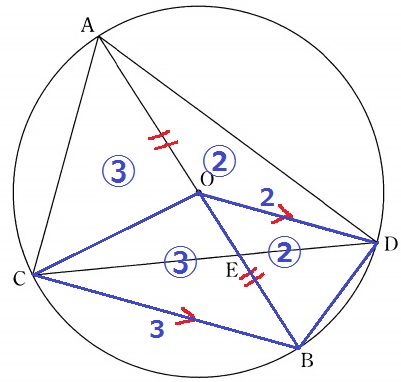
OCに補助線。
OD//CBより、台形OCBDの上底と下底の比から、
△DBOの面積を②とおくと、△CBOの面積は③
半径でAO=OBなので、△CAO=△CBO=③
△DAO=△DBO=②
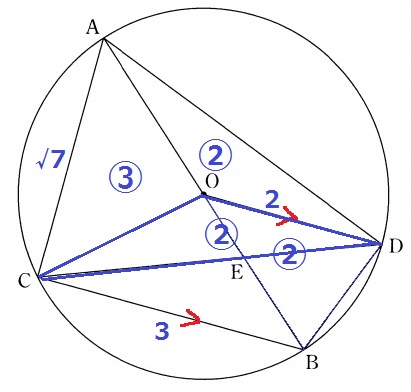
等積変形で△DCO=△DBO=②
△ACD:△DBO=⑦:②
相似比は√7:√2でAC=√7cmだから、これに対応するBD=√2cm
大問5(規則)-49.3%
(1)ア 88.5%
1段目の最大数…4
2段目の最大数…8
3段目の最大数…12
n段目の最大数…4n
イ 74.4%
同じ段の最大数から-3をすれば、その段の最小数になる。
(1段目であれば4-3=1、2段目であれば8-3=5)
n段目の最小数は4n-3
(2)4点―20.0%、2点―15.3%、無答―40.0%!
説明問題。
m段目の最小数…4m-3
n段目の2番目の数…4n-1(最大数4nから1を引いた数)
(4m-3)+(4n-1)
=4m+4n-4
=4(m+n-1)
m+n-1が整数なので、4(m+n-1)は4の倍数である。
したがって、m段目の最小の数と、n段目の2番目に大きい数の和は4の倍数である。
(3) 6.5%!!
B列縛りがきたので、条件に合う数が何段目にくるのか調べる。
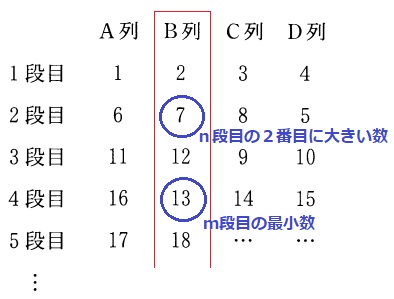
最小数がB列にくる、初めの段は4段目。
数字の順序は4の倍数ごとで同じだから、4、8、12…と続く。
→B列が最小の数となるのは4m段目。
前問でm段目の最小の数が4m-3だったから、
4m段目の最小の数は、4×(4m)-3=16m-3
2番目に大きい数がB列にくる、初めの段は2段目。
2、6、10、14…と続く→2+4(n-1)=4n-2段目
前問でn段目の2番目に大きい数が4n-1だったから、
4n-2段目の2番目に大きい数は、4(4n-2)-1=16n-9
(16m-3)+(16n-9)
=16m+16n-12
=12(m+n-1)+4m+4n
最後の4m+4nが12の倍数であれば、
12(m+n-1)+4m+4nは全体で12の倍数となる。
【4m+4n=12の倍数】
条件に合うn段目は4n-2段目なので、4nを4n-2にチェンジすると…
【4m+(4n-2)=12の倍数-2】 ←両辺を-2
0<4m,4n-2<20
0<4m+(4n-2)<40
40未満で〔12の倍数-2〕である整数は10、22、34しかない。
◆4m+(4n-2)=10
4mは4の倍数、4n-2は4の倍数ではない2の倍数。
4の倍数で場合分けするのが良いと思います。
(4m、4n-2)=(4、6)(8、2)
◆4m+(4n-2)=22
(4m、4n-2)=(4、18)(8、14)(12、10)(16、6)
◆4m+(4n-2)=34
(4m、4n-2)=(16、18)
以上、7組。
@別解@
YAさんから素晴らしい解法を頂きました。
B列が最小となる数のm段目は4、8、12、16段目。
B列が2番目に大きい数となるn段目は2、6、10、14、18段目。
よく見ると、互い違いに偶数段しかあらわれません。
(2)でm段目の最小の数4m-3とn段目の2番目に大きい数4n-1の和は
4(m+n-1)だったので、(m+n-1)が3の倍数になれば12の倍数となります。
mの最小が4、最大が16。nの最小が2、最大が18。
mとnはともに偶数なので、m+n-1の値は奇数。
つまり、6≦m+n≦34の範囲で、かつm+n-1が奇数である3の倍数を調べます。
◆m+n-1=9のとき
m+n=10
(m、n)=(4、6)(8、2)
◆m+n-1=15のとき
m+n=16
mが4の倍数で、nが4の倍数ではない2の倍数ですから、
m+nは4の倍数ではない2の倍数でなければおかしいです。×
◆m+n-1=21
m+n=22
(m、n)=(4、18)(8、14)(12、10)(16、6)
◆m+n-1=27
m+n=28
先ほどと同様で×。
◆m+n-1=33
m+n=34
(m、n)=(16、18)
したがって、7組となります。
*こちらの解法のほうが前問の解答を活かしています。
●講評●
大問1
各5点、合計30点。
どれも基本。ミスがこわい。
大問2
ここもミスがこわい。
(4)b=1のときは3通りある。
(5)作図もよくある形式。
大問3
(2)①平行四辺形の対角線は二等分する。
②平行四辺形を等積変形させるイメージ。
AB//DCかつAB=DC。DCはABと平行な直線上のどこかにある。
ABの真下にDCがある場合を想定して、DCを含む直線の切片を算出する。
大問4
(2)前問の相似を利用する。解説では中学受験の算数的手法で面積比を出した。
大問5
(2)文字式に変換すれば、あとはお馴染みのやり方。
(3)規則に整数が絡み、難関私立さながらの難問であった(;´・ω・)
前問の利用だがB列縛りがキツイ。
該当するmは4つ、nは5つしかないので、
下手に一般化せず、9つの数字を洗い出してしまうのも手。
@2021年度千葉解説@
社会…平均59.3点 理科…平均54.6点 英語…平均61.7点 国語…平均52.8点
思考力を問う問題(サンプル)…初年度は県立千葉のみ実施。



コメント
大した問題ではないですが、大問3(2)①のDの座標が間違ってると思います。D(-6,-10)ではないでしょうか。
コメントありがとうございます(*’ω’*)
ああ~!!平行線で違うところを見ておりました。
D(-6、-6)ですね。
修正しておきました。お知らせ頂き、感謝でございますm(_ _)m
大問4の3ですが
線分OEと線分EBの比が2:3
OBが2㎝なので
OEの長さは4/5
EBの長さは6/5
三角形ACEと三角形DBEは相似かつAC=√7
三角形ACEと三角形DBEの比が7:3
AC=√7なので
3/7√7
△ACE∽△DBEのところですが、
AEに対応する辺はDEですね。
弧BCに対する円周角より、∠CAE=∠BDEですので。
大問4の3
△EDO∽△ECBで、相似比は2:3なのでED:ECは2:3
△EBDの面積を2Sとすると△EBCの面積は3S
AO:OE:EBは5:2:3なので△ECAの面積は△EBCの7/3倍で7S
したがって△ECAと△EBDの面積比は7:2
△ECA∽△EBDでCA=√7、BD=xとすると、相似比と面積比の関係から
7:x2=7:2
x=√2
私も問題の流れから△ACD∽△DBOに注目しましたが、
上記の方法なら補助線もいらず計算も容易だと思います
大問4の3 別解
△EDO∽△ECBで、相似比は2:3なので、OE:EBは2:3
AO=OBなので、AO:OE:EBは5:2:3
AEはABの7/10倍なので14/5cm、OEはABの2/10倍(OBの2/5倍)なので4/5cm
△AED∽△DEOより、14/5:ED=ED:4/5
これを解いてEDは(2√14)/5cm
△AEC∽△DEBで相似比は14/5:(2√14)/5、これを簡単にして7:√14
このまま計算してもできますが、7=√49で√7で両方割れば、√7:√2
三平方の定理CAは√7cmなので、BAは√2cm
√の仕組みがわかっていれば、最初の計算で4と14をかける必要はなく計算は簡単です
同様に7:√14を使って計算してもそれほど面倒ではないと思います
中学生でもわかるように書いたつもりです
コメントありがとうございます。
私の解法は△ACDを3つに分解するのでわかりづらく、
山形県在住さんのように△EBCを経由の方したがスッキリしてますね!
△AED∽△DEO用いた別解も新たな発見でした。ありがとうございますm(_ _)m
大問4.3
単純に求めるBD=Xとおき、直角△ABDにピタゴラを適用すると、AD=√(16-X^2)
直角△ABCのピタゴラからAC=√7
前問の相似より、AD:AC=OB:BD
OB=2を含めて代入し、X√(16-X^2)=2√7を得る
これを解くとX^2=2、14ゆえX=√2、√14となるが、√14は不適ゆえX=√2
*ピタゴラはあまり好きではないですが試験の本番で長さを求めるのに面積比から入っていく難しさを考えると、こういう直接的な解法の方が実践的では?とも思います