2022年度　東京都立高校入試問題過去問・分割後期【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
７＋６×（－２/３）
＝７－４
＝３

（２）
（９ａ－１）/８－（ａ－５）/４
＝｛（９ａ－１）－２（ａ－５）｝/８
＝（９ａ－１－２ａ＋10）/８
＝（７ａ＋９）/８

（３）
（√６－３）（√６＋２）
＝６＋２√６－３√６－６
＝－√６

（４）
８ｘ－７＝４ｘ＋１
４ｘ＝８
ｘ＝２

（５）
２ｘ＋ｙ＝９　…①
ｘ＋３ｙ＝７　…②
②×２－①をすると、５ｙ＝５
ｙ＝１
②に代入、ｘ＋３＝７→ｘ＝４
ｘ＝４、ｙ＝１

（６）
ｘ²＋14ｘ＋45
＝（ｘ＋９）（ｘ＋５）＝０
ｘ＝－９、－５

（７）
ｙ＝－１/３ｘ²は上に凸のグラフ。
ｘ＝０のとき、最大値ｙ＝０
ｘ＝－３のとき、最小値ｙ＝－３
－３≦ｙ≦０
①…ア、②…エ

（８）
５枚から２枚取る組み合わせ→₅Ｃ₂＝10通り
大きい数と小さい数が３以上離れる組み合わせは、
（５、１）（５、２）（４、１）の３通り。
確率は３/10
あ…３、い…１、う…０

（９）

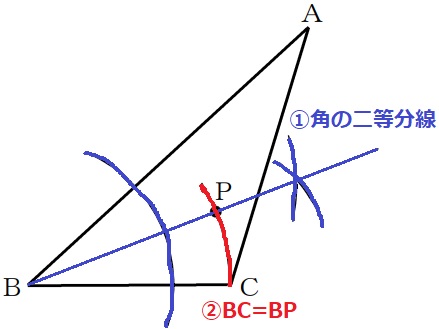
①ＡＢとＢＣまでの距離が等しい→∠ＡＢＣの二等分線
②ＢＣ＝ＢＰ

大問２（式の証明）

（１）

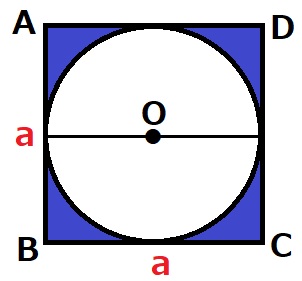
１辺ａの正方形から直径ａの円をひく。
ａ²－π（ａ/２）²
＝ａ²－πａ²/４
＝ａ²（１－π/４）
ア

（２）

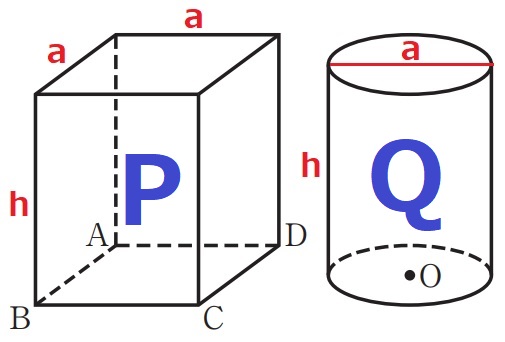
各々の表面積を算出。
Ｐ＝ａ²×２＋ａｈ×４
＝２ａ²＋４ａｈ
πＰ/４＝π（２ａ²＋４ａｈ）÷４
＝π（１/２ａ²＋ａｈ）　…①

Ｑ＝π×（１/２ａ）²×２＋πａｈ
＝１/２πａ²＋πａｈ
＝π（１/２ａ²＋ａｈ）　…②
①、②より、Ｑ＝πＰ/４

大問３（関数）

（１）
Ｐは直線ℓ上の点。
ｙ＝ｘ＋２にｘ＝－５を代入して、
ｙ＝－５＋２＝－３
ウ

（２）①

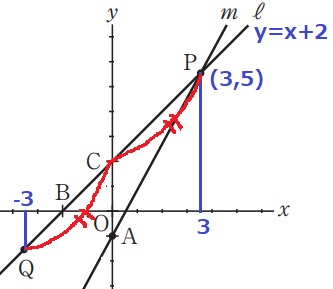
Ｑのｘ座標が－３でＰＣ＝ＣＱだから、Ｐのｘ座標は３。
ｙ＝ｘ＋２にｘ＝３を代入して、Ｐ（３、５）
Ａ（０、－１）⇒Ｐ（３、５）
右に３、上に６だから、傾きは６/３＝２
イ

②

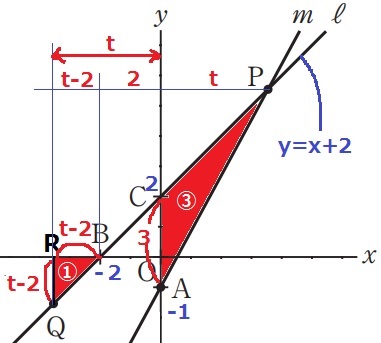
Ｐのｘ座標をｔとおく。
（以下、三角形の面積は÷２を省いている）
△ＡＰＣ＝３ｔ
Ｒのｘ座標は－ｔ。
ＲＯの距離がｔだから、ＲＢ＝ｔ－２
ｙ＝ｘ＋２の傾きは１（45度線）なので、△ＢＲＱは直角二等辺。
ＲＱ＝ｔ－２
△ＢＲＱ＝（ｔ－２）²

△ＡＰＣ＝△ＢＲＱ×３
３ｔ＝３（ｔ－２）²←÷３
ｔ＝（ｔ－２）²
ｔ²－５ｔ＋４
＝（ｔ－４）（ｔ－１）＝０
ｔ＞２ゆえ、ｔ＝４
Ｐのｘ座標は４。

大問４（平面図形）

（１）

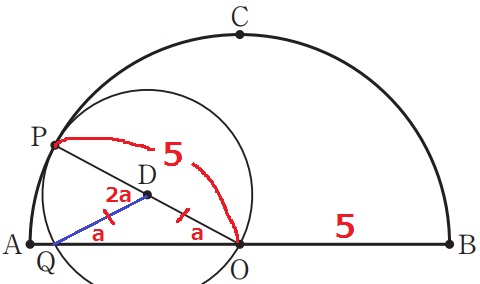
円Ｄの半径からＤＯ＝ＤＱ、△ＤＯＱは二等辺三角形。
∠ＤＱＯ＝∠ＤＯＱ＝ａ
この外角定理で、∠ＰＤＱ＝２ａ

ＰＯは円Ｏの半径で５ｃｍ。
ＰＱ＝５×π×２ａ/360＝πａ/36ｃｍ
エ

（２）①
△ＡＢＰ∽△ＡＰＱの証明。

共通角で、∠ＢＡＰ＝∠ＰＡＱ
半円の弧に対する円周角で∠ＡＰＢ＝90°
∠ＯＱＰ＝90°→∠ＡＱＰ＝90°
２角が等しいから∽

②

前問で△ＡＢＰと△ＡＰＱが相似関係にある直角三角形とわかった。
●＋×＝90°の角度調査でさらに展開すると、△ＡＰＱ∽△ＰＢＱ（∽△ＡＢＰ）。
ＡＱ：ＱＰ＝ＰＱ：ＱＢ
ＱＢ＝②×２＝④

ＡＢ＝⑤＝10ｃｍ
①＝２ｃｍ

弧ＡＣ＝弧ＣＢより、Ｃは半円の弧の中点、つまりＯの真上にある。
∠ＣＯＢ＝90°

△ＰＢＱの面積は、８×４÷２＝16ｃｍ²
△ＰＢＱ∽△ＲＢＯより、ＲＯ＝４×５/８＝５/２ｃｍ
台形ＯＲＰＱの面積は、（４＋５/２）×３÷２＝39/４ｃｍ²
え…３、お…９、か…４

大問５（空間図形）

（１）

ＡＱ＝ＡＤ＝ＣＱ＝ＣＤ＝８ｃｍ、共通辺ＱＤ
３辺の長さが等しいので、△ＡＱＤ≡△ＣＱＤ。
∠ＱＡＤ＝∠ＱＣＤ＝90°（△ＡＱＤは直角二等辺三角形）
△ＡＱＰで三平方→ＰＱ＝４√５ｃｍ
き…４、く…５

（２）

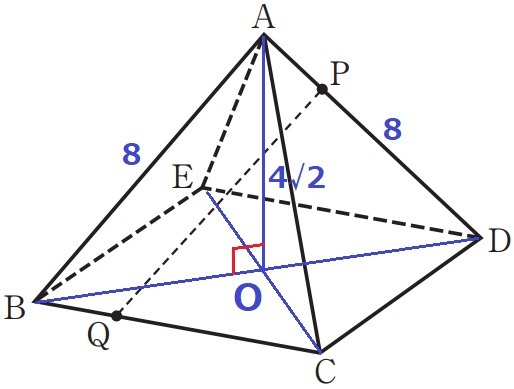
はじめに正四角錘Ａ－ＢＣＤＥの高さを出しておく。
正方形ＢＣＤＥの対角線の交点をＯとすると、高さはＡＯにあたる。
前問より△ＡＢＤは直角二等辺三角形→△ＡＢＯも直角二等辺。
辺の比は１：１：√２で、ＡＯ＝８×１/√２＝４√２ｃｍ

三角錐Ａ—ＱＤＥの体積は正四角錘の半分である。
なぜなら、高さが等しく、底面の△ＱＤＥは等積変形すると正方形ＢＣＤＥの半分だから。

ＡＰ：ＰＤ＝６：２＝③：①
三角錐Ａ—ＱＤＥの体積を④とすると、高さの比から三角錐Ｐ―ＱＤＥは①。
ということは、求積すべき立体Ｑ—ＡＥＰの体積は③となる。
８×８÷２×４√２÷３×③/④＝32√２ｃｍ³
け…３、こ…２、さ…２

＠2022年度・都立解説＠
数学…平均59.0点　社会…平均49.2点　理科…平均61.4点　英語…平均61.1点
公立高校入試解説ページに戻る