2019年度　徳島県公立高校過去問【数学】解説

平均46.1点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－５＋２＝－３

（２）
（ｘ＋２）²
＝ｘ²＋４ｘ＋４

（３）
反比例の一般式：ｙ＝ａ/ｘ
比例定数ａ＝３
ｙ＝３/ｘ

（４）
ｎ角形の内角の和→180（ｎ－２）
180×（５－２）＝540°

（５）
２ｘ²－ｘ
＝ｘ（２ｘ－１）＝０
ｘ＝０、１/２

（６）
2.4＜√ａ＜３
２乗して根号を外す。
5.76＜ａ＜９
自然数ａ＝６、７、８。

（７）
すべての場合→２⁴＝16通り
600円以上となるには、500円と100円は必ず表。
この２枚は表で固定。残りの50円と10円は何でもいい。
50円と10円の出し方は、２²＝４通り
よって、４/16＝１/４

（８）
Ｐはｘ軸との交点なので、ｙ座標は０。
Ｐのｘ座標を求める。
６ｘ－０＝10
ｘ＝５/３
Ｐ（５/３、０）

ａｘ－２ｙ＝15に代入。
５/３ａ－２×０＝15
ａ＝９

（９）
扇形の半径（母線）：底面の円の半径＝円の中心角：扇形の中心角
半径の比の逆比が、角度の比にあたる。
円の半径…16×135/360＝６ｃｍ

（10）
100の中央値（メジアン）は50と51番目の平均値。
ａ＋ｂ＝100－（23＋15＋６）＝56
ａ…56×４/７＝32
23＋32＝55
50と51番目は、ともに10以上～20未満の階級にある。
よって、相対度数は、32÷100＝0.32

大問２（空間図形）

（１）
辺ＡＤと平行な辺は、三角柱の高さにあたる。
辺ＢＥ、辺ＣＦ

（２）
△ＡＢＣで１：１：√２の直角三角形。
ＢＣ＝10√２ｃｍ

（３）ａ
面積比は辺の比の２乗。

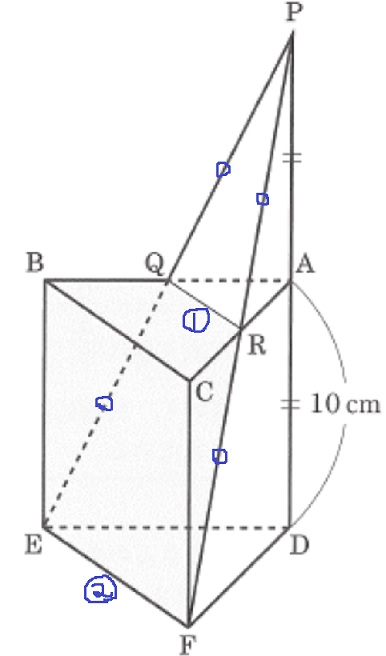
辺の比は１：２なので、△ＰＱＲは△ＰＥＦの１/４倍。

ｂ
体積比は辺の比の３乗。

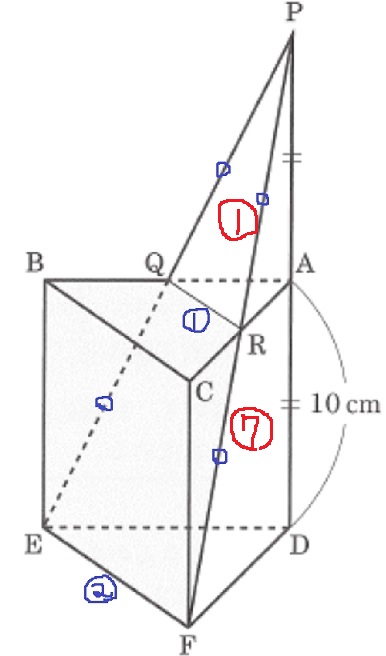
三角錐Ｐ－ＤＥＦにおいて、上：下＝１³：２³－１³＝１：７
下（ＡＱＲ－ＤＥＦ）＝10×10×１/２×20×１/３×７/８＝875/３ｃｍ³
三角柱ＡＢＣ－ＤＥＦからこれをひく。
10×10×１/２×10－875/３＝625/３ｃｍ³

大問３（文字式）

（１）
ｘが高度ｋｍ、ｙが温度℃。
ｘに代入して、ｙの値の差を求める。
Ｐ：ｙ＝18－６×1.5＝９℃
Ｒ：ｙ＝18－６×2.1＝5.4℃
よって、９－5.4＝3.6℃低い。

（２）ａ
秒を分に変換する。
５秒→５/60＝１/12分
20秒→20/60＝１/３分
ア…１/12、イ…１/３

イスの速さを分速ｘｍ、イスの間隔をｙｍ。
ｙは距離で、速さ×時間＝距離から等式を立てる。

↑ｙの距離で立式。
■出会う
１/12×48＋１/12ｘ＝ｙ
１/12ｘ＋４＝ｙ…①

■追い越す
１/３ｘ－１/３×48＝ｙ
１/３ｘ－16＝ｙ…②
ウ…１/12ｘ＋４、エ…１/３ｘ－16

ｂ
①、②を解く。
１/12ｘ＋４＝１/３ｘ－16
ｘ＝80、ｙ＝32/３
イスの速さは分速80ｍ、イスの間隔は32/３ｍ。

＠別解＠
速さで等式を立てることもできる。
イスの速さを分速ｘｍとおく。
出会いで５秒、追い越しで20秒。
時間の比が１：４、速さの比は逆比で４：１。
出会いの速さの和＝追い越しの速さの差×４
48＋ｘ＝４（ｘ－48）
ｘ＝80

大問４（関数）

（１）
ｙ＝ｘ²に放り込むのみ。
ｙ＝２²＝４
A（２、４）

（２）
同様に、Ｂ座標を求める。
Ｂ（３、９）
Ｐ（０、６）⇒Ｂ（３、９）
右に３、上に３なので、傾きは１。
ｙ＝ｘ＋６

（３）
ｙ＝２ｘ²のとき、Ａ（２、８）Ｂ（３、18）Ｃ（－１、２）

↑なんか点の位置がおかしいが。。
お馴染みの等積変形。ＡＢ//ＣＰで傾きが等しくなる。
（Ａ⇒Ｂ）右１上10。
（Ｃ⇒Ｐ）右１上10。Ｐ（０、12）
よって、Ｐのｙ座標は12。

（４）
反射の問題→線対称
ｙ軸を対称の軸とし、Ｂを左へ対称移動させた点をＢ’とおく。

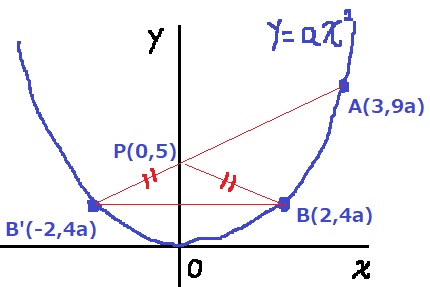
ＰはＡＢ’とｙ軸の交点にあたる。
Ａ（３、９ａ）Ｂ’（－２、４ａ）
ＡＢ’の傾きは、右に５、上に５ａ→ａ

ＡＢ’の直線の式は、ｙ＝ａｘ＋５
ｘ＝３、ｙ＝９ａを代入。
９ａ＝３ａ＋５
ａ＝５/６

大問５（平面図形）

ラグビーワールドカップを題材にした設問。
（１）
総当たり戦（リーグ戦）の試合数。

５チームなので、５－１＝４⇒１～４までの総和。
10試合

（２）ａ
トライ後に五郎丸選手がお馴染みのルーティーンで蹴るアレ。
トライした位置の延長線であれば好きな場所から蹴れるらしい。
コンバージョンゴールというそうで、ゴールポストから離れるほど（端にいくほど）難易度が高くなる。
（だから、余裕があるときは中央に寄ってトライを決める）
本問は円の中心Ｏの作図。
Ａ・Ｂ・Ｐ’が円の円周上にくるので、これらのうち２つを選び、垂直二等分線を作成。
２本の垂直二等分線の交点がＯとなる。

ｂ
接点Ｐ’を円周角とする角が最大角となる理由。
特殊な証明だが、そんなに難しくない。

円周角の定理より、∠ＡＰ’Ｂ＝∠ＡＲＢ（●）
△ＢＲＱに注目！
外角定理から、∠ＡＲＢ（●）＝∠ＲＢＱ（●）＋∠ＡＱＢ（●）
∠ＡＲＢ＞∠ＡＱＢだから、∠ＡＰ’Ｂ＞ＡＱＢとなる。

＠まとめ＠

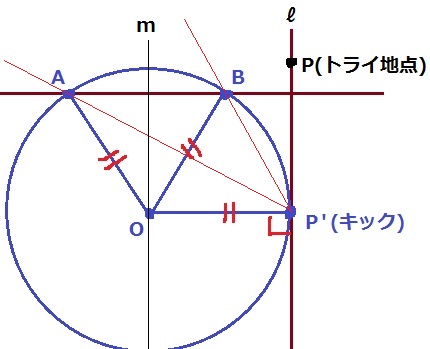
Ａ・Ｂ・ℓはわかっているので、キッカーが蹴るべきＰ’は円の中心Ｏの真横となる。
ＯはＡとＢの垂直二等分線（ｍ：ゴールの真ん中）のどこかにあり、Ｐ’はℓのどこかにある。
作図では、ｍとℓの距離をとり、これをＢに針を移してｍとの交点がＯ。
Ｏを通るℓとの垂線をひき、交点がＰ’となる。
公立高校入試解説ページに戻る