平均69.8点
問題はコチラ→ＰＤＦファイル（Ａ問題の次です）
大問１（小問集合）
（１）ア
７－（－２）3
＝７－（－８）
＝７＋８＝15
イ
√32－√２
＝４√２－√２
＝３√２
ウ
ａ－（２ａ－ｂ）/３
＝（３ａ－２ａ＋ｂ）/３
＝（ａ＋ｂ）/３
（２）
（ｘ＋１）2＝５
ｘ＋１＝±√５
ｘ＝－１±√５
（３）
傾きａは正なので、①は右上がり、②は下に凸のグラフになる。
①ア②エ
（４）
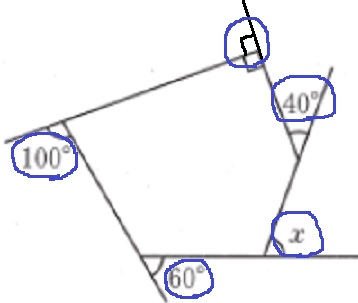
多角形の外角の和は360°だから、
ｘ＝360－（90＋100＋60＋40）＝70°
（５）
標本調査。解答では簡易な説明が求められる。
標本50個のうち、34個がＭサイズ。
この割合は母集団850個でも等しいとみなす。
850×34/50＝578個
（６）
菱形の作図。
まずは∠Ａ＝45°をつくり、ＡＢの長さをとって１つの頂点を確定する。
①Ａを通るＡＢに垂直な線分。
②その角の二等分線。
③ＡＢの長さを二等分線上に移して１つ確定。
④上の点とＢからＡＢの長さで交点を描き、菱形をつくる。
大問２（確率）
（１）
ルールの確認。
白２つが右側に移動する。
１回目→〇〇●●〇
２回目→〇●●〇〇
（２）
カードの取り出し方→５×５＝25通り
黒の碁石が隣り合わない場合を考える。
初期状態：〇〇〇●●
黒を入れ替えても同じなので、３つの白のうち１つを入れ替える。
１回目終了：〇〇●●〇
黒が隣り合ってはいけないので、２つの黒から１つを入れ替える。
２回目終了：〇〇●〇●
６通り。
したがって、確率は６/25。
大問３（文字式）
（１）
表の穴埋め。
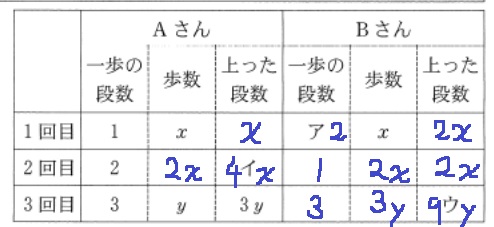
一歩の段数×歩数＝上がった段数
ア：２ イ：４ｘ ウ：９ｙ
（２）
Ａの歩数の合計は93歩。
ｘ＋２ｘ＋ｙ＝93
３ｘ＋ｙ＝93 …①
Ｂの上がった段数はＡよりも45段多い。
ｘ＋４ｘ＋３ｙ＋45＝２ｘ＋２ｘ＋９ｙ
５ｘ＋３ｙ＋45＝４ｘ＋９ｙ
ｘ－６ｙ＝－45 …②
連立を解いて、ｘ＝27 ｙ＝12
大問４（平面図形）
（１）
△ＡＤＦ∽△ＢＥＤの証明。
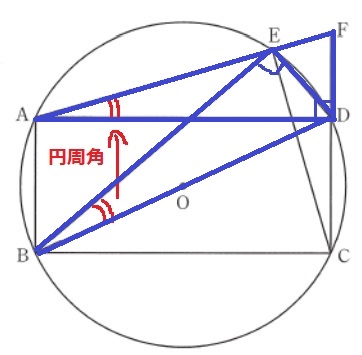
弧ＤＥに対する円周角→∠ＦＡＤ＝∠ＤＢＥ
半円の弧に対する円周角は90°＆長方形の外角
→∠ＦＤＡ＝∠ＤＥＢ
２角が等しく∽。
（２）ア
△ＤＢＣで三平方。
ＢＤ＝√（２√２2＋２2）＝２√３
Ｏの半径…２√３÷２＝√３ｃｍ
ＤＥは△ＢＥＤの１辺。
そこで、前問の△ＡＤＦ∽△ＢＥＤを利用する。
△ＡＤＦで三平方→ＡＦ＝３ｃｍ
ＦＤ：ＤＥ＝ＡＦ：ＢＤ＝３：２√３
ＤＥ＝１×２√３/３＝２√３/３ｃｍ
イ
ＢＣ＝２√２なので、この高さがわかればいい。
ＥからＢＣに向けて垂線をおろし、ＡＤとの交点をＧ、ＢＣとの交点をＨとする。
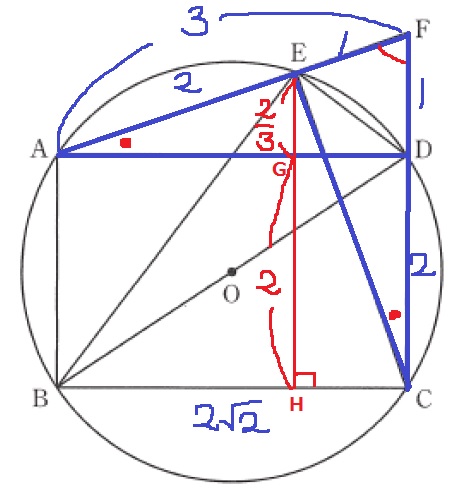
前問でＡＦ＝３ｃｍ。これがＣＦと同じ長さであることから、
△ＡＤＦと△ＣＥＦを調べてみると…
ＥＤに対する円周角と共通角、３ｃｍから１辺両端角で△ＡＤＦ≡△ＣＥＦ
ＥＦ＝１ｃｍ ＡＥ＝２ｃｍ
△ＡＥＧ∽△ＡＦＤから、
ＥＧ＝１×２/３＝２/３ｃｍ
ＥＨ＝２/３＋２＝８/３
よって、△ＢＣＥの面積は２√２×８/３×１/２＝８√２/３ｃｍ2
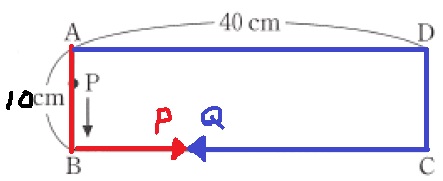
大問５（数量変化）
（１）
放物線は（10、160）を通る。
これをｙ＝ａｘ2に代入。
160＝100ａ
ａ＝８/５
ｙ＝８/５ｘ2
（２）
点Ｑが時計回り、反時計回りのいずれかであるかを説明した文の穴埋め。
解答→（線分ＡＱ、増加していく、同じ直線上、変化しない、時計）
Ｑが時計回りだと底辺と高さがともに増えていくので、
△ＡＰＱの面積ｙは倍々に増えていく。
Ｑが反時計回りだと、Ａ・Ｐ・Ｑが線分ＡＢ上にあるので△ＡＰＱが形成されない。
ｙの値は０のままとなるので、Ｑは時計回りとなる。
（３）
Ｑは時計回り。
グラフの折れ目である10秒後にＱはＤに着いた。
ＡＤ＝40ｃｍを10秒間で動くので、40÷10＝毎秒４ｃｍ
ＱはＤ～Ｃ間（ａｃｍ）を2.5秒で動く。
ａ＝４×2.5＝10ｃｍ
（４）
グラフの誤りを指摘して、その理由を説明するというユニークな設問。
12.5秒以降のグラフが誤りなので、ｙ＝０のときのｘ＝18が怪しい…。
12.5秒後にＰはＢ、ＱはＣにある。
ＰとＱは線分ＢＣ上で互いに近づいていき、どこかで出会う。
△ＡＰＱの面積ｙは次第に減っていき、ＰとＱが出会ったときに０となる。
出会ったとき、ＰとＱが動いた距離の合計は長方形の周りの長さである100ｃｍ。
12.5秒後でＰとＱが動いた距離の合計は10＋40＋10＝60ｃｍだから、
出会う時間は、12.5×100/60＝125/６秒後。
よって、グラフは（125/６、０）の点を通るので、（０、18）は通らない。
*公式解答のやり方は最短経路であり、他の方法でもｘ＝125/６を指摘できたら○です。
公立高校入試解説ページに戻る
コメント