平均57.57点(前年比;+9.52点)
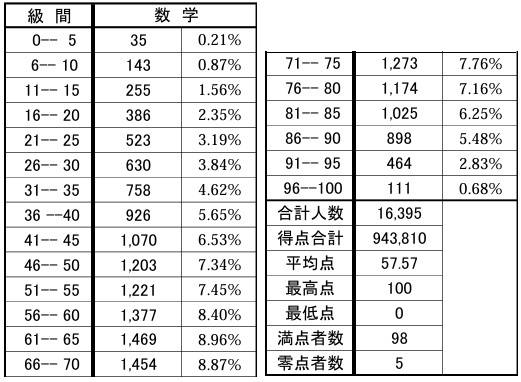
問題はこちら→産経新聞さん
大問1(計算)
(1)① 98.0%
3-9
=-6
② 86.3%
-3(x+2y)+(x-3y)
=-3x-6y+x-3y
=-2x-9y
③ 90.3%
3a2b×4b÷6ab
=2ab
④ 74.5%
√6(√2+√3)
=√12+√18
=2√3+3√2
(*√6=√2×√3と分解してかけてもいい)
(2) 88.0%
x2+7x-8
=(x-1)(x+8) 【エ】
大問2(小問集合)
(1) 68.9%
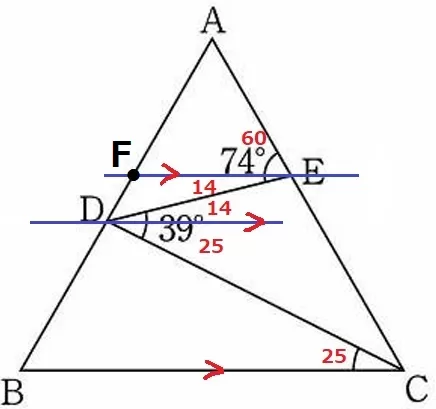
Eを通るBCに平行な線をひき、ABとの交点をFとする。
△AFE∽△ABC→△AFEも正三角形で∠AEF=60°
Dを通る平行線もひき、錯角でおろしていく。
74-60=14°、39-14=25° 【イ】
(2) 78.0%
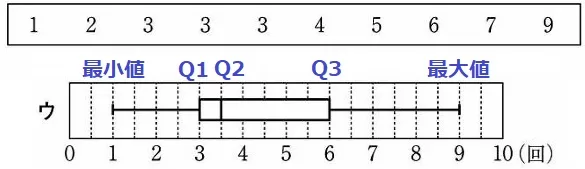
10人の中央値(Q2)は5番目と6番目の平均で3.5回。
第1四分位数(Q1)は下位5人の真ん中、下から3番目で3回。
第3四分位数(Q3)は上位5人の真ん中、上から3番目で6回。
以上を満たす箱ひげ図は【ウ】。
(3) 80.0%
大人2人…2x円、子供3人…3y円、割引券1枚使用で-500円。
これらの和が4000円より安いので、2x+3y-500<4000
【ア】
(4) 52.7%
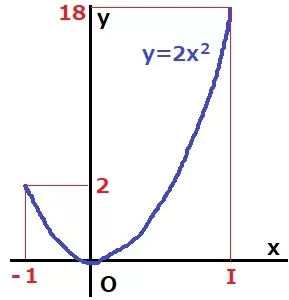
y=2x2は下に凸のグラフ。
x=-1のとき、y=2なので、
x=Ⅰ(Ⅰ>0)のときにy=18である。
18=2x2
x>0より、x=3(Ⅰ…3)
グラフは原点を通過するので、
x=0のとき、最小値y=0(Ⅱ…0)【エ】
大問3(平面図形)
(1) 89.4%
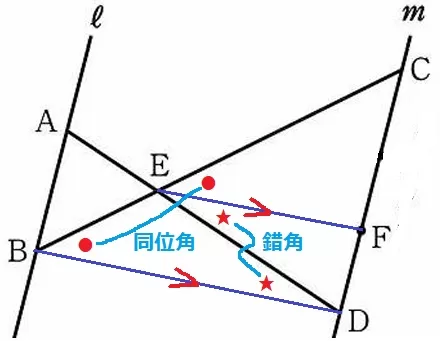
同位角で∠EBD=∠CEF【ア】
錯角で∠BDE=∠FED【オ】
(2) 17.3%!
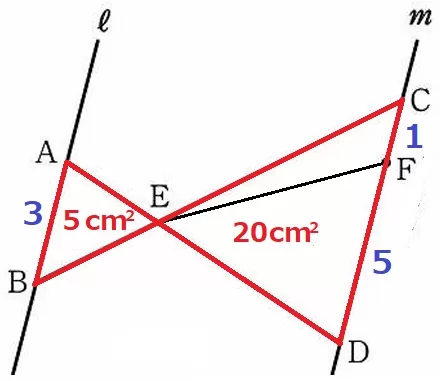
2角相等(対頂角・錯角)で△ABE∽△DCE
相似比は3:6=1:2
面積比は2乗して、△ABE:△DCE=1:4
△DCEの面積は、5×4=20cm2
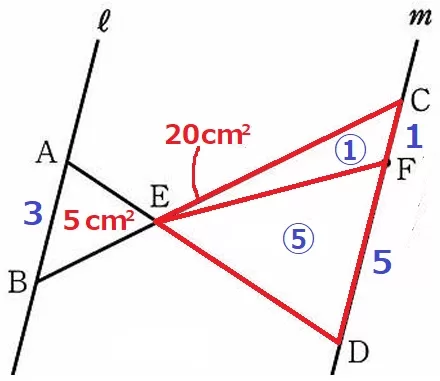
△DEF:△FEC=DF:FC=⑤:①
△DEFの面積は、20×⑤/⑥=50/3cm2
(3)Ⅰ-70.8%、Ⅱ-49.4%、Ⅲ-59.1%
△DCB≡△ECFの証明。
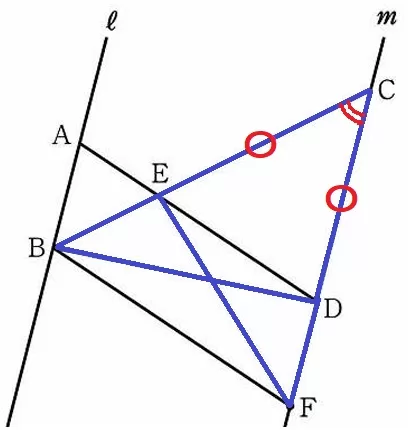
仮定より、CD=CE=6cm
共通角から、∠DCB=△ECF
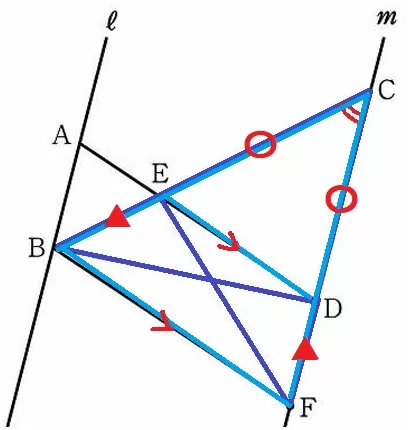
ここで△CBFに着目する。
ED//BFより、CE:CB=CD:CF
仮定のCD=CE(〇)→〇:CB=〇:CF→CB=CF(〇+▲)
2辺とあいだの角が等しいので合同。
Ⅰ…ウ、Ⅱ…CB=CF、Ⅲ…2辺とあいだの角
大問4(確率)
(1) 79.7%
a+bが3の倍数→3で割ると余りが0になる。
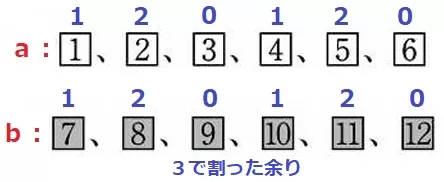
余りを調べると、(1・2・0)が連続する。
aで余り1を引いたら、bで余り2を引けばa+bは3の倍数になる。
aで余り2を引いたらbで余り1を、aで余り0を引いたらbで余り0を引けばいい。
つまり、aで何かを引いたら、それに対応する数をbで引けばいい。
対応するbの数はいずれも6枚のうち2枚。確率は2/6=1/3 【イ】
(2)① 56.1%
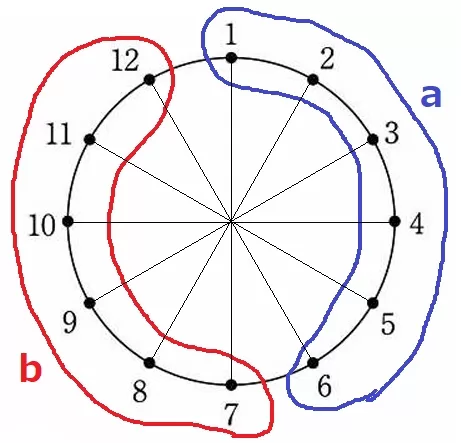
a側でどこかに置いたら、対応するbはaの反対側しかない。
(a=3はb=9、a=5はb=11)
対応するbの確率は1/6。
② 15.2%!
1は固定なので、aで1を引くと三角形にならない。(a≠1)
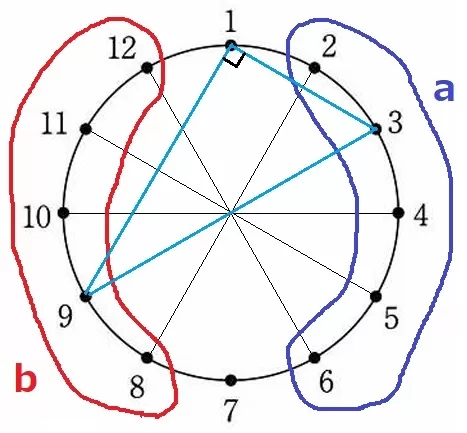
円周上の点を結んだ直角→円周角の定理で考える。
半円の弧に対する円周角は90°。直径と1を結ぶと直角三角形になる。
(1―7)のペアを除いた直径5本→5通り。
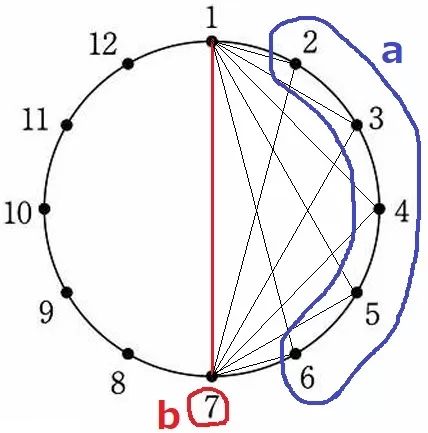
今度は、1が直径の一端である場合を考える。
直径は(1―7)、a=2~6の5通り。
計10通りで全体は6×6=36通りだから、確率は10/36=5/18
大問5(数量変化)
(1) 54.7%
水の体積は、100×60=6000cm3
これを底面積で割ればいい。
6000÷(30×20)=10cm
(2)① 66.6%
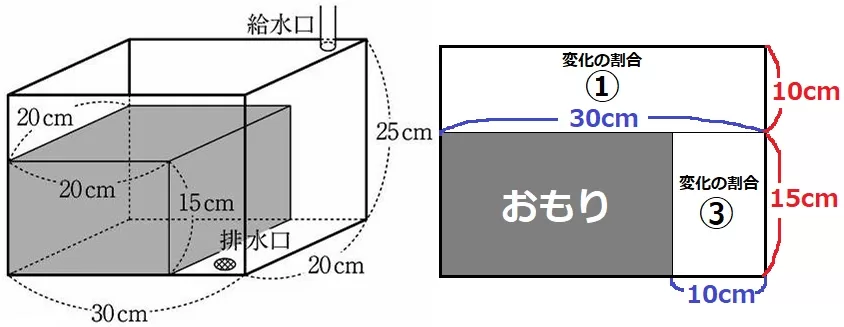
おもりは奥まであるので、正面から見た図の面積比がそのまま体積比になる。
おもりの高さ15cmで区切る。
高さ15cm以下の幅は10cm、高さ15cm以上の幅は30cm。
水は一定の割合で入るから、水面の高さの変化の割合は逆比で③:①。
(幅が1/3になれば、水面の上昇スピードは3倍になる)
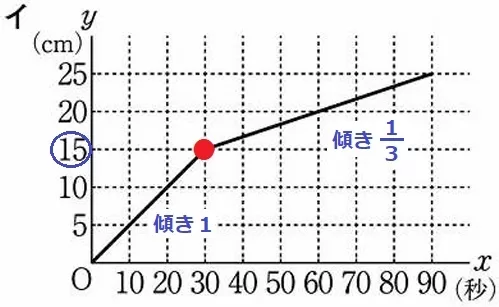
グラフの転換点は15cm→ア・イのどちらか。
15cm以下の方が変化の割合が大きいので【イ】と決まる。
念のため傾きを調べると、15cm以下は傾き1、
15cm以上は右に3、上に1だから傾きは1/3→変化の割合は③:①である。
② 12.3%!
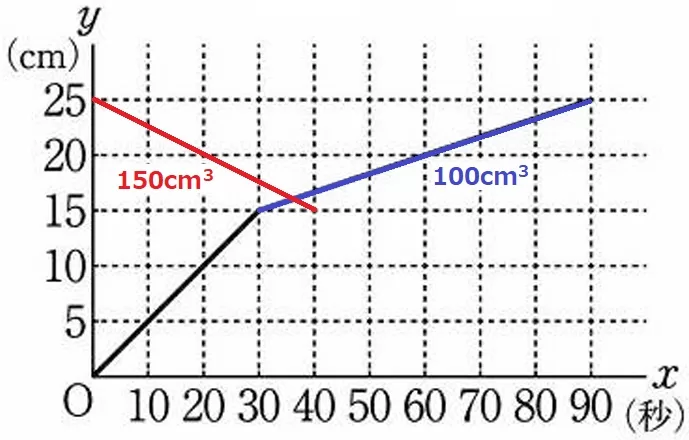
おもりの影響を受けない高さ15cm以上で考える。
給水;100cm3/秒では60秒かかっている。
排水;150cm3/秒では、60×100/150=40秒かかる。
つまり、排水のグラフは(0、25)と(40、15)を通過する。
求めるべき座標は2直線の交点である。
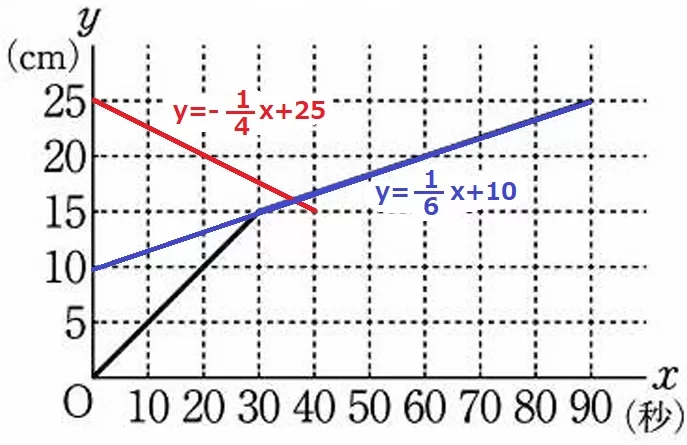
給水の傾き…右に30、上に5だから、5/30=1/6
延長すると切片はちょうど10なので、y=1/6x+10
排水の傾き…右に20、下に5cmだから、-5/20=-1/4
切片は25なので、y=-1/4x+25
1/6x+10=-1/4x+25 ←12倍
2x+120=-3x+300
x=36
y=1/6x+10にx=36を代入して、y=16
したがって、(36、16)
大問6(空間図形)
(1) 72.8%
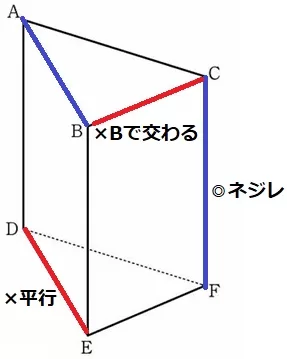
ねじれの位置…延長しても交わらない、かつ平行でもない(同一平面上にない)
ABとネジレなのはCFのみ。【オ】
(*他にはDFとEFがABとネジレである)
(2)① 28.8%!
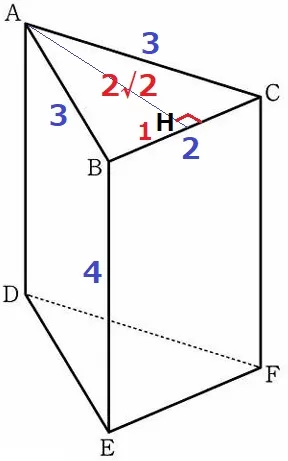
側面の3面を広げると、縦が4cm、横が3+3+2=8cmの長方形である。
底面は二等辺三角形。Aから垂線をひき、足をHとする。
△ABHで三平方→高さAH=2√2cm
表面積は、4×8+2×2√2÷2×2=32+4√2cm2
② 1.3%!!
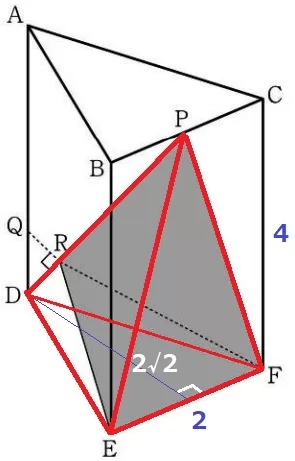
三角錐P―DEFの体積は、2×2√2÷2×4÷3=8√2/3cm3
高さの比であるDP:RPが知りたい。
ここで、∠QRD=90°を利用する。
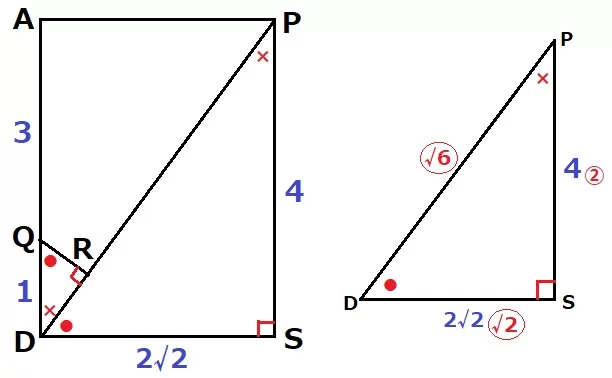
Pの真下をSとして、∠QRDを観察できる面ADSPで切り取る。
●+×=90°で角度を調査すると、△QDR∽△DPS。
DS:PS=2√2:4=〇√2:②
△DPSの辺の比で三平方→DP=〇√6
直角三角形の辺の比からDRとDPの長さを求めればいい。
DR=1×②/〇√6=√6/3cm
DP=4×〇√6/②=2√6cm
DR:DP=√6/3:2√6=①:⑥
したがって、求積すべき立体の体積は、8√2/3×⑤/⑥=20√2/9cm3
@別解@
DR:RPの比についてです。
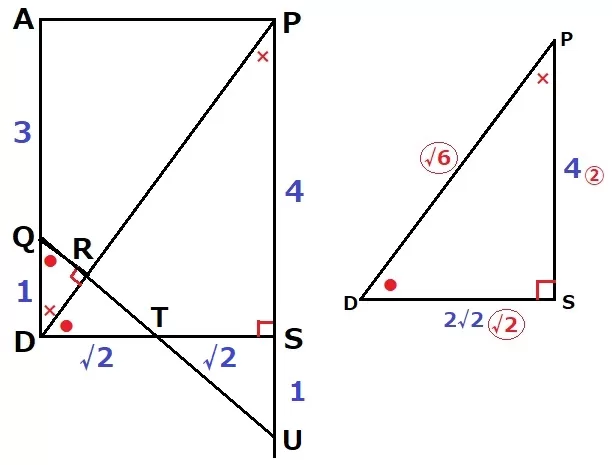
QRを延長しDSとの交点をT、PSの延長との交点をUとおいてみると…
DT=1×②/〇√2=√2cm→TはDSの中点である。
DT=STと等しい両端角から△QDT≡△UST
SU=1cm
△QDR∽△UPRより、DR:RP=1:5と求めることもできる。
●講評●
大問3までは点を稼ぎたい。後半の大問も2問目までは取りやすい。
大問1
配点20点。
大問2
配点20点。
(1)ジグザクの求角は平行線をひいて錯角。
初手は正三角形の60°を上にもってくる。
(3)移行の必要はなかった。
大問3
平面図形も解きやすい。
(3)穴埋め形式で、証明の流れから2辺と間の角と察しやすい。
大問4
(1)もちろん、3の倍数の数を調べ上げてもいい。
3の倍数がセットになっているので、aに対応するbだけを考えることもできる。
(2)②aで1を引くと2点のみで、三角形にならない。
b≠7では前問の直径を利用。b=7はaは1以外。
大問5
(2)①計算なしで選択できた。
②給水排水は速さと同じ。排水の量が多ければ、時間は逆比でかからなくなる。
直線が描ければ、式も出しやすい。
大問6
(2)②対応する辺を取り違えないように気を付けよう。
●×の等角を記すとミスを防ぎやすい。


コメント