大問1(小問集合)
(1) 98.3%
-7-(-5)
=-7+5
=-2
(2) 89.5%
-3/5+5/6
=7/30
(3) 95.7%
42-(-7)×2
=16+14
=30
(4) 95.1%
-3(a-b)+(4a-5b)
=-3a+3b+4a-5b
=a-2b
(5) 84.0%
√18-√32+3√8
=3√2-4√2+6√2
=5√2
(6) 47.7%
x2=x
x2-x=x(x-1)=0
x=0、1
(7) 87.9%
合計=平均×個数=3.6×10=36
□=36-(3+4+7+2+1+6+0+5+4)=4
(8) 53.2%
平行四辺形に惑わされないように・・。
折れ線はBとDの垂直二等分線となる。ウ
折れ線を対称の軸とした場合、BとDは対応する点となり、
軸からの距離が等しくなる。
大問2(方程式・確率)
(1)① 73.2%
製品①がx個、製品②がy個なので、それをかける。

② 25.0%!
部品Aは330個…6x+3y=330
部品Bは200個…2x+4y=200
これを連立で解くと、x=40、y=30
利益の合計は、60x+40y=60×40+40×30=3600円
(2)① 76.3%
同じカードには番号を振る。
仁のグー⇒正のグー1、グー2
仁のチョキ1⇒正のチョキ
仁のチョキ2⇒正のチョキ
仁のパー⇒正のパー
5通り
② 15.1%!
説明問題。
仁の勝率が正を上回る⇒仁の勝つパターンが正よりも多くなる。
最初のカードでは、仁の勝つパターンは、
仁グー⇒正チョキ
仁チョキ1⇒正パー
仁チョキ2⇒正パー
仁パー⇒正グー1
仁パー⇒正グー2
計5通り
カードの出し方は、4×4=16通り
あいこが5通り、仁の勝利が5通りなので、
正の勝利は16-5-5=6通り
正のほうが勝ちパターンが1つ多いので、仁より勝率が高くなる。
仁に1枚パーを追加すると、
仁パー2⇒正グー1
仁パー2⇒正グー2で勝ち、
仁パー2⇒正チョキで負ける。
2勝1敗なので、勝ちパターンが仁と正でイーブンとなる。
仁の勝率が正よりも初めて大きくなるのは、パーを2枚追加したとき。
大問3(総合問題)
(2) 28.6%!
循環小数は、数字が規則正しく、無限に並ぶ小数。
ア…4/3=1・1/3=1.33333・・・〇
イ…3/5=0.6×
ウ…√2が無理数なので、√2-1も無理数。×
エ…小数のうえに点がつくと、点~点までの数字が繰り返される。
本問では、0.121212121212…〇

オ…円周率πは3.14152965…と代表的な無理数。×
2019年度現在、日本人が円周率31兆4000億桁の計算に成功したらしい。。→BBC
グーグルのエンジニアだそうです。NASAが公開している円周率の使用方法リストでは、
- 火星の表面に惑星探査機を着地させるのに必要なパラシュートのサイズを計算する
- 地球の表面のマッピングに長方形カメラがいくつ必要なのかを導き出す
- 惑星の周りの軌道に突入するために宇宙探査機にブレーキをかける適切なタイミングを計る
(3) 30.1%!
√3の作図方法。空欄には△APQ∽△QPBの証明を埋める。

垂線の作図からAB⊥QP→直角
半円の弧に対する円周角は90°なので、○+×=90°から等しい角を指摘。
2角が等しい→∽
*△APQ∽△QPBより、
1(AP):PQ=QP:3(PB)となり、
内項と外項の積から、PQ=√3となる。
(4)① 84.3%
n多角形の内角の和→180(n-2)
180×(5-2)=540°
五角形はよくでてくるので、覚えてしまった方が早い。(六角形は720°)
② 64.1%
なんとなくでも解けてしまうが、論理的に説明できるようにしよう。
△ABCと△ABEに注目。
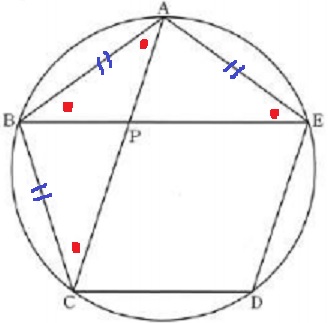
2辺とあいだの角が等しい、合同な二等辺三角形。
∠ABP=∠BAP(●)=(180-108)÷2=36°
△ABPで外角定理→∠BPC=36+36=72°
③ 1.3%!!
角度を調べていくと、△AEPは底角が等しくなり、二等辺三角形。
AC(正五角形の対角線)をxとおく。

正五角形の1辺は2cm。AE=PE=2cm
BP=x-2cm
△ABEと△PBAはともに二等辺で2角が等しく∽
AB:BE=PB:BA
2:x=(x-2x):2
x(x-2)=4
x2-2x-4=0
解の公式を適用。b’=2bバージョンが使える。
x>0より、x=1+√5
AC=1+√5cm
@黄金比@
正五角形の一辺を1としたとき、対角線の長さは(1+√5)/2となる。
1:(1+√5)/2は、幾何的に美しい比率とされる黄金比。
今年の島根県でも出題されました。
難しいですが、ラストの問題にでてくる図形を利用すると、
コンパスと定規で正五角形が作れます。
大問4(関数)
(1) 82.4%
A(-2、2)をy=ax2に代入。
2=(-2)2a
a=1/2
(2) 46.9%
B座標を求める。
y=1/2×12=1/2
B(1、1/2)
A(-2、2)⇒B(1、1/2)
右に3、下に-3/2なので、傾きは-3/2÷3=-1/2
Aから右に2移動すると、下に1下がるので、切片は1となる。
y=-1/2x+1
(3)① 26.3%!
線分AC上の点でx座標が整数となる点は7個
⇒Aのx座標が-2なので-2+7=5としたいところだが、0を含むことに注意!
〔-2・-1・0・1・2・3・4〕
Cのx座標は4
y=1/2x2に代入。
C(4、8)
② 1.3%!!
Cの座標から、OC:y=2x
PはOCと、ℓ:y=-1/2x+1の交点座標。
2x=-1/2x+1
x=2/5、y=4/5
P(2/5、4/5)

△AOP:△PBCの面積比は、AP×OP:CP×BPをすればいい。
各々の点座標から距離の比を算出。
AP:PB=12/5:3/5=4:1
OP:PB=4/5:36/5=1:9
△AOP:△PBC=(4×1):(1×9)=4:9
大問5(空間図形)
(1) 76.3%
△OPQで三平方。
OP=√(92-32)=6√2cm
(2) 30.6%!
アイス型の表面積を求める。
円錐の側面積となる扇形の中心角は、〔×半径/母線〕で処理をする。
球の表面積は、S=4πr2。半球は半分にすればいい。
9×9×π×3/9+4π×32×1/2
=45πcm2
(3) 17.5%!
OP=6√2
体積比は相似比の3乗なので、
円錐の体積:水の体積=6√23:63=63×√23:63
=√23:1
=2√2:1
円柱の体積から水の体積を求める。
3×3×π×6√2×1/3×1/2√2=9πcm3
球の体積は4/3πr3
半球の体積は、4/3π×33×1/2=18πcm3
9π/18π=1/2=50%
(4) 0.2%!!!
円錐の先を円柱の隅っこに差し込む。
求める長さは円柱の底面積である円の円周にあたる。
円周を計算するには、円の直径がわかればいい。
そこで、立体を横からみる。
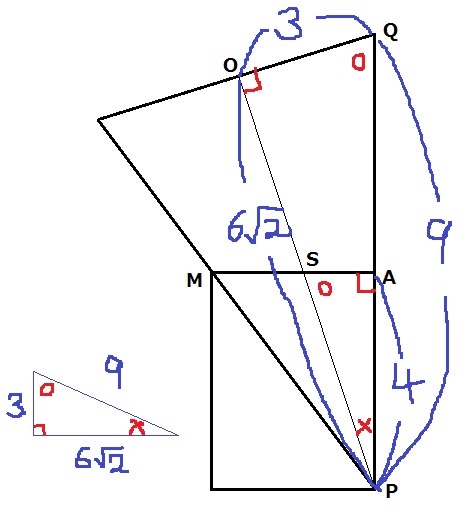
MAが円の直径にあたる。
相似を使うと予想して、角度を調べる。
○+×=90°を利用すると2角が等しく、△OPQ∽△APS
△OPQの辺の比は、3:9:6√2=1:3:2√2
本問で、角度が○-×-90°の直角三角形は辺の比が1:3:2√2になる。
SA=4×1/2√2=√2
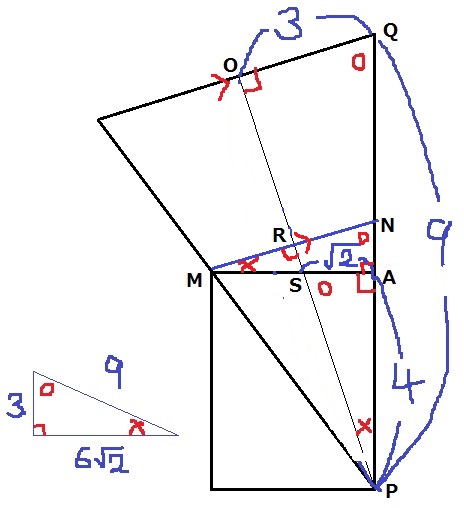
Mを通る円錐の底面に平行な線をひき、交点をR、Nとする。
平行より同位角から∠MNA=∠OPN=○
長方形の外角から∠NAM=90°なので、残りの∠NMA=×
MN⊥OPより、∠MRS=90°
2角が等しいので、△SRM∽△NAM

↑拡大。SM=xとおく。
角度が○-×-90°なので、辺の比が1:3:2√2
RM=2√2/3x
NM=RM×2=4√2/3x
△NAMより、MA=4√2/3x×2√2/3=16/9x
ということは、16/9x-x=7/9x=√2
x=9√2/7
MA=9√2/7+√2=16/7√2
ADは、これを直径とする円周なので16√2/7πcm




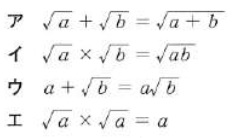

コメント