2021年度　山形県公立高校入試問題過去問【数学】解説

合格者平均49.5点（前年比；－3.5点）
問題はコチラ→ＰＤＦファイル
出題範囲の除外は標本調査。

大問１（小問集合）

（１）①　95.8％
２－（３－８）
＝２＋５＝７

②　83.2％
（１/３－３/４）÷５/６
＝－５/12÷５/６
＝－１/２

③　75.6％
（－４ｘ）²÷12ｘｙ×９ｘｙ²
＝16ｘ²÷12ｘｙ×９ｘｙ²
＝12ｘ²ｙ

④　88.5％
√18－10/√２
＝３√２－５√２
＝－２√２

（２）　82.8％
答案では求め方も記述する。
（ｘ－４）（３ｘ＋２）＝－８ｘ－５
３ｘ²－10ｘ－８＝－８ｘ－５
３ｘ²－２ｘ－３＝０

解の公式を適用。ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝（１±√10）/３

（３）　57.6％
△ＡＢＣの内角は30°－60°－90°⇒辺の比は１：２：√３。
ＡＣ＝３ｃｍ、ＢＣ＝３√３ｃｍ
３×３√３÷２×４＝18√３ｃｍ³

（４）　66.0％
Ａ：２を取る。３個から１個を選ぶので、確率は１/３。
Ｂ：５は取らない。同様に考えて１/３。
Ｃ：４個から２個を選ぶ⇒₄Ｃ₂＝６通り
　和が偶数となるのは（７・９）（８・10）の２通り。
　確率は２/６＝１/３
したがって、どれも確率は同じ。エ

（５）　18.3％！
ア

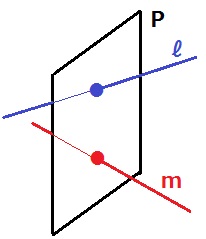
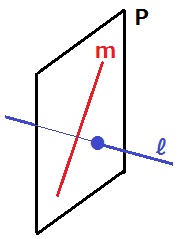
平面Ｐと交わる２直線が交わるとは限らない。

イ

平面Ｐに平行な２直線が平行とは限らない。

ウ

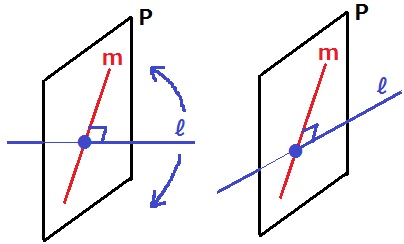
わかりづらくて申し訳ない(´～`)
左図は直線ℓ⊥平面Ｐだが、直線ℓ⊥直線ｍを維持したままℓを傾けることができる。

エ
 
絶対ネジレになる。答えはエ。

大問２（小問集合２）

（１）①　67.9％
ｘ＝０のとき、最大値０
ｘ＝４のとき、最小値－８
－８≦ｙ≦０

②　43.9％

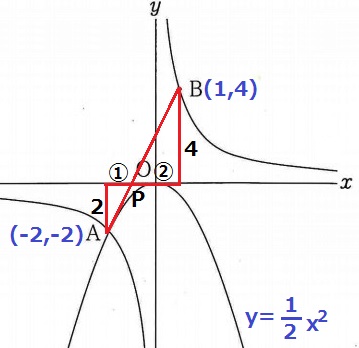
ｙ＝－１/２ｘ²にｘ＝－２を代入。Ａ（－２、－２）
反比例の式はｙ＝４/ｘ。Ｂ（１、４）

上のような三角形の相似をつくる。
ｙ座標より辺の比は①：②。
ＡとＢのｘ座標の差は３だから、Ｐのｘ座標は－２＋３×①/③＝－１

（２）　53.4％

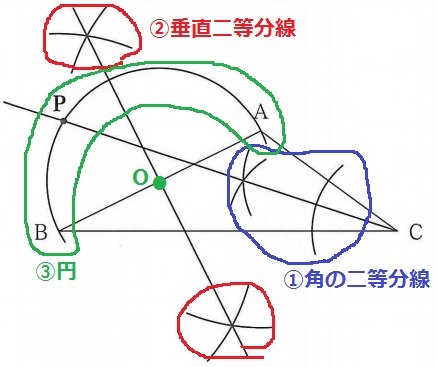
『ＡＣとＢＣから等距離』⇒∠ＡＣＢの二等分線
Ｐは外部にあるので、∠ＡＰＢ＝90°は円周角定理が作りやすい。
半円の弧に対する円周角は90°。直径をＡＢとする円の円周上にＰがある。
①∠ＡＣＢの二等分線
②ＡＢの垂直二等分線。Ｏが円の中心である。
③円を作図。①と円周の交点がＰ。

（３）①　50.0％
大きい袋をｘ個、小さい袋をｙ個とする。
袋の数で等式。
ｘ＋ｙ＝50

もう１つは里芋の数で等式。
『大１つに８個、小１つに５個入れると67個残る』
→８ｘ＋５ｙ＋67
『大１つに10個、小１つに６個入れると、小２つだけ５個になる』
→大の合計は10ｘ個。小の合計は６ｘ個に２個分だけ少ない。

ｘ＋ｙ＝50
８ｘ＋５ｙ＋67＝10ｘ＋６ｙ－２

②　19.8％！
先の連立を説く。
ｘ＋ｙ＝50　…①
後半の式を簡単にすると、
２ｘ＋ｙ＝69　…②

②－①でｘ＝19
①に代入してｙ＝31
里芋の個数は、
10ｘ＋６ｙ－２
＝10×19＋６×31－２
＝374個

（４）100％…26.3％！、50～99％…29.0％、１～49％…14.5％
さくらんぼの種飛ばし大会・・(･Д･)

代表値を比較すればいい。階級値で示すこと！
最頻値（モード）は知也が6.5ｍ、公太が5.5ｍで知也の方が大きい。
*ちなみに、20回の中央値（メジアン）は10番目と11番目の平均でともに5.5ｍ。

大問３（数量変化）

（１）①　83.6％
グラフより、ｙ＝４のときｘ＝８
午前10時８分

②ア…70.6％、イ…55.3％、ウ…43.5％、図…85.1％

グラフから考える。
10：12に公園到着→公園は駅から６ｋｍ地点にある。
10：18に出発だから、公園には６分間滞在した。
公園から空港までの距離は、18－６＝12ｋｍ
時速40ｋｍで走るので、12÷40＝0.3時間＝18分
空港に到着した時刻は、10：18＋18＝10：36
グラフは（18、６）（36、18）を通過する。

■０≦ｘ≦12
右に２進むと上に１あがるから傾きは１/２。
原点を通るので、ｙ＝１/２ｘ
■12≦ｘ≦18
ｙ＝６
■18≦ｘ≦36
右に３進むと上に２あがるから傾きは２/３。
ｙ＝２/３ｘ＋ｂに（ｘ、ｙ）＝（18、６）を代入。
６＝２/３×18＋ｂ
ｂ＝－６
ｙ＝２/３ｘ－６
ア…ｙ＝１/２ｘ、イ…36、ウ…ｙ＝２/３ｘ－６

＠余談＠

格子点を追っていけば切片を求められる。

（２）エ…53.1％、オ…8.8％！

公園の横線（ｙ＝６）に交わるように線を描く。
バスが横線に接する（18、６）を通る直線より傾きは大きい。
12分間で６ｋｍ走るから、６×60/12＝時速30ｋｍ

また、空港到着前にバスは自動車に追い越されるので、
（36、18）を通る直線よりも傾きは小さい。
30分間で18ｋｍ走るから、18×60/30＝時速36ｋｍ
バスの速さは時速30ｋｍより速く、時速36ｋｍより遅い。
エ…30、オ…36

大問４（平面図形）

（１）　63.7％

ＤＥ//ＡＢの錯角で∠ＧＢＯ＝40°
これは弧ＡＣの円周角に相当するので、∠ＡＯＣはその中心角だから、
40×２＝80°

（２）100％…1.5％!!、50～99％…3.4％、１～49％…71.4％
△ＯＣＨ≡△ＯＥＦの証明。

共通角の∠ＣＯＨ＝∠ＥＯＦ
半径よりＯＣ＝ＯＥ
問題はもう片方の角度・・。

ポイントはＯＤ//ＢＧ、ＤＧ//ＯＢより、
四角形ＯＢＧＤは２組の対辺が平行⇒平行四辺形であること！
また、円の半径から△ＯＣＢと△ＯＤＥがともに二等辺三角形。
①二等辺ＯＣＢの底角⇒②平行四辺形ＯＢＧＤの対角⇒③二等辺ＯＤＥの底角。
１辺両端角が等しく合同。

（３）　0.4％!!!
△ＣＦＧが求めにくい位置にある。

なんとなく△ＣＦＧと△ＥＨＧが合同っぽい。。
先ほどの△ＯＣＨ≡△ＯＥＦを手がかりにすると、一辺両端角相等で△ＣＦＧ≡△ＥＨＧ。
（半直線ＯＧを対称の軸に図形が左右対称である）

つまり、△ＥＨＧを求積すればいい。

平行四辺形の対辺からＤＧ＝４ｃｍ
ＧＥ＝６－４＝２ｃｍ
△ＨＧＥ∽△ＨＢＯより、ＥＨ：ＨＯ＝①：②

△ＥＨＧにおいて底辺をＧＥとしたときの高さが知りたい。

有名角が見当たらないので、高さは三平方を用いる。
二等辺三角形ＯＤＥでＯから垂線をひくと、足のＩはＤＥの中点である。
△ＯＩＥで三平方→ＩＯ＝√７ｃｍ
ＨからＧＥに垂線、足をＪとする。
△ＪＥＨ∽△ＩＥＯより、ＪＨ＝√７×①/③＝√７/３ｃｍ
△ＥＨＧの面積は、２×√７/３÷２＝√７/３ｃｍ²