平均26.8点(前年比;+3.9点)
最高点48点、最低点0点
問題はこちら→リセマムさん
大問1(計算)
(1)
3×(-5)+9
=-15+9
=-6
(2)
5(x-2y)-(4x+y)
=5x-10y-4y-y
=x-11y
(3)
(6a2-4ab)÷2a ←分配法則
=6a2÷2a-4ab÷2a
=3a-2b
(4)
(√8+1)(√2-1)
=4-2√2+√2-1
=3-√2
(5)
3x2-12
=3(x2-4)
=3(x+2)(x-2)
(6)
(x-2)2=5
x-2=±√5
x=2±√5
(7)
nだけだとnは偶数か奇数か決まらないが、2nは2で割り切れるから必ず偶数。
偶数+奇数=奇数なので2n+1は奇数。これと連続する奇数は2n+3(or2n-1)
エ
大問2(図形)
(1)
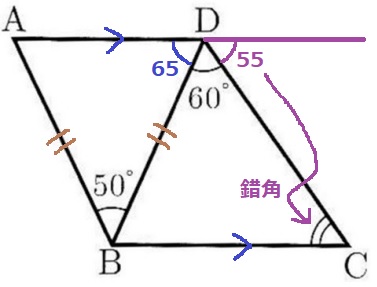
△ABDは二等辺三角形。
∠ADB=(180-50)÷2=65°
右の角は、180-(65+50)=55°
AD//BCの錯角で降ろして、∠BCD=55°
(2)ア

長方形の対辺であるBC//EDに着目するとわかりやすい。
BCは△ABCの1辺で面ABCに含まれる辺だから、面ABCとDEは平行。イ
イ
△BCEで三平方→EC=4√5cm
Aから垂線をおろし、底面との交点をHとする。
四角錐の高さAH=30×2÷4√5=3√5cm
四角錐の体積は、8×4×3√5÷3=32√5cm3
(3)
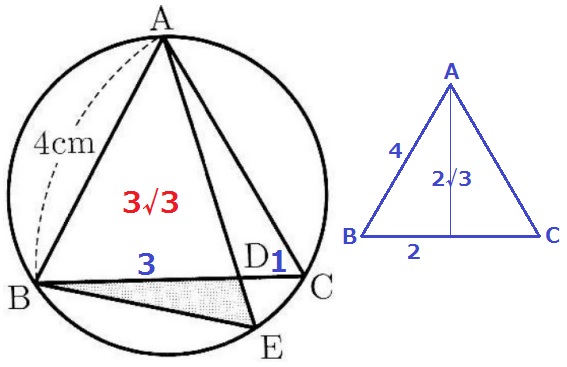
面積が求めやすいのは正三角形ABC。
1辺4cm、半分に割ると1:2:√3の直角三角形で高さは2√3cm。
BD:DC=3:1から、△ABD=4×2√3÷2×3/4=3√3cm2
AD:DEがわかれば、△BDEが求まる。

CEに補助線。
円周角や対頂角から2角相等で△ABD∽△CED
CE:ED=AB:BD=④:③
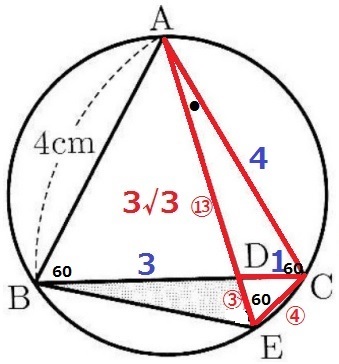
弧ACに対する円周角より、∠AEC=60°
共通角●と60°で2角相等で→△ACD∽△AEC
AE:EC=AC:CD=4:1
AE=④×4=⑯
AD=⑯-③=⑬
△BDEの面積は、3√3×③/⑬=9√3/13cm2
大問3(小問集合)
(1)
全体は、6×6=36通り
aは十の位、bは一の位。
位の数が1~6である2桁の8の倍数を調べる。
⇒16、24、32、56、64の5通り
確率は5/36
(2)
6ヶ月の平均値…(1+6+4+2+8+3)÷6=24÷6=4冊
7ヶ月の平均値…(24+4)÷7=4冊
平均値は変わらない。
6ヶ月の中央値…3番目と4番目の平均で3.5冊。
7ヶ月の中央値…4番目の4冊。
中央値は大きくなる。
イ・エ
(3)ア
y=ax2において、xの値がp→qに増加するときの変化の割合はa(p+q)
1/4(-1-3)=-1
イ
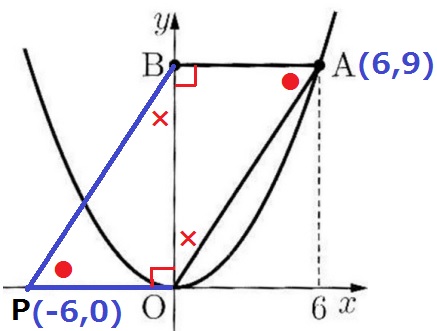
なんとなく四角形ABPOが平行四辺形っぽい。
△ABOと△POBにおいて、共通辺はOB、仮定の●と90°が等しい。
残りの角の×が同じから1辺と両端角が等しく、△ABO≡△POB
PO=AB=6なので、P(-6、0)
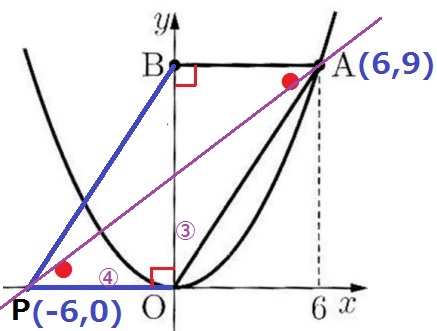
P(-6、0)⇒A(6、9)
右に12、上に9だから、傾きは9/12=3/4
切片はPから右に④、上に③移動するので、6×③/④=9/2
y=3/4x+9/2
(4)
答案では求める過程も書く。
箱Aがa枚、箱Bがb枚、箱Cが2a枚。
a+b+2a=3a+b=27 …①
8a+4b+3a×2=14a+4b=118 …②
②-①×4をして、2a=10
a=5
これを①に代入して、b=12
a…5、b…12
大問4(規則・数量変化)
(1)ア
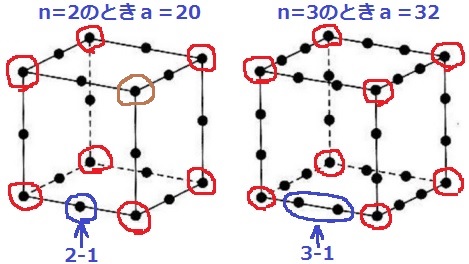
頂点とそれ以外に分けて数える。
立方体の頂点は8個。
●n=2
頂点以外の点は1辺あたり2-1=1個
立方体は12辺あるから、a=8+1×12=20
●n=3
頂点以外は1辺あたり3-1=2個
a=8+2×12=32
n=5のときは、a=8+(5-1)×12=56
イ
先の法則をnで示すと、a=8+12(n-1)=12n-4

問題はb
●n=2
正四面体の頂点は4個。
頂点以外の点は1辺あたり2-1=1個
正四面体は6辺だから、b=4+(2-1)×6=10
nが偶数の場合、aと同様に1辺あたりn-1個である。
●n=3
頂点以外の点は1個あたり3個。
b=4+3×6=22個
nが奇数の場合、中点が追加されるので1辺あたりn個である。
【nが偶数の場合】
b=4+6(n-1)=6n-2
a-b
=(12n-4)-(6n-2)
=6n-2=70
n=12(偶数なので条件適合)
【nが奇数の場合】
b=6n+4
a-b
=(12n-4)-(6n+4)
=6n-8=70
n=13(奇数なので条件適合)
n=12、13
(2)ア
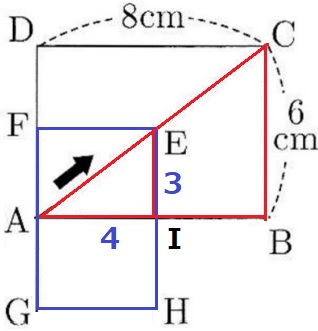
↑FがDA上にきたときの様子。
ABとEHの交点をHとする。
△EAI∽△CABより、AI:EI=AB:CB=4:3
AI=4cmだから、EI=3cm
重なる部分の図形Sの面積は、4×3=12cm2
(*△EAIは3:4:5の直角三角形で、このときのAEは5cm)
イ
Eの速さは毎秒1cm。
5秒後はAE=5cmで、Fが辺DAと重なる。
10秒後はAE=10cmで、EがCと重なる。
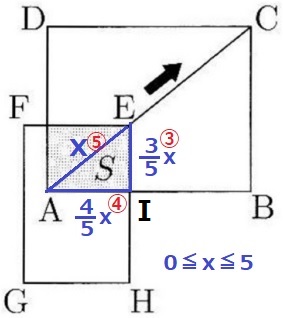
0≦x≦5のとき、横AIと縦EIがともに伸びるので、
図形Sの面積はy=ax2で増加する。
△EAIの辺の比は③:④:⑤でAE=xより、
AI=4/5x、EI=3/5x
Sの面積は、4/5x×3/5x=12/25x2cm2

5≦x≦10のとき、横は4cmで固定。
縦EIだけが伸びるからSの面積は一次関数で増加する。
S=4×3/5x=12/5xm2
0≦x≦5のとき…12/25x2cm2、5≦x≦10のとき…12/5xcm2
ウ
答案では求める過程も書く。
t秒後のSの面積を5倍すると、t+6秒後の面積に相当する。
xの最大値は10なので、t+6≦10→t≦4
また、t=0のときSの面積は0cm2で、6秒後は0cm2ではないから×
→tの範囲は0<t≦4
前問の解答を活用する。
t秒後のSの面積…4秒以下だから、12/25x2のxにtを代入して12/25t2
t+6秒後のSの面積…6秒より大きいから、12/5xのxにt+6を代入して12/5(t+6)
12/25t2×5=12/5(t+6)
12/5t2-12/5t-72/5=0 ←×5
12t2-12t-72=0 ←÷12
t2-t-6
=(t-3)(t+2)=0
0<t≦4より、t=3
大問5(図形の証明)
(1)
△ACD∽△AEBの証明。
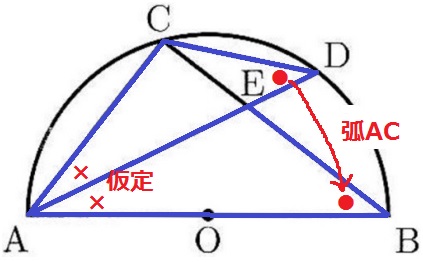
仮定(×)と弧ACに対する円周角(●)→2角相等で∽
(2)
△OFG≡△OHGの証明。

問題文にしたがってF・G・Hを追記。
∠OFG=90°なので、これに対応する∠OHG=90°を導きたい。
他に90°がないか探すと、半円の弧に対する円周角である∠ACB=90°
∠ACBと∠OHGは同位角の関係にあたる。
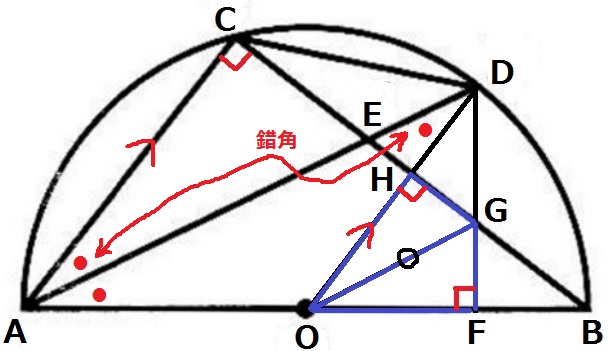
半径でOA=OD、△AODは二等辺三角形で∠ODA=●
∠CAD=∠ODA(●)で錯角が等しいゆえ、AC//OD
2直線が平行だから、同位角で∠ACB=∠OHG=90°
△OFGと△OHGは直角三角形で、斜辺OGで共通。
直角三角形の合同条件で他の辺か一鋭角が使えないか検討する。
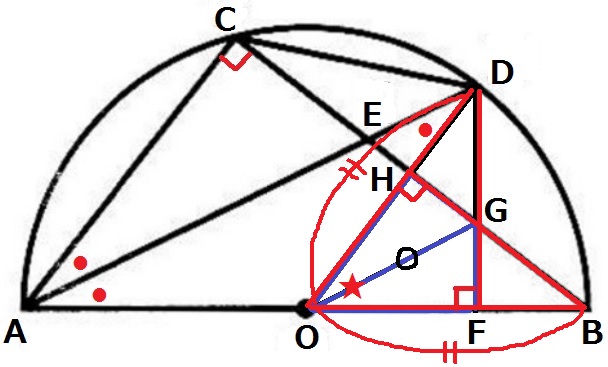
直接指摘できない場合は、他の三角形の合同を経由する。
∠DFO=∠BHO=90°、半径でOD=OB、共通角★から、
斜辺と1鋭角が等しい直角三角形なので△DOF≡△BOH
対応する辺から、OF=OH
斜辺と他の1辺が等しい直角三角形だから、△OFG≡△OHG
●講評●
大問1
全部とりたい。
(6)カッコは展開しない。
(7)n単独では決まらない。2nは偶数。
その両隣の2n-1、2n+1は奇数。奇数+偶数=奇数
大問2
(3)例年、一筋縄ではいかない図形問題がでてくる。
手ごわいので後回しでもOK。解説では問題集にでてくる相似形をつくった。
大問3
(3)イ:△ABOを点対称移動して平行四辺形をつくるイメージ。
(4)文字数はあるが、箱Cが2aとわかれば基本問題。
大問4
ここも厳しいか。
(1)いろんな考え方があると思う。
頂点とそれ以外に分けて、それ以外は1辺あたりの数で算出した。
1辺あたり個数とnの関係はn-1である。
正四面体はnが偶数か奇数かで処理が異なる。
(2)もはや独立した大問。
イ:縦と横の長さをxで表す。5秒以降は横=4cmで計算。
ウ:tの範囲を確定しよう。
面積を5倍に拡大するには、y=ax2の増加を頼らないと厳しい。
tは最低でも5秒以下であるとわかる。
大問5
(2)部分点狙いで何か書きたい。
90°を別の角度から指摘する。AC//ODであれば嬉しい→等しい錯角か同位角を探す。
もう1つが難しい。GF=GHや角度は難しそう。
OF=OHを1辺とする三角形の合同で攻める。このとき、先ほど指摘した90°を用いる。



コメント