2018年度　京都府公立高校入試前期【数学】解説

大問３からレベルが上がり、最後の規則は複雑です。
問題はコチラから→リセマムさん
京都府教育庁指導部にもありました。
2019年度解説はコチラ⇒前期　中期

大問１（小問集合）

（１）－２²－８÷（－５）
＝－４＋８/５＝－１２/５

（２）４ａ²ｂ÷（－２/５ａｂ）×7ｂ²
＝－７０ａｂ²

（３）（２ｘ－１）²－（ｘ＋３）（ｘ－６）
＝４ｘ^２－４ｘ＋１－（ｘ²－３ｘ－１８）
＝３ｘ²－ｘ＋１９

（４）ｎ角形の内角の和→１８０（ｎ－２）を使う。
１８０（３０－２）÷３０＝１６８°

（５）連立方程式
代入法でも加減法でも。
ｘ＝５、ｙ＝－４

（６）いきなり代入するのではなく、式を整理する。
ｘ²ｙ－2ｘｙ＝ｘｙ（ｘ－２）
＝（√６＋２）（√６－２）（√６＋２－２）＝（６－４）・√６＝２√６

（７）（３ｘ－５）（ｘ＋１）＝０

（８）（ｙの増加量）/（ｘの増加量）＝傾き
（ｙの増加量）/６＝４/３　　ｙの増加量＝８

（９）なかなか面白い出し方です。
Ｘをつかって、平均値＝中央値となる一次方程式を立てる。
中央値は、５とＸの平均になる。
（２＋２＋５＋Ｘ＋１３＋１５）/６＝（５＋Ｘ）/２
３７＋Ｘ＝３（５＋Ｘ）
２Ｘ＝２２
Ｘ＝１１

大問２（関数）

（１）
Ａ（－３、１２）をｙ＝ａx²に代入する。
１２＝９ａ　　ａ＝３/４

（２）
Ｂ（３、１２）　Ｃ（０、２４）
傾きは右に３で下に１２だから、－４
よって、ｙ＝－４ｘ＋２４

（３）
ひし形全体の面積が、６×２４×１/２＝７２ｃｍ²
△ＡＢＣはその半分なので３６ｃｍ²
△ＡＤＣが１２ｃｍ²なので、△ＡＢＣの面積の３分の１である。
ＢＣを底辺にみると、ＢＤ：ＤＣ＝２：１にする。
よって、Ｄ（１、２０）

大問３（確率）

（１）
袋Ａで１がでたら、袋Ｂで〔１・２〕以外を出す確率は４/５
袋Ａで２がでたら、袋Ｂで〔１・２〕以外を出す確率も４/５
袋Ａで３がでたら、袋Ｂで〔３・４〕以外を出す確率も４/５・・・
袋Ａで４～８をだしても同様。よって、４/５

（２）
袋Ａの数字で場合分け。
袋Ａで８を出す。袋Ｂで何をだしても積は８の倍数となる。→５通り
袋Ａで４を出す。〔２の倍数×４の倍数＝８の倍数〕なので、袋Ｂで偶数を出せばよい→５通り
袋Ａで２を出す。４の倍数をもつ〔３・４〕〔７・８〕→２通り
偶数である６も、２と同様。→２通り
他の奇数（１、３、５、７）は〔７・８〕のみ→各１通りで計４通り
袋Ａと袋Ｂの取り出し方は、８×５＝４０通りなので、
（５＋５＋２＋２＋４）/４０＝１８/４０＝９/２０

大問４（平面図形）

（１）
△ＤＣＭ∽△ＣＡＭの証明。
ＡＣに補助線。
問題文から∠ＣＤＭ＝９０°
円周角定理から、直径ＡＭに対する円周角∠ＡＣＭ＝９０°
∠ＣＭＤが共通角。　２角が等しいので相似。

（２）
ＡＦに補助線。
直径ＡＭに対する円周角から、∠ＡＦＭ＝９０°
問題文から∠ＥＤＭ＝９０°
△ＦＭＡと△ＤＭＥにおいて、∠ＥＭＤが共通角だから、
残りの角も、∠ＦＡＭ＝∠ＤＥＭとなる。
半径から、ＡＭ＝ＥＭ＝４ｃｍ
１辺と両端角から、△ＦＭＡ≡△ＤＥＭとなる。

上の合同から、ＦＭ＝ＤＭ
（１）の相似を利用。
ＡＭ：ＣＭ＝ＣＭ：ＤＭ＝４：３　ＤＭ＝３×３/４＝９/４ｃｍ
したがって、ＦＭ＝９/４ｃｍ

（３）
ＥＭを右下にのばし、円周との交点をＧとおく。
２つの直径に挟まれる２つの三角形は合同。△ＭＧＢ≡△ＭＥＡ
つまり、△ＭＥＡの面積を調べればよい。
高さＥＤは、△ＥＤＭで三平方。
ＥＤ＝√(１６² －（9/4）² )＝５/４・√７
△ＥＤＭ＝４×５/４・√７×１/２＝５/２・√７ｃｍ²

大問５（空間図形）

（１）
△ＡＢＣは、１：１：√２の直角三角形→ＡＣ＝６√２
その半分で、ＡＨ＝３√２ｃｍ

正四角錘の高さＯＨは、△ＯＡＨで三平方。
ＯＨ＝√{（６√３）²－（３√２）^２}＝√（１０８－１８）＝√９０＝３√１０ｃｍ
よって、体積は、６×６×３√１０×１/３＝３６√１０ｃｍ₃

（２）
方針：Ｏ－ＡＢＣＤ（正四角錘全体）→Ｏ－ＡＢＤ→Ｂ―ＯＰＱ
Ｏ－ＡＢＤは、正四角錘の半分。
Ｏ－ＡＢＤ：Ｂ－ＯＰＱ＝△ＯＡＤ：△ＯＰＱ
（底面を△ＯＡＤとすれば、高さが同じだから）
ＰとＱは中点なので、辺の比→面積比から、△ＯＡＤ：ＯＰＱ＝４：１
以上から、３６√１０×１/２×１/４＝９/２・√１０ｃｍ₃

（３）
△ＯＡＢを正面にして、平面で考えよう。
点Ｅを作図し、ＰＨに補助線。

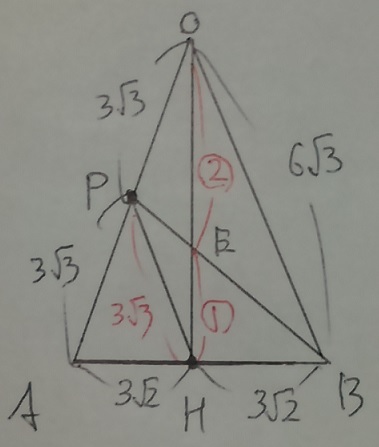
点Ｐと点Ｈはともに中点。
△ＡＢＯで中点連結定理が使える（ＯＢを底辺としてみるとわかりやすい）
ＰＨ//ＯＢ、ＰＨ：ＯＢ＝１：２
△ＥＰＨ∽△ＥＢＯとなり、辺の比は１：２
ＯＥ：ＥＨ＝２：１
（１）より、ＯＨは３√１０だから、３√１０×２/３＝２√１０ｃｍ

大問６（規則）

（１）
１～２３の玉を３コずつ入れていく。
２３÷３＝７・・２
→８箱目の２つ目に２３の玉が入り、余りの１つに次の１の玉が入る（表でも確認）。
８箱目の玉は〔２２・２３・１〕。２３個いれるたびに、余りの１で１コずつズレる。
つぎの２３の玉がはいるときは、１コズレて、〔２３・１・２〕となる。
よって、求める解は２回目の２３の玉をいれるとき。
もっというと、はじめの１の玉から、２３×２＝４６個目の玉をいれたとき。
玉は１箱３つずつなので、４６÷３＝１５・・1　→１６箱目
箱の種類はＡ～Ｄの４種類。１６÷４＝４　→余りなしなのでＤ

（２）
８回目の１の玉→１～２３を７周＋８回目の１＝２３×７＋１＝１６２個目
前問と同様。
１６２÷３＝５４　→５４箱目
５４÷４＝１３・・２　→余り２からＢ

（３）
１の玉を聞かれているので、１の玉が何箱目にくるかを考える。
１の玉は２３ずつ足していって、
１個目、２４個目、４７個目、７０個目、９３、１１６、１３９、１６２、１８５、２０７、２３０・・
１箱に３コずつだから、上の数字を÷３し、あまりがでたら商に＋１をする。すると、、
１箱目、８箱目、１６箱目、２４、３１、３９、４７、５４、６２、７０、７７箱目・・に１の玉がくる。
（基本的に＋８で、３回ごとに＋７）
○箱目÷４の余りで箱の種類が確定するので、１の玉が入る箱は、
Ａ、Ｄ、Ｄ、Ｄ、Ｃ、Ｃ、Ｃ、Ｂ、Ｂ、Ｂ、Ａ・・・
（１）でやったように、余りの１で玉が１個ずつズレるので、３個ズレると手前の箱に収まる。
（Ａ・Ｄ×３・Ｃ×３・Ｂ×３）と計１０周の【１～２３】がきて、次に１の玉が箱Ａに入る。答えは、２３０個目の１で、７７箱目。

式であらわすと、
２３×（１＋３×３）＋１＝２３０個目
２３０÷３＝７６・・２　　→７７箱目

＠＠

３０回目にＡの箱に入る１を求める。
ここは捨てて良いと思います（笑）

１の玉が入る箱の種類は、
Ａ/ＤＤＤ・ＣＣＣ・ＢＢＢ・ＡＡＡ/ＤＤＤ・ＣＣＣ・ＢＢＢ・ＡＡＡ/ＤＤ・・・と続く。
３０回目のＡがくる箱の順番が答え。

ＤＤＤ・ＣＣＣ・ＢＢＢ・ＡＡＡで区切りたいところですが、サボのおすすめは【ＡＤＤＤＣＣＣＢＢＢＡＡ～（次のＡの手前まで）】。
１の玉がＡに入る１回目は１箱目、〔１、２、３〕
２回目は前の問題より７７箱目、〔２２、２３、１〕
次は＋８して、８５箱目、〔２３、１、２〕
次は＋８して、９３箱目、〔１、２、３〕
となると、９２箱目がちょうど〔２１、２２、２３〕と区切り良く終わるので、９３箱目を新しい周期のはじまりとすれば、１箱目の〔１、２、３〕と同じ規則でスタートし、２３コの玉をかたまりとして倍にしやすいからです。

１周期をＡＤＤＤＣＣＣＢＢＢＡＡ～（次のＡの手前）とし、９２箱分とする。
３０÷３＝９周期・・２
１周期が９２箱分で、最後の余り２は〔ＡＤＤＤＣＣＣＢＢＢＡ〕の８５箱分。
９２×９＋８５＝９１３箱目

最後は他に良い方法があるかも（汗）見つけた方はお問い合わせにて教えてくださいませm(_ _ )m
公立高校入試解説ページに戻る