平均59.0点(前年比;-10.8点)
問題はこちら→リセマムさん
大問1(小問集合)
(1)ア
3-2×32
=3-18
=-15
イ
√12-6/√3
=2√3-2√3
=0
ウ
6ab÷3a×2b
=4b2
(2)
(2x+1)(x+2)=2x+3
2x2+5x+2=2x+3
2x2+3x-1=0
解の公式を適用して、x=(-3±√17)/4
(3)
標本の抽出が3年生だけなので、1年生と2年生の傾向が調査結果にあらわれないため。
*標本は属性の偏りなく、無作為に抽出する。
ちゃんとした世論調査では日本の性別や年齢別の割合に応じた人口構成比をもとに抽出する。
(4)
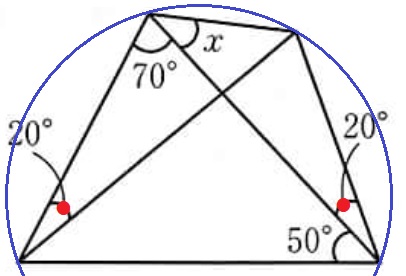
20°に注目すると、円周角定理の逆で四角形の4つの頂点が同一円周上にくる。
円に内接する四角形の対角の和は180°だから、
70+x+50+20=180
x=40°
(5)
2けたの整数の十の位をxとする。
(10x+3)2
=100x2+60x+9
=10(10x2+6x)+9
10x2+6xは整数だから、(10x+3)2を10で割ると余りが9となる。
(6)
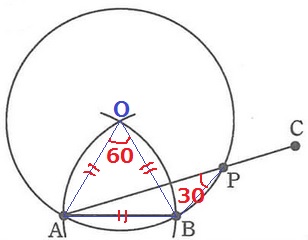
30°の作図は60°を半分にする。
線分ACが傾いているので、角の二等分線ではなく円周角の定理を想起しよう。
①ABの長さをとり、正三角形OABを作成。
②Oを中心にグルっと円を描く。
中心角AOBの円周角APBは60÷2=30°
円とACとの交点がPとなる。
大問2(確率)
(1)
1回目に”何か”を出す。
2回目に、その”何か”がまた出るのは1/5。
(2)

たとえば、Bを引いた場合、C・D・Eでないと三角形がつくれない→3通り
Bと対称的な位置にあるCも同様→3通り
Fを引いた場合も3通り。対称性でEも同様で3通り。
Dだけ4通りある。
3×2+3×2+4=16通り
全体は5×5=25通りなので、確率は16/25。
@別解@
余事象でもいける。
三角形をつくれない場合は、同じ文字をつづけて引いた場合→5通り
また、直線になってしまう(B、F)(C、E)、これらの逆を合わせて4通り
計9通り
三角形がつくれる場合は、25-9=16通りとなる。
大問3(方程式)
(1)
小学生をx人とすると中高生は2x人で、和は3x人。
大人はy人。
合計して、3x+y人
(2)ア
連立をつくる。
1つは人数で等式。
『大人は小中高生より100人少なかった』ので、大人y人は3x-100人。
y=3x-100
もう1つは金額で等式。
入館料は小学生…260x円、中高校生…410×2x円、大人…760y円
お土産は(3x+y)×0.8人が購入したから、お土産代は550×(3x+y)×0.8円
これらを合計して、260x+410×2x+760y+550×(3x+y)×0.8=150000
y=3x-100
260x+410×2x+760y+550×(3x+y)×0.8=150000
イ
うえの連立を解く。
y=3x-100…①
260x+820x+760y+1320x+440y=150000
2400x+1200y=150000 ←÷600
4x+2y=250…②
①を②に代入。
4x+2(3x-100)=250
10x=450
x=45
①に代入。
y=3×45-100=35
x=45、y=35
大問4(平面図形)
(1)
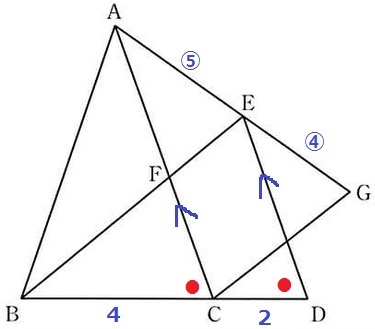
二等辺ABCを縦に分割。
高さを三平方で算出すると4√2cm
△ABCの面積は、4×4√2÷2=8√2cm2
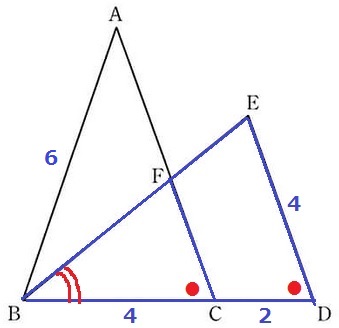
合同より、BC=DE=4cm
CD=6-4=2cm
対応する角で∠BCF=∠BDE(●)
共通角とあわせると2角が等しく、△BCF∽△BDE
CF=4×4/6=8/3cm
(2)ア
△AFE∽△ACGの証明。
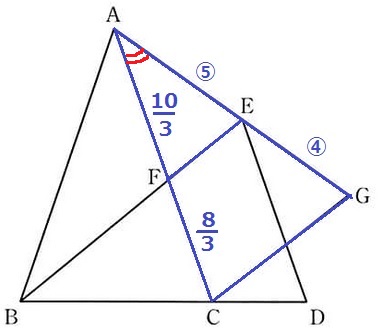
仮定より、AE:EG=5:4
先ほどCF=8/3cmとだしたので、試しにAFを計算してみると、
AF=6-8/3=10/3cm
AF:FC=10/3:8/3=5:4
共通角と合わせると、2辺の比とあいだが等しいので∽
イ
(1)の証明で●に注目すると、同位角が等しいからAC//ED
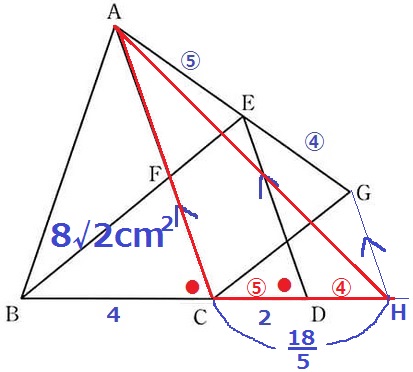
Gを通るACに平行な線をひき、BCの延長線との交点をHとする。
等積変形で△ACHを求積すればいい。
平行線と線分の比より、AE:EG=CD:DH=⑤:④
CH=2×⑨/⑤=18/5cm
△ABCは8√2cm2と求めている。
△ABC:△ACH=BC:CH=4:18/5=10:9
したがって、8√2×9/10=36√2/5cm2
大問5(関数)
(1)
y=x2にx=2を代入→A(2、4)
y=1/3x2にx=3を代入→B(3、3)
CDに長さはAとBのy座標の差だから、4-3=1
(2)
説明問題。
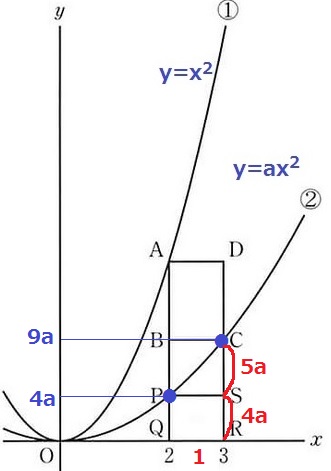
y=ax2にx=2、3を代入。
PとCのy座標はそれぞれ4a、9aとなる。
CS=5a、PS=1だから、長方形BPSCの面積は5a
SR=4a、PS=1だから、長方形PQRSの面積は4a
5a≠4aなので、2つの長方形の面積は等しくならない。
(3)

aを変えるとC(BC)が変動する。
CとDのy座標が等しい→BCがADに接した場合を考える。
A(C)のy座標は4。
y=ax2にx=3、y=4を代入。
4=32a
a=4/9
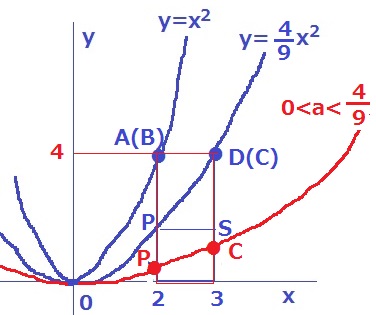
0<a<4/9、すなわち、傾きを4/9より小さくするとグラフの開きは大きくなる。
Cのy座標はDより小さい。
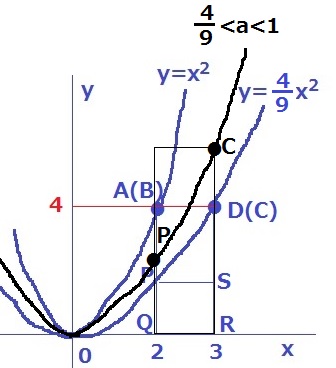
4/9<a<1のとき、すなわち、傾きを4/9より大きくするとグラフの開きは小さくなる。
Cのy座標はDより大きい。
ア…4/9、イ…小さい、ウ…大きい
(4)
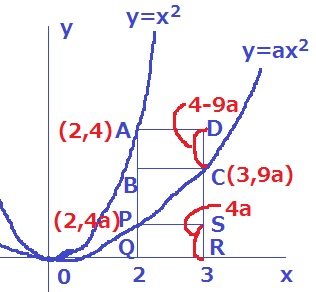
長方形の横はともに1なので、縦の長さであるCDとRSが等しくなれば面積は一緒。
座標を確認。A・C・Pのy座標さえ得られれば立式できる。
4-9a=4a
13a=4
a=4/13
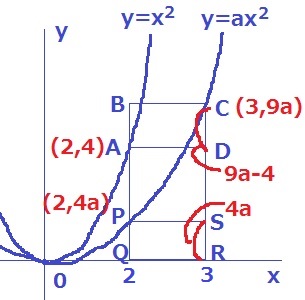
もう1つは前問を手がかりになる。
それは、BCがADよりも上にきた場合。
9a-4=4a
5a=4
a=4/5
a=4/13、4/5
(5)
難しい。
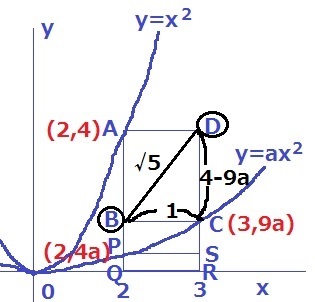
Bを中心に半径√5の円の中に長方形APSDを収納する。
A座標は(2、4)で固定。
傾きaを変えるのでCとPが位置を変え、BはC、SはPに連動する。
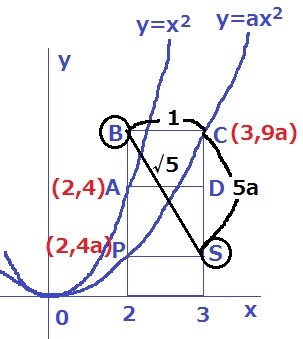
サボはaの最大値から考えました。
aの値が大きくなると、y=ax2はすぼまってy=x2に近づいていく。
BCはADより上にある。
x=2のときのP、x=3のときのCのy座標の距離は長くなり、
長方形BPSCは縦に細長くなっていく。
長方形APSDを円の中に収めるには、Bから最も遠いSに着目する。
すなわち、BS=√5となる。
BC=1、△BCSで三平方→CS=2
CとPのy座標の差から、CS=5a
5a=2
a=2/5
今度はaの最小値を求めにいく。
aの値が小さくなると、y=ax2は広がってy=x2から離れていく。
BCはADより下にある。
PとCのy座標の距離は短くなり、長方形BPSCは横に広がっていく。
先ほどのように斜辺√5の直角三角形で三平方をすると、y座標の差(縦方向)は2になる。
Aのy座標が4だから、BはAQの中点にある(CはDRの中点)
PSはx軸より上にあるので、Cのy座標との差はSよりDのほうが大きい。
長方形APSDを円の中に収めるには、Bから最も遠いDに着目する。
AとCのy座標の差から、CD=4-9a
4-9a=2
a=2/9
最も小さな値・・・a=2/9、最も大きな値…a=2/5
●講評●
大問1
(3)標本の抽出方法の誤り。3年以外が結果に反映されていない点を述べる。
(4)円周角定理の逆はサラっと使いこなせるようにしておきたい。
(6)角の二等分線にこだわり過ぎないように。円周角でも半分にできる。
大問2
(2)三角形ができるパターンが16通りもあるので、過不足なく調べあげるのは大変だった。
大問3
(1)『100人少なかった』はここでは使わない。
(2)金額の等式が長い。粘り強さが求められる。
大問4
(2)イ△ABCの面積から△ACGにどうつなげるか勝負。
大問5
面白い問題であった。
(3)y=ax2のグラフを広げたりすぼめたりすると四角形がどう変化するか。
頭の中でイメージする必要がある。
(5)さらなる思考力が求められる。
√5はBから最も遠い頂点との距離になる。
最も遠い頂点はどこになるか、シミュレーションを重ねる。



コメント