2019年度　愛媛県公立高校過去問【数学】解説

平均25.0点（50点満点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
（－24）÷６＝－４

（２）
－２/７＋１/３＝１/21

（３）
－（２ｘ－ｙ）＋３（－５ｘ＋２ｙ）
＝－２ｘ＋ｙ－15ｘ＋６ｙ
＝－17ｘ＋７ｙ

（４）
（９ａ²＋６ａｂ）÷（－３ａ）
＝－３ａ－２ｂ

（５）
（３√２－１）（２√２＋１）－４/√２
＝（12＋３√２－２√３－１）－２√２
＝11－√２

（６）
（ｘ＋４）²＋（ｘ＋５）（ｘ－５）
＝（ｘ²＋８ｘ＋16）＋（ｘ²－25）
＝２ｘ²＋８ｘ－９

大問２（小問集合）

（１）
ｘ＝２を放り込む。
２²－５・２＋ａ＝０
ａ＝６

（２）
Ａ＝１　Ｂ＝なし
Ａ＝２　Ｂ＝１
Ａ＝３　Ｂ＝１、２
Ａ＝４　Ｂ＝１、２、３
Ａ＝５　Ｂ＝１～４
Ａ＝６　Ｂ＝１～５
計15通り

全体…６×６＝36通り
15/36＝５/12

（３）
80個中、白が５個、黒が75個。
白：黒＝５：75＝１：15
白が200個だから、黒の数は、200×15/１＝3000個

（４）
展開図に直して、直角三角形ＡＥＨで三平方。
ＡＨ＝√（10²＋３²）＝√109ｃｍ

（５）
回転の中心を作図する。
対応する点Ａ－Ｐ、Ｂ－Ｑ、Ｃ－Ｒを結び、
いずれかの２本の垂直二等分線を描く。
その交点がＯとなる。

（６）
方程式。過程も記述する。
基本料金と超過料金は互いに直接関連しないので、
求めたい先月の基本料金をｘ円、先月１ｍ³あたりの超過料金をｙ円として連立を組む。
先月の使用量は25ｍ³。超過料金は25－８＝17ｍ³から。
ｘ＋17ｙ＝4260…①

今月は先月と使用量は同じだが、値上げの影響を受けて水道料金が4260＋495＝4755円となった。
1.2ｘ＋17（ｙ＋15）＝4755…②

①②を加減法で17ｙを削除すると、ｘ＝1200
代入で、ｙ＝180となる。
先月の基本料金…1200円、先月の１ｍ³当たりの超過料金…180円

大問３（正方形）

（１）
ルールの確認。
まず、短い辺で正方形をつくっていく。

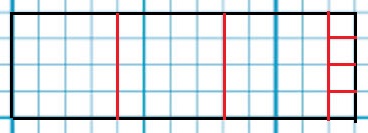
赤線が答え。
４マスずつで、最後の１マスは１×１の正方形４つ。

（２）
前問と同じ。１個目は８×８。

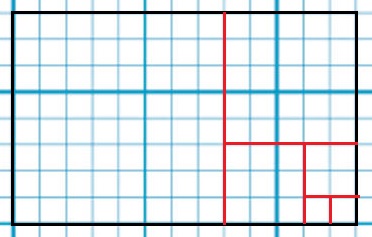
やってみるとこんな感じになる。
１辺の長さは８→５→３→２→１。
長い辺－短い辺＝次の立方体の１辺の長さ。
６個

（３）①
最初は３×３。
もう１つも３×３しかない。
縦３横６⇒ｂ＝６

②
15枚の正方形がすべて合同のパターンを考える。
１辺が３マスなので、長方形全体の横の長さｂ＝３×15＝45

次に末尾をいじる。

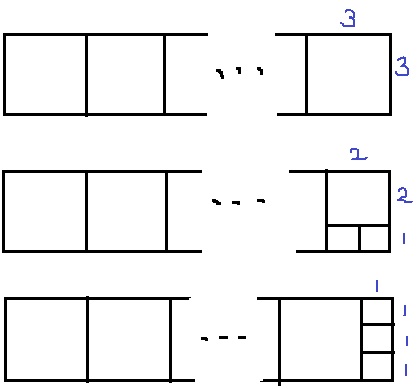
最後を２×２にして、１×１を２個くっつける。
ここで３個消費するので、３×３の正方形は15－３＝12個ある。
ｂ＝３×12＋２＝38

また、１×１を３個つけることもできる。
同じく３個消費し、３×３の正方形は12個。
ｂ＝３×12＋１＝37
ｂ＝37、38、45

大問４（関数）

（１）
ｙ＝ａｘ²のグラフに、（２、２）を放り込む。
２＝４ａ
ａ＝１/２

（２）
最大値　ｘ＝５のとき、ｙ＝25
最小値　ｘ＝０のとき、ｙ＝０
０≦ｙ≦25

（３）①
問題文を読解すると、四角形ＰＱＲＳは長方形。
Ｐのｘ座標をｔとして座標調査。

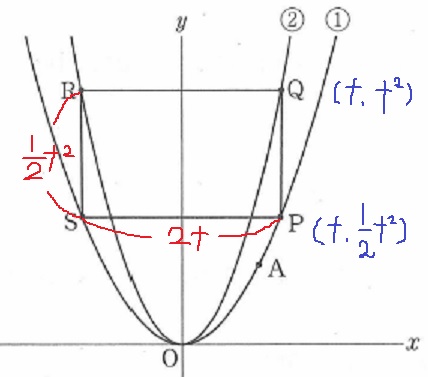
横が２ｔ、縦が１/２ｔ²となる。
周囲の長さは、（１/２ｔ²＋２ｔ）×２＝ｔ²＋４ｔ

②ア
前問の式を用いる。
ｔ²＋４ｔ＝60
ｔ²＋４ｔ－60＝（ｔ－６）（ｔ＋10）＝０
ｔ＞０より、ｔ＝６

イ
座標はＰ（６、18）、Ｑ（６、36）となる。
四角形ＰＱＲＳは長方形なので、これを２等分する直線は長方形の真ん中を横切る。

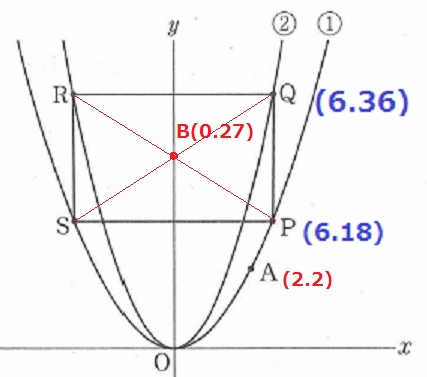
対角線の交点をＢとおく。
Ｂのｙ座標、はＰとＱのｙ座標の平均⇒Ｂ（０、27）

ＡＢの傾きを算出。
Ｂ→Ａ
右に２、下に25だから、－25/２

大問５（平面図形）

（１）
△ＥＩＣ≡△ＥＪＤの証明。

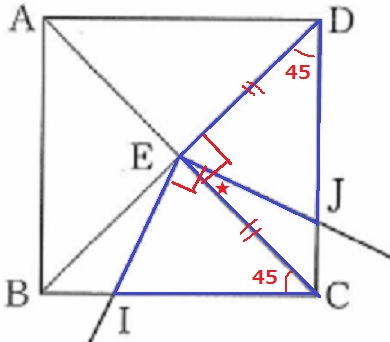
・正方形の対角線は各々の中点で交わる。
・２つの45°
・正方形の対角線は直交する＋正方形の内角の１つ
⇒２つの90°からあいだの∠ＣＥＪをひく。
以上、１辺両端角相等で合同。

（２）

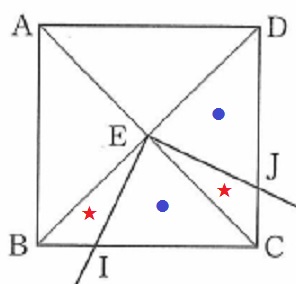
前問から、●が合同。
直角三角形ＥＢＣとＥＣＤも正方形の４分の１ずつで合同。
ということは、直角三角形から●を同じようにひいた★も合同。
２つの正方形が重なった四角形ＥＩＣＪは、直角三角形ＥＢＣと面積が等しい。

正方形ＡＢＣＤの面積…③×③＝⑨
正方形ＥＦＧＨの面積…④×④＝⑯
重なったところ…⑨×１/４＝○９/４

全体の面積は、⑨＋⑯－○９/４＝○91/４
これが182ｃｍ²に相当する。

正方形ＡＢＣＤの面積は、182×⑨/○91/４＝72
よって、その１辺の長さは、√72＝６√２ｃｍ

＠余談＠
Ｅを中心に正方形ＥＦＧＨをクルクル回しても、
重なった部分の面積は一定で、正方形ＡＢＣＤの４分の１。

（３）
大きい正方形の１辺は、６×４/３＝８ｃｍ
△ＥＩＣと△ＥＫＦに刮目。

45°＋●より２角相等→∽
ＥＣは小さい正方形の対角線の半分→３√２
△ＥＩＣ：△ＥＫＦ＝３√２：８
面積比は２乗。（３√２）²：８²＝18：64＝９：32

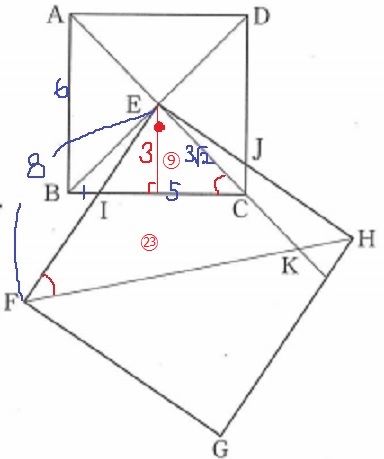
四角形ＩＦＫＣ＝○32－⑨＝○23

△ＥＩＣは底辺５、高さ３。
５×３×１/２×○23/⑨＝115/６ｃｍ²
公立高校入試解説ページに戻る