平均59.9点(前年比;+6.2点)
問題はこちら→リセマムさん
2019年長崎A問題の解説はこちら。
大問1(小問集合)
(1)
(√2-√6)2+12/√3
=2-2√12+6+4√3
=8
(2)
12a2b3÷4/3ab2×(-2b)2
=36ab3
(3)
S=1/2(a+b)h ←両辺を2倍して()を展開
2S=ah+bh ←aのみ左辺へ
ah=2S-bh
a=2S/h-b
(4)
(x+1)(x+4)=2(5x+1)
x2-5x+2=0
因数分解ができないので、解の公式を適用。
x=(5±√17)/2
(5)
√(67-2n)の根号を外すと整数になる。
nは自然数なので、67-2nは81(=92)以下。
つまり、√(67ー2n)<√81(=9)だから、根号を外すと8以下の整数。
ルートの中の67-2nは、8以下の整数の平方数になる。
nの値をできるだけ小さくするので、67-2nの値をできるだけ大きくする。
67は奇数。2nは偶数。
奇数-偶数=奇数だから、8以下の平方数で最も大きい奇数の平方数49が怪しい。
67-2n=49
n=9
(6)
①y=-x+100(一次関数)
②y=πx2(y=ax2)
③y=4x(比例)
④y=6/x(反比例)
反比例はxとyの積が比例定数aで一定。
⑤y=3x(比例)
(7)
円錐の側面になる扇形の中心角…360×底面の半径/母線
360×2/5=144°
(8)

角の二等分線は、2本の直線から等距離にある点の集合。
円の中心Pは3本の線分から等距離にある。
∠ABCと∠DCBの二等分線の交点が中心Pとなる。
大問2(小問集合2)
(1)① (Aと違い、確率を求める)
カードを取り出し方は、4×4=16通り
引き分けは(1、1)か(4、4)の2通り
2/16=1/8
②
【全体-引き分け=勝敗がつく】
1-1/8=7/8
③
前問の考えを利用する。
陽平と明子の勝率を等しくするには、勝敗がつく場合が偶数でなければならない。
カードを1枚追加すると、全体の取り出し方は5×4=20通り
全体(偶数)-勝敗がつく(偶数)=引き分け(偶数)
すなわち、引き分けの場合も偶数でなくてはならない。
A(1・4・5・6)
B(1・3・4・7)
現状、引き分けは(1、1)(4、4)のみ。
1か4を追加すると、片方に1か4が2つ偏るので引き分けのパターンが奇数になる。
3・5・6・7を追加すると、(1、1)(4、4)に加え、
追加したカードと同じ数の組み合わせで引き分けが3パターンになってしまう。
つまり、追加するカードは箱A・箱Bのどちらにも入っていない【2】と確定できる。
A(1・4・5・6)
B(1・3・4・7)
箱Bに最も強い7のカードがあるが、他が弱いのでBの方が弱そう。
2は弱いカードなので、箱Aに2を入れる。
*計算すると、2を入れる前、陽平が勝つ場合は8通り、明子が勝つ場合は6通り。
2のカードを箱Aに入れると、陽平は(2、1)で勝つが、
明子は(2、3)(2、4)(2、7)で勝つので、両者9通りのパターンで勝利する。
確率でいえば、いずれも9/20で勝利する。
(2)① (以下、Aと同じ)
10人の中央値⇒5番目と6番目の平均値。
5番目は4点、6番は5点なので中央値は4.5点
②
4点は2人なので、2÷10=0.2
相対度数は分数ではなく、小数であらわす。
③
範囲(レンジ)=最大値-最小値
A…範囲が広い。平均値4.5点
B…範囲が狭い。4と5の間を対称の軸とすると左右対称→平均値4.5点
平均値はAとBで同じだが、範囲はAの方がBより大きい。
*高校数学ではデータのバラつき度合を分散で求めます。
(3) (Aと同じ)
抽出した120個のうち、アルミは75個だった。
全体:アルミ=120:75=8:5
4800×5/8=3000個
大問3(関数)
(1)
y=1/2x2にx=-2を代入。
y=1/2×(-2)2=2
(2)
同様にBの座標を求める。B(4、8)
A(-2、2)⇒B(4、8)
右に6、上に6なので傾きは1
Aから右に2、上に2でABがy軸と交わる。
切片の座標は(4、0)
AB:y=x+4
(3)
原点を通過する。
最小値 x=0のとき、y=0
最大値 x=4のとき、y=8
0≦y≦8
(4)①
OB:y=2x
Qのy座標…y=2×5=10
Rのy座標…y=1/2×52=25/2
PQ:QR=10:25/2-10=4:1
②
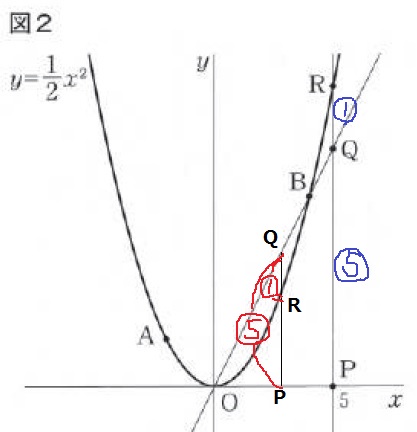
PQ:QR=1:5となる瞬間は、Bをはさんで2つある。
注意点はBのx座標より下にくるとき、QとRの位置が逆転する!
青①:⑤
PQ:RQ=2x:1/2x2-2x=5:1
2x=5(1/2x2-2x)
5/2x2-12x=0
5x2-24x=x(5x-24)=0
x=0だとPQ、QRの長さが0になってしまうので、
x=24/5
赤①:⑤
PQ:QR=2x:2x-1/2x2=5:1
2x=5(2x-1/2x2)
5/2x2-8x=0
5x2-16x=x(5x-16)=0
x>0より、x=16/5
x=16/5、24/5
大問4(空間図形)
(1) (以下、Aと同じ)
【ねじれの位置】⇒平行でもない、かつ延長しても交わらない。
DFとEFとCFで3本。
(2)
4×4÷2×8=64cm3
(3)
錐の体積は柱の3分の1。
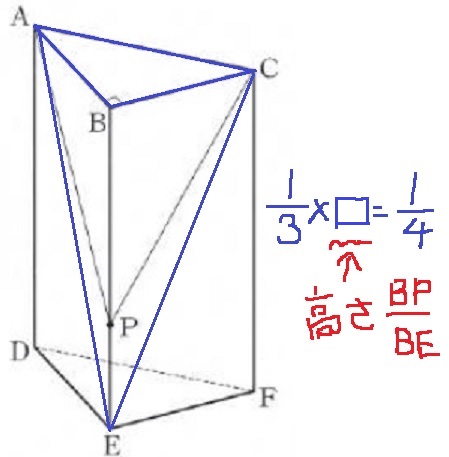
三角錐E-ABCが三角柱の体積の1/3倍にあたる。
ここから高さを調節する。
最終的に三角柱の体積の1/4倍になるので、高さを□とおくと、
1/3×□=1/4
□=1/4÷1/3=3/4
BEを3/4倍すればBPになる。
BP=8×3/4=6cm
(4)
水面の高さがは5cm。
水のあるところの体積:水がないところの体積=⑤:③
容器を傾けても体積比は変化しない。
四角形ADFCを底面とするので、高さを△ABC方向から見る。
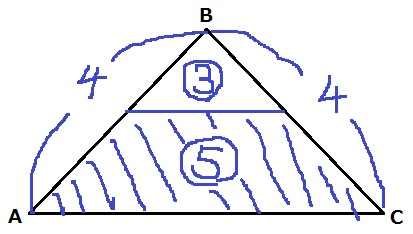
柱なので奥行きが等しいから、体積比は底面積の比と同じ。
水あり:水なし=⑤:③

面積比は相似比の2乗。
2乗して③となる→□√3
2乗して⑧となる→□√8=□2√2
AB:GB=2√2:√3
Bから垂線をおろし、交点をI・Hとする。
△BHCは直角二等辺三角形だから、1:1:√2でBH=4×1/√2=2√2cm
△BGI∽△BAHより、BH:IH=2√2:2√2-√3
2√2×(2√2-√3)/2√2=2√2-√3cm
大問5(平面図形)
(1)
△ABHで三平方。
AH=√(32-12)=√8=2√2cm
(2)①
△ABC∽△BECの証明。
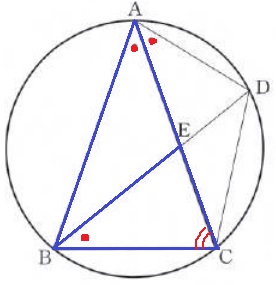
∠ACB=∠BCE(共通角)
∠BAC=∠CAD(仮定)
∠CAD=∠CBE(弧CDに対する円周角)
2角が等しい→∽
②
前問の∽を利用。
BC:EC=AC:BC=3:2
EC=2×2/3=4/3cm
AE=3-4/3=5/3cm
AE:EC=5/3:4/3=5:4
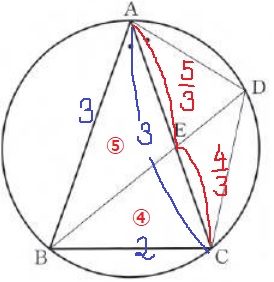
△ABE:△EBC=5:4
△ABCの面積の5/9倍が△ABEとなる。
2×2√2÷2×5/9=10√2/9cm2
(3)
∠AEBと等しい角を選ぶ。
対頂角である∠DECは、さすがに選択肢にない。
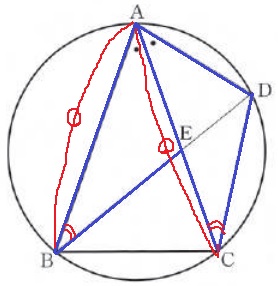
△ABEと△ACDに着目、1辺と両端角が等しいので合同。
∠AEBに対応する∠ADCが答え。③
(4)
(2)と(3)をクリアしていれば、すぐ出せる。
(3)より、△ACDは△ABEと合同。
(2)より、△ABE=10√2/9
△ACD=10√2/9
これに△ABCを足せばいい。
2×2√2÷2+10√2/9
=28√2/9cm2
大問6(整数)
(1)
28の約数。
1、2、4、7、14、28
(2)
3√3=√27、2√6=√24
√24<√26<√27
2√2<√26<3√3
(3)
a2+b2=102を満たす、自然数a、bの組合せを答える。
aとbは1以上9以下なので、
1~9の平方数1・4・9・16・25・36・49・64・81のなかから、
我が100になる組合せを調べると、36+64=100
ア:6、イ:8
@別解@
3:4:5でピタゴラス数となるので、
2倍して6:8:10からa=6、b=8といける。
(4)
【3以上の奇数aの平方数が、連続する2つの自然数b、cの和と等しくなると、
a2+b2=c2が成り立つ】
41は奇数なので、a=41が解答の1つ。
もう1つは連続するb・cのうちのいずれかが41。
(例題をみるとcが奇数なので、cが41ではないかと推測しておく)
◆a=41
連続する2つの自然数をn、n+1とおく。
412=n+(n+1)
2n=1680
n=840
(a、b、c)=(41、840、841)
◆bかc=41
例題ではcが奇数なので、cに41を当てはめてみる。
bはcの1つ前の数なので40。
a2=40+41=81
a=9
(a、b、c)=(9、40、41)
(9、40、41)と(41、840、841)
(5)
整数の証明問題。
連続する3つの自然数はn、n+1、n+2となる。
これらをa、b、cにあてはめる。
n2+(n+1)2=(n+2)2
n2-2n-3
=(n-3)(n+1)0
nは自然数なのでn>0
n=3
ピタゴラスの定理(三平方の定理)a2+b2=c2において、
a、b、cが連続する自然数でa=3だから、
連続する3つの自然数の組合せからなるピタゴラス数は(3、4、5)



コメント
4の(2)って4×4÷2×4で32cm^3じゃないんですか
質問者です。誤って投稿してしまい、すいません(>人<;) 2016年度と間違ってました!
いえいえ(´ω`)
何かわからないことがありましたら、また書き込んで下さい。