2021年度　鳥取県公立高校入試問題過去問【数学】解説

平均24.4点（前年比；－1.3点）

問題はコチラ→ＰＤＦファイル
出題範囲の削減はなし。

大問１（小問集合）

（１）①　98.9％
３＋（－５）
＝３－５
＝－２

②　94.4％
－２/３×（－３/４）
＝１/２

③　84.2％
５√６ー√24＋18/√６
＝５√６－２√６＋３√６
＝６√６

④　91.0％
３（ｘ＋ｙ）－２（－ｘ＋２ｙ）
＝３ｘ＋３ｙ＋２ｘ－４ｙ
＝５ｘ－ｙ

⑤　70.6％
－４ａｂ²÷（－８ａ²ｂ）×３ａ²
＝３/２ａｂ

（２）　79.1％
（３ｘ－ｙ）²
＝９ｘ²－６ｘｙ＋ｙ²

（３）　89.3％
ａ²＋４ａ
＝（－３）²＋４×（－３）
＝９－12
＝－３

＠別解＠
ａ²＋４ａ
＝ａ（ａ＋４）
＝－３×１
＝－３
大して時間は変わらない。

（４）　84.2％
ｘ²＋５ｘ－６
＝（ｘ＋６）（ｘ－１）

（５）　41.8％
（５－３ｘ）/２－（ｘ－１）/６＝１　←６倍
３（５－３ｘ）－（ｘ－１）＝６
15－９ｘ－ｘ＋１＝６
10ｘ＝10
ｘ＝１

（６）　78.0％
ｘ²－ｘ－１＝０
解の公式を適用して、
ｘ＝（１±√５）/２

（７）　33.9％

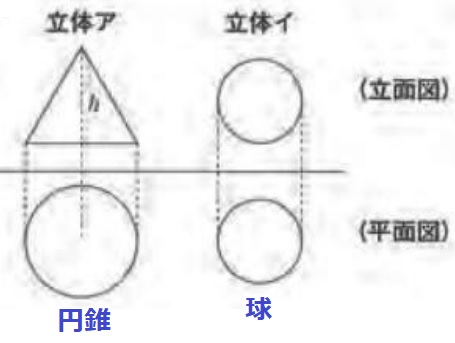
立面図は正面から、平面図は上からみた図。
アは円錐、イは球。
【球の体積Ｖ＝４/３πｒ³】
イの体積…４/３π×３³＝36πｃｍ³
立体アの底面積が16πｃｍ²なので、高さは36π×３÷16π＝27/４ｃｍ

（８）①　81.9％
ｙ＝ａｘ²に（ｘ、ｙ）＝（６、12）を代入。
12＝６²ａ
36ａ＝12
ａ＝１/３

②　54.2％
ａ＞０だから、下に凸のグラフ。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－４のとき、最大値ｙ＝１/３×（－４）²＝16/３
０≦ｙ≦16/３

（９）　60.5％（部分点率28.8％）
答案では理由も記述する。
全体は６×６＝36通り
積ａｂが12未満の組み合わせを調べる。
ａ＝１のとき、ｂ＝１～６で６通り
ａ＝２のとき、ｂ＝１～５で５通り
ａ＝３のとき、ｂ＝１～３で３通り
ａ＝４のとき、ｂ＝１～２で２通り
ａ＝５のとき、ｂ＝１～２で２通り
ａ＝６のとき、ｂ＝１で１通り
12未満は19通り。
12以上は36－19＝17通り
19/36＞17/36だから、12未満の方が起こりやすい。（ア）

（10）　65.0％（部分点率0.6％）

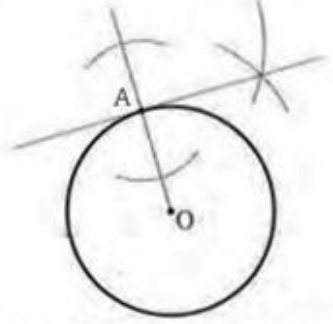
接線の作図。
半直線ＯＡをひく。
Ａを通る半直線ＯＡの垂線が円Ｏの接線である。

大問２（データの活用）

（１）読み取り…88.7％、作図…82.5％
表１のＡ市から36～38℃、38～40℃を頑張って探す。
度数は５日と１日。
ａ…５、ｂ…１

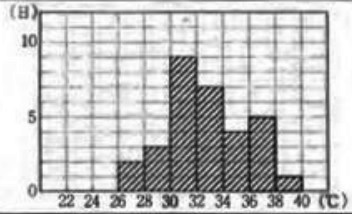
５マスと１マスをヒストグラムに追加する。

（２）　83.6％
最頻値（モード）は最もあらわれている値。
30～32℃の階級値である31℃。

（３）　19.8％！
ア：Ａ市の度数分布表では26～28℃の度数が２日となっているが、
　それが26～27℃の範囲にあるかはわからない。×
イ：Ａ市の度数が４の階級は34～36℃で、この階級値は35℃。×
ウ：31個の中央値（メジアン）は16番目。
　Ａ市は32～34℃→33℃、Ｂ市は30～32℃→31℃でＢ市が低い。〇
エ：範囲（レンジ）＝最大値－最小値。階級値で計算すると37－25＝12℃×
オ：８÷31＝８/31←分母が分子の４倍より小さいので、１/４（0.25）より大きい。〇
ウ・オ

大問３（空間図形）

ア～ウ…92.1％、エ～カ…70.1％、キ…55.9％、ク…60.5％、ケ…64.4％
最初は立方体について。

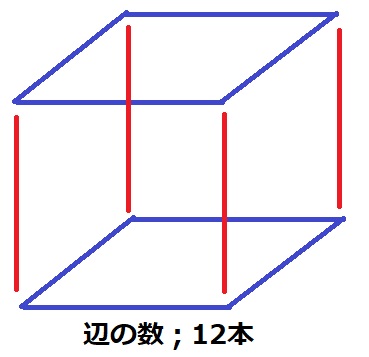
天井と床の正方形の各辺、高さが４本ずつ。
立方体の辺の数…４×３＝12本（ア）
頂点の数…８個（イ）、面の数…６個（ウ）

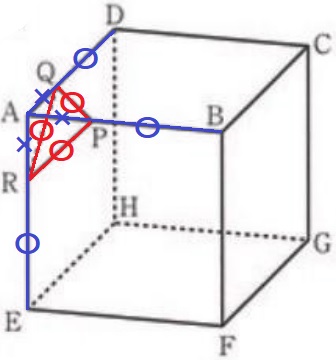
個数の変化をみる。
辺は×の線分が消えるが、これは〇の辺の一部であるため減少はない。
増加分は〇。辺の数は全体で３本増える。よって、15本（エ）
頂点の数はＡがなくなるので－１。新たに頂点Ｐ、Ｑ、Ｒが増える。
頂点の数は全体で＋２だから10個（オ）
面の減少なし。新たに面ＰＱＲが追加されるので、＋１して７個。

辺は＋３、頂点は＋２、面は＋１。
これが立方体の頂点８ヶ所で起こる。
辺の数…12＋３×８＝36本（キ）
頂点の数…８＋２×８＝24個（ク）
面の数…６＋１×８＝14個（ケ）
ア…12、イ…８、ウ…６、エ…15、オ…10、カ…７、キ…36、ク…24、ケ…14

＠＠＠

ちょうたい多面体より。
本問の多面体は立方体の頂点を切り落とした切頂六面体（切頂立方体）という。
正三角形が８個、八角形が６個の十四面体である。
リンク先で展開図をプリントアウトできます。

＠オイラーの多面体定理＠
【穴のない多面体（ドーナツではない）において、
頂点の数－辺の数＋面の数＝２が成り立つ】
↑数学の世界では有名な定理です。
切頂六面体では、24－36＋14＝２

大問４（方程式）

（１）　29.4％！
試合時間はａ分が10回→10ａ分
休憩は間の数で９回あり、そのうち１回は昼休憩40分、８回がｂ分。
合計して、10ａ＋８ｂ＋40

（２）　26.6％！
前問の式を利用する。
午前９時から午後３時⇒６時間＝360分
ｂ＝５を代入して、
10ａ＋８×５＋40＝360
10ａ＝280
ａ＝28
試合時間は28分。

（３）①　21.5％！（部分点率18.1％）
ソフトの試合時間ｙはサッカーの試合時間ｘの1.6倍だから、ｙ＝1.6ｘ

サッカーの試合時間…６ｘ分
あいだの休憩…５回あるので４×５＝20分
昼休憩…40分
ソフトの試合時間…４ｙ分
あいだの休憩…３回あるので４×３＝12分
この合計が５時間20分＝320分
６ｘ＋20＋40＋４ｙ＋12＝320
６ｘ＋４ｙ＝248

ｙ＝1.6ｘ　…①
６ｘ＋４ｙ＝248　…②

②　18.1％！
先の連立を解く。
①を②に代入して、
６ｘ＋6.4ｘ＝12.4ｘ＝248
ｘ＝20
サッカーの試合時間は20分。

大問５（平面図形）

（１）　23.7％！
１辺９ｃｍの正三角形の面積。

正三角形を半分に割ると、内角が30°－60°－90°の直角三角形。
辺の比は１：２：√３だから、高さは９√３/２ｃｍ。
面積は、９×９√３/２÷２＝81√３/４ｃｍ²

（２）１…85.3％、２…75.1％、３…60.5％
△ＡＤＣ≡△ＢＰＣの証明。

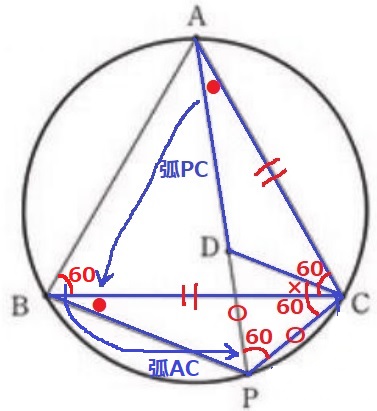
正三角形ＡＢＣの１辺より、ＡＣ＝ＢＣ
弧ＰＣに対する円周角で、∠ＰＡＣ＝∠ＰＢＣ（●）

弧ＡＣに対する円周角で、∠ＡＢＣ＝∠ＡＰＣ＝60°
△ＰＣＤの注目！頂角が60°の二等辺三角形は正三角形。
正三角形ＰＣＤの内角で、∠ＰＣＤ＝60°
正三角形ＡＢＣの内角で、∠ＡＣＢ＝60°
∠ＡＣＤ＝60－∠ＢＣＤ（×）＝∠ＢＣＰ
１辺両端角が等しいので、△ＡＤＣ≡△ＢＰＣ
１…イ、２…エ、３…１辺と両端角が等しい

（３）　18.1％！

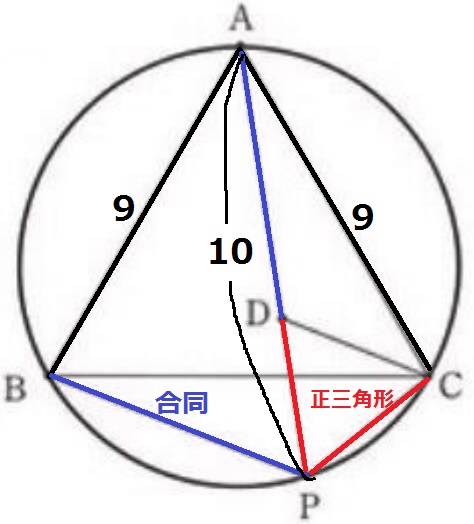
前問の合同と正三角形を再利用。
△ＡＤＣ≡△ＢＰＣより、対応する辺でＡＤ＝ＢＰ
正三角形ＰＣＤより、ＤＰ＝ＰＣ
ＢＰ＋ＰＣ＝ＡＤ＋ＤＰ＝10ｃｍ
四角形ＡＢＰＣの周の長さは、９＋10＋９＝28ｃｍ

（４）　0.0％!!!
（１）で△ＡＢＣの面積を求めているので、△ＡＢＣと△ＣＤＱの面積比が知りたい。

前問のとおり、ＢＰ＝ＡＤ＝②、ＰＣ＝ＤＣ＝①
対頂角と60°で２角相等→△ＢＰＱ∽△ＣＤＱ
ＤＱ：ＱＰ＝【１】：【２】より、
△ＣＤＱの面積を１とすると、△ＣＰＱは２

ＤＰ＝①
ＡＤ：ＤＰ＝②：①から、△ＡＣＤの面積は６

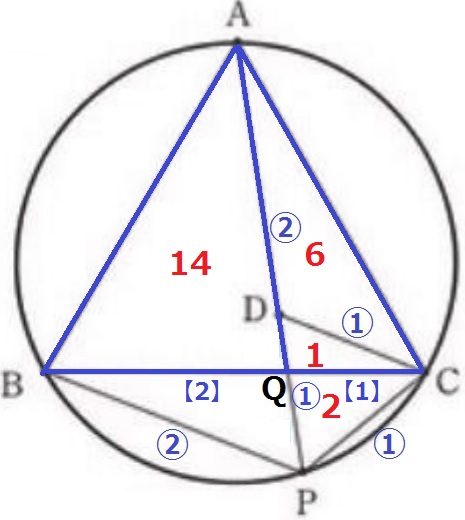
先ほどの相似で、ＢＱ：ＱＣ＝【２】：【１】だから、
△ＡＢＱ：△ＡＣＱ＝２：１で、△ＡＢＱの面積は14
正三角形ＡＢＣは21だから、△ＣＤＱの面積は、
81√３/４×１/21＝27√３/28ｃｍ²

大問６（数量変化）

（１）　33.9％

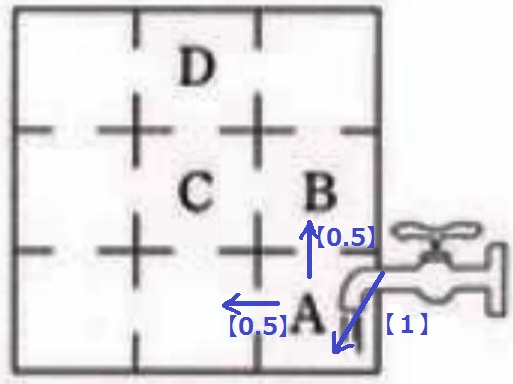
Ａに流入する量を【１】（１分で1000ｃｍ³）とする。
Ａが満水になると、隣の２部屋に【0.5】ずつの水が入る。
Ｂに流入する水の量は、半分の毎分500ｃｍ³

（２）　20.9％！

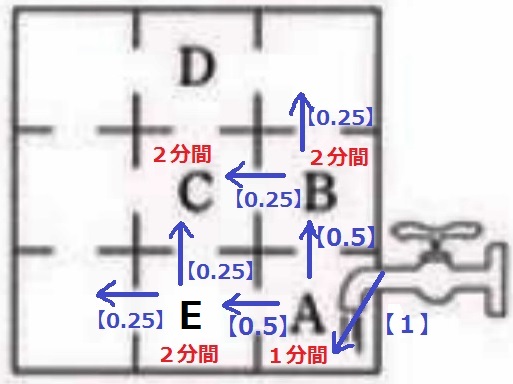
Ａの左をＥとする。
【１】の流入では１分で満水になる。
１分後にＡからＢとＥの部屋に流入。
【0.5】ずつ入るので、２分で満たされる。
その後、ＢとＥから４つの出口にそれぞれ【0.25】ずつ水が出ていく。
Ｃには合計【0.5】流入するので、Ｂと同じく２分で満水になる。
１＋２＋２＝５分後

（３）①　2.3％!!

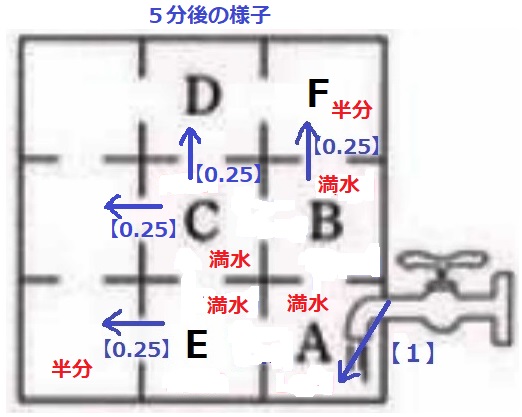
Ｂのうえの部屋をＦとする。
Ｂが満水した３分後にＦ、Ｅの左に水が流入する。
このとき、水の出口は４つなので各々【0.25】ずつ。
Ｃが満水した５分後に、Ｆには【0.25】×２＝【0.5】流入したので、
Ｆの残りは【0.5】。さらに２分後の７分後にＦが満水。

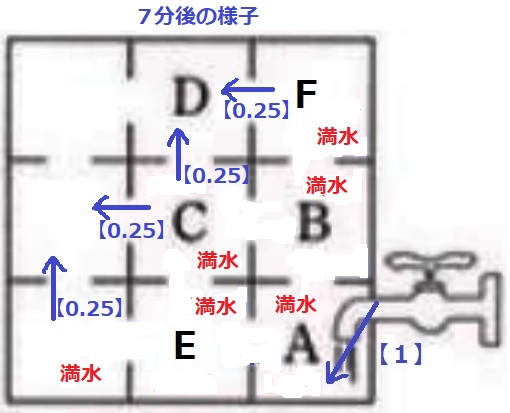
７分後のＤは、Ｃから【0.25】×２分＝【0.5】流入済み。
ここからＦが合流するので、残り【0.5】を【0.5】の流入で埋める→８分後に満水。

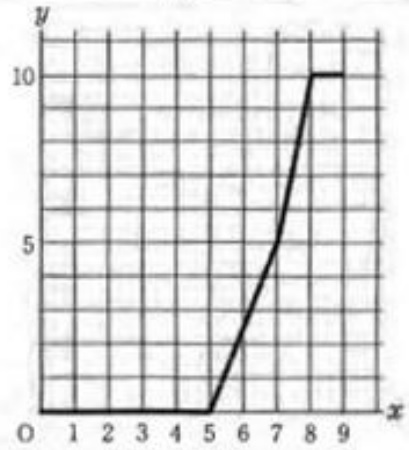
↑まとるめとこうなる。
Ｄには、まずＢから５分後に流入。
このときは【0.25】の流入で２分間で半分の５ｃｍまで入る。
７分後にＦからも流入するので【0.5】となり、傾きが２倍に。
８分後にＤは満水、以降は10ｃｍをキープする。

②　5.1％!!
前問のグラフを完成できればとれる。
７～８分後の１分間で５ｃｍ上昇する。
高さ５ｃｍから＋３ｃｍとなる時間は、１分×３/５＝３/５分
７＋３/５＝38/５分後