2019年度　兵庫県公立高校過去問【数学】解説

平均51.7点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）　98.5％
（－５）＋（－２）
＝－５－２＝－７

（２）　94.3％
（－６ｘｙ²）÷（－３ｘｙ）
＝２ｙ

（３）　97.3％
５√３－√27
＝５√３－３√３
＝２√３

（４）　87.3％
ｘ²－３ｘ－４
＝（ｘ＋１）（ｘ－４）＝０
ｘ＝－１、４

（５）　93.1％
反比例の比例定数ａはｘｙ。
ａ＝２×（－３）＝－６

（６）　92.0％

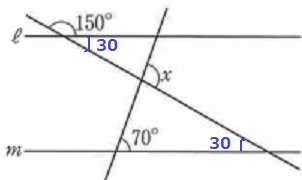
30°を錯角でおろして、外角定理。
ｘ＝70＋30＝100°

（７）　66.4％
三平方で底辺の半径を求める。
√（３²－２²）＝√５
√５×√５×π×２×１/３＝10π/３ｃｍ³

（８）　81.4％
円の中心点の作図方法を選ぶ。
円周上の任意の点を結び、垂直二等分線の交点が円の中心となる。
ウ

大問２（数量変化）

（１）　50.0％
Ａモードは燃費100％で200ｋｍ走行できる。
アは燃費20％を消費したので、
200×20％＝40

（２）　50.0％
グラフからＢモードでは、
80－10＝70％の燃費で250－40＝210ｋｍ走行できる。
210×100/70＝300ｋｍ

（３）　22.7％！
160ｋｍを時速60ｋｍで走る時間は、
160÷60＝８/３＝２時間40分
Ａモードでは20％の燃料の消費で40ｋｍ走行できたので、
160ｋｍでは、20×160/40＝80％の燃料を使う。

Ｂモードは100％で300ｋｍ走行するので、
残りの20％では、300×20/100＝60ｋｍ走行できる。
60ｋｍを時速40ｋｍで走る時間は、
60÷40＝３/２＝１時間30分
したがって、２時間40分＋１時間30分＝４時間10分

（４）　10.5％！
最短時間で走行する→できるだけＡモードで走る。
燃料100％でＡは200ｋｍしか走れない。
燃料１％でＡは２ｋｍ、Ｂは３ｋｍ走ることができる。
ということは、Ａの１％をＢの１％に変えると１ｋｍ多く走れる。
〔燃料100％Ａモード200ｋｍ〕の状態から、走行距離を＋50ｋｍ伸ばすには、
燃料50％分をＡ→Ｂに変えればいい。
つまり、Ａモードの燃料は50％。
200×50/100＝100ｋｍ

大問３（関数）

（１）　68.2％
ｙ＝１/２ｘ²に放り込む。
Ｂ（２、２）
〔原点Ｏ→Ｂ〕上に２、右に２だから傾きは１。

（２）　64.2％
Ａの座標は（－４、８）
ＡとＢを通る直線の式を求める。
〔Ａ→Ｂ〕右に６、下に－６⇒傾きは－１
ｙ＝－ｘ＋ｂに代入して切片ｂを求めると、
ｙ＝－ｘ＋４
よって、Ｃ（０、４）
△ＯＡＣ＝４×４÷２＝８ｃｍ²

（３）①　41.7％
△ＢＣＤの底辺は、８×２÷２＝８
Ｄのｙ座標は正なので、ＤはＣから上に８。
ｙ＝４＋８＝12

②　5.6％!!
ＡＤの傾きを調べると、
〔Ａ→Ｄ〕右に４、上に４で、
ＡＤの傾きはＯＢと同じで平行。

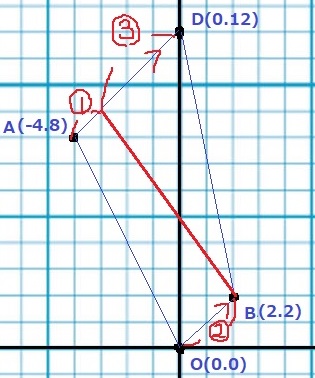
上底と下底で、和を等しくすれば二等分になる。
ＡＤを１：３に内分する点→（－３、９）

大問４（平面図形）

（１）　57.6％
Ａ、Ｂ、Ｃは円周の３分の１。
∠ＡＯＢ＝360×１/３＝120°

（２）　57.6％

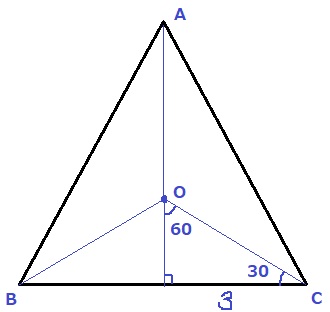
90－60－30の直角三角形（１：２：√３）を利用して、
ＯＣ（半径）＝３×２/√３＝２√３ｃｍ

（３）　79.6％
△ＡＢＱと△ＣＢＰの合同を証明する。

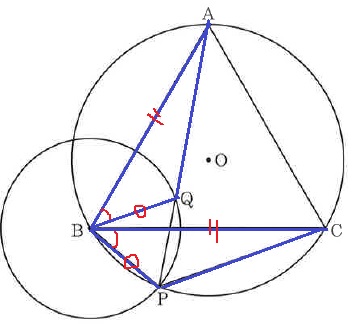
正三角形の１辺と半径。
あいだの角は∠ＡＢＣ＝∠ＰＢＱ＝60°から∠ＣＢＱをひくことで、
∠ＡＢＱ＝∠ＣＢＰと導く。
∠ＰＢＱ＝60°は、円周角定理から、∠ＡＣＢ（60°）を∠ＡＰＢに移動させ、
△ＢＰＱが二等辺三角形であることから、∠ＢＱＰ＝60°となり、
三角形の内角の和から、∠ＰＢＱ＝60°となる。（△ＢＰＱは正三角形）
i…ウ、ii…エ

（４）　0.7％!!!
Ｐの位置を定める。
前問の△ＡＢＱ≡△ＣＢＰがヒントになる。
Ｐが移動してもこの関係は変わらない。
△ＣＢＰの面積が最大になるとき、Ｐはどこにあるか？

ＢＣを底辺とすると、高さを最も高くするには、
ＰがＢＣから最も離れている場所。
すなわち、円の真下にＰがあればいい。

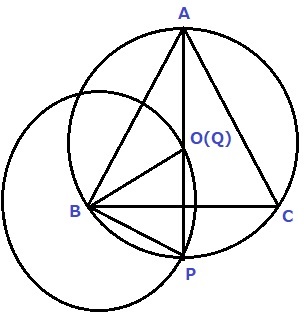
△ＢＰＱは正三角形。
ということは、ＱがＯと重なり、２つの円は半径が同じ。

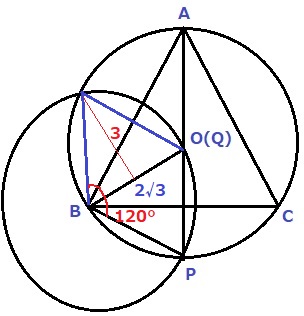
ＢＯを対称の軸として、△ＯＢＰを反対側に持ってくると、
合同の正三角形が現れる。（同じ半径で３辺が等しい）
正三角形の１辺は半径の２√３で、高さは１：２：√３より３。
２つの円が重なる部分は、半径２√３で中心角120°の扇形２つから、
正三角形２つ分をひけばいい。
２√３×２√３×π×120/360×２－２√３×３÷２×２
＝８π－６√３ｃｍ²

大問５（場合の数）

（１）①　87.0％
１枚ずつ３回取り出す。
百の位…５通り、十の位…４通り、一の位…３通り。
５×４×３＝60通り

②　68.5％
十の位は２。百の位…４通り、一の位…３通り。
４×３＝12通り
12/60＝１/５

③　6.3％!!
百の位の候補は、２、３、４、７、９。
この５枚の平均は（２＋３＋４＋７＋９）÷５＝５
十の位も同様。一の位も同様。
よって、５５５。
位ごとに独立して考えるのがミソ。

（２）　6.5％!!
今度は１枚を除いて平均を出したら、111小さくなった。
555－111＝444
百の位の候補は何かを除いた４枚。
４枚の平均で４になるから、総和は４×４＝16。
２、３、４、７、９のうち、４枚を選んで総和が16になる組み合わせは、
２、３、４、７。
よって、裏のカ－ドは９。

大問６（規則）

①②（①～④まで67.2％）
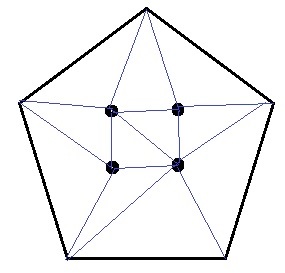
ルールに沿って線分を描く。

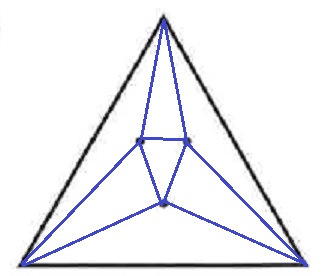
↑わかりやすいのはこれかな？
①９、②７

③④
五角形でチャレンジ。

③14、④11

⑤⑥　6.8％!!
規則を一般化する。
会話文から角度に注目するといいらしい。

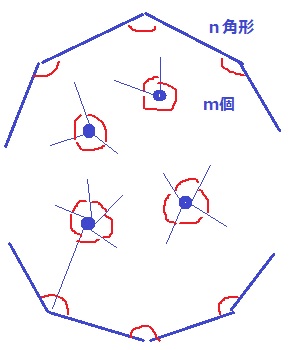
中にある三角形の内角の合計は、
外側のｎ角形の内角の和＋ｍ個の点の周りの角（360°）の和に等しい。
ｎ角形の内角の和→180（ｎ－２）
ｍ個の点の周りの角の和→360ｍ
これら２つの角の和を、三角形の内角の和である180で割れば、
ｎ角形のなかにできる三角形の個数ｘがでる。
ｘ＝｛180（ｎ－２）＋360ｍ｝/180
＝（360ｍ＋180ｎ－360）/180
＝２ｍ＋ｎ－２　…⑤

ｘ個の三角形の辺の個数は、三角形が３辺だから３ｘ。
３ｘ＝３（２ｍ＋ｎ－２）＝６ｍ＋３ｎ－６
外側の辺はｎ角形の辺と共有しているので除外。
ｎ角形の辺の数→ｎ個
６ｍ＋３ｎ－６－ｎ＝６ｍ＋２ｎ－６
内側の辺は隣り合う三角形同士で辺を共有するので÷２をすれば、線分の個数ｙがでる。
ｙ＝（６ｍ＋２ｎ－６）÷２＝３ｍ＋ｎ－３　…⑥

⑦　25.8％！
先ほどの式でｎに20、ｍに19を代入。
ｙ＝３×19＋20－３＝24
線分は24本。24本目を５人で引くので、
24÷５＝５・・４
余り４だから、Ｄさんが24本目を引くことになる。→Ｄ…⑦
公立高校入試解説ページに戻る