2022年度　石川県公立高校入試問題過去問【数学】解説

平均47.2点（前年比；－1.4点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア
２－５
＝－３

イ
９÷（－３）－４²
＝－３－16
＝－19

ウ
６ａ²ｂ³÷３/５ａｂ²
＝10ａｂ

エ
（ｘ＋２ｙ）/５－（ｘ＋３ｙ）/４
＝｛４（ｘ＋２ｙ）－５（ｘ＋３ｙ）｝/20
＝（４ｘ＋８ｙ－５ｘ－15ｙ）/45
＝（－ｘ－７ｙ）/20

オ
√12＋２√６×１/√８　←√２で約分。√４＝２
＝２√３＋２√３/２
＝３√３

（２）
２ｘ²－５ｘ－１＝０
解の公式を適用して、ｘ＝（５±√33）/４

（３）

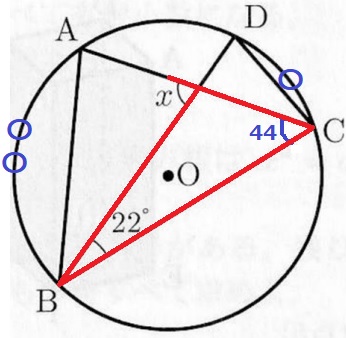
円周角の大きさは弧の長さに比例する。
∠ＡＣＢ＝22×２＝44°
赤線で外角定理→ｘ＝22＋44＝66°

（４）
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加したときの変化の割合はａ（ｐ＋ｑ）
ｙ＝ｘ²だからａ＝１
ｐ＝ａ、ｑ＝ａ＋３を代入すると、
１（ａ＋ａ＋３）＝13
ａ＝５

（５）
ア＋イ＝12－（１＋４＋２）＝５人
12人の中央値（メジアン）は６番目と７番目の平均。
５番目は１回。中央値を２回にする。
●２と２の平均で中央値２回（→６番目と７番目が２回）
残りの３人は２回でも３回でも良いので３通り。

●１と３の平均で中央値２（６番目が３）
残り５人は全員３回になので１通り。
合計４通り。

大問２（確率）

（１）
100円硬貨の確率は48枚中27枚。
全体は320枚なので、320×27/48＝180枚

（２）
答案では説明も書く。
全体は、２³＝８通り
ａ－ｂ≧100が成り立つａとｂの組み合わせを考える。
●200－０＝200
３枚すべてが表で１通り。
●150－50＝100
１枚の50円だけが裏。50円玉は２枚あるから２通り。
合計３通り、確率は３/８。

大問３（数量変化）

（１）
Ａ車は50Ｌで、１ｋｍ走ると0.1Ｌ消費する。
50－70×0.1＝43Ｌ

（２）

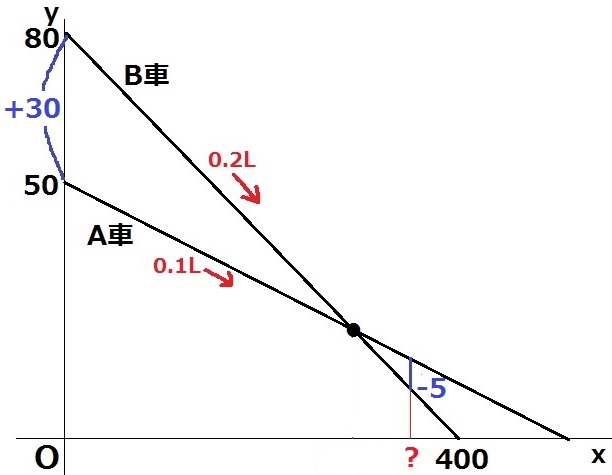
Ａ－Ｂ＝５Ｌとなるのは、交点の後ろである。
Ｂは１ｋｍで0.2Ｌずつ消費するので、燃料タンクの容量は400×0.2＝80Ｌ
出発時のＡとＢの差は、80－50＝30Ｌ

ＡとＢは毎秒0.1Ｌずつ差が埋まっていく。
Ｂ－Ａの差が＋30Ｌから－５Ｌになるので、30－（－５）＝35Ｌの差が拡大したときが答え。
35÷0.1＝350ｋｍ

（３）
Ｃは200ｋｍ走ると、240－190＝50Ｌの燃料を消費する。
【50Ｌで200ｋｍ】⇒【１Ｌで４ｋｍ】
1800ｋｍ走るには、1800÷４＝450Ｌの燃料が必要。

容量は240Ｌ。全部使い切ったあとに全補給すれば計480Ｌ入るので足りる。
すなわち、240×４＝960ｋｍ地点で補給すればいい。

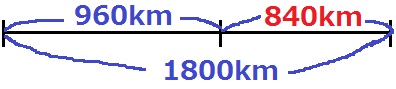
960ｋｍで補給して、残りの1800－960＝840ｋｍを走る。
この順番は逆でも良い。
つまり、先に840ｋｍを走ってから全補給して、残りの960ｋｍを走る。
答えは840ｋｍ以上、960ｋｍ以下。

大問４（方程式）

答案では、方程式を立てて途中式も書く。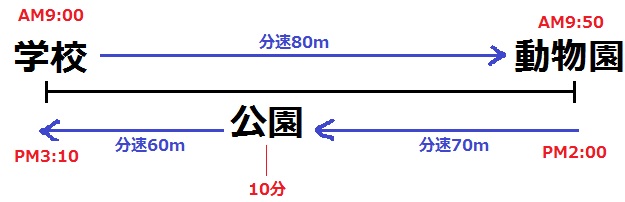
問題文の情報を図に描く。
行きは速さと時間が確定済みなので、学校～動物園の道のりは、80×50＝4000ｍ

学校～公園をｘｍ、公園～動物園をｙｍとする。
道のりで等式。ｘ＋ｙ＝4000　…①
時間で等式。休憩時間を除くと移動時間は合計60分。
ｘ/60＋ｙ/70＝60　…②

連立を解けばいいが、②がイヤすぎる(´Д｀)
②を60倍して、ｘ＋６/７ｙ＝3600　…③
①－③で、１/７ｙ＝400
ｙ＝2800
①に代入、ｘ＝4000－2800＝1200ｍ
学校―公園…1200ｍ、公園―動物園…2800ｍ

大問５（作図）

①ＰＡ＝ＰＢ
ＰはＡとＢから等距離にある⇒ＡＢの垂直二等分線

問題は②△ＰＡＢ＝△ＰＣＤ
ＡＢ＝ＣＤ。これらを底辺としたとき、面積が等しい→高さも等しい。

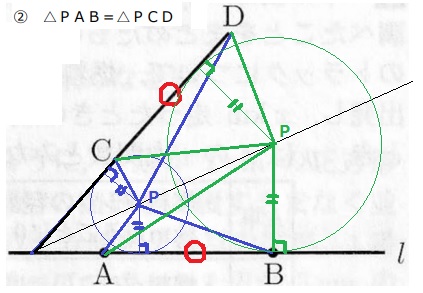
つまり、底辺ＡＢと底辺ＣＤからの距離が等しい線分上にＰが存在する。
２直線から等しい距離にある点の集合は角の二等分線である。

①ＡＢの垂直二等分線
②ＡＢとＣＤを延長、この２直線のなす角の二等分線
これらの交点がＰとなる。

大問６（平面図形）

（１）

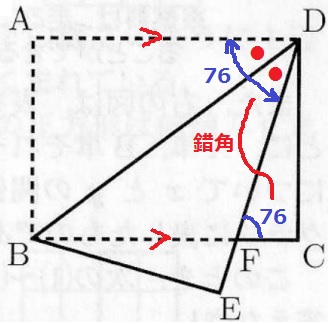
ＡＤ//ＢＣの錯角で、∠ＡＤＦ＝76°
折り返しで、∠ＡＤＢ＝∠ＢＤＦ（●）
∠ＢＤＦ＝76÷２＝38°

（２）
△ＡＢＫ≡△ＨＩＧの証明。

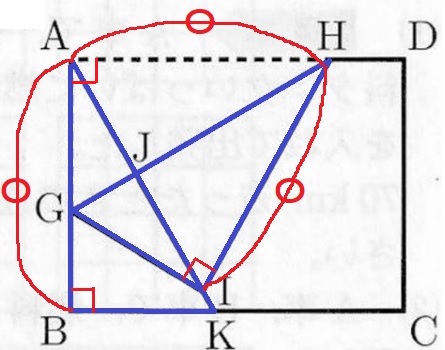
仮定と折り返しで、ＡＢ＝ＨＡ＝ＨＩ
∠ＡＢＫ＝90°
折り返しで、∠ＨＡＧ＝∠ＨＩＧ＝90°
ここまではわかりやすいが、もう１つが指摘しづらい。

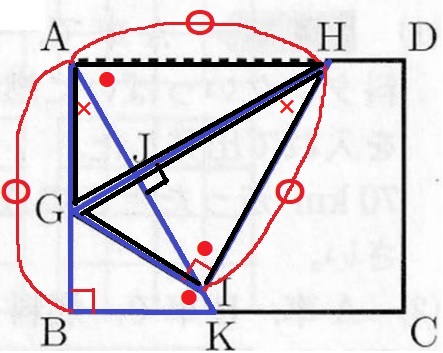
折り返しで、△ＨＡＧ≡△ＨＩＧ
ＨＧを対称の軸とするとＡに対応する点がＩだからＡＩ⊥ＨＧ
∠ＨＪＩ＝90°

∠ＢＡＫ＝×、∠ＡＫＢ＝●とする。
ＡＤ//ＢＣの錯角で、∠ＨＡＪ＝●
対称性から、∠ＨＡＪ＝∠ＨＩＪ＝●（二等辺ＨＡＩの底角でもいい）
△ＨＩＪの内角から、∠ＩＨＧ＝180－（90＋●）＝×
１辺と両端角が等しいので合同。

（３）

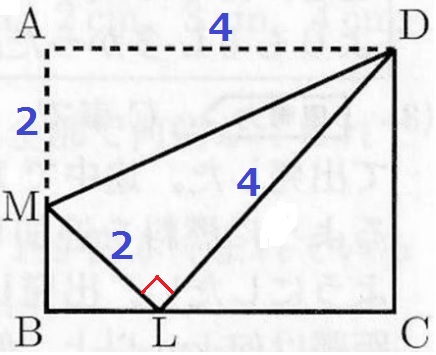
△ＤＭＬ＝４ｃｍ²。ＭＬ＝４×２÷４＝２ｃｍ
折り返しで、ＡＭ＝２ｃｍ

長方形ＡＢＣＤの面積を求めたい。
横は４ｃｍだから、縦が知りたい。

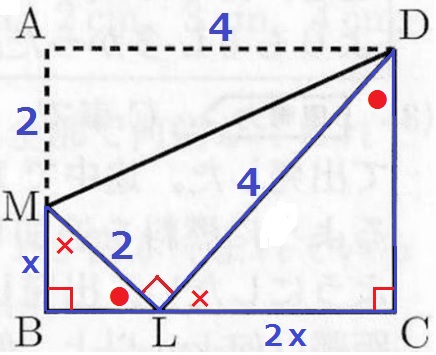
そこで、ＭＢをｘとする。
●＋×＝90°で等角を示すと、２角相等で△ＭＢＬ∽△ＬＣＤ
相似比は、ＭＬ：ＬＤ＝①：②
ＬＣ＝２ｘ

ＢＬ＝４－２ｘ
ＣＤ＝２（４－２ｘ）＝８－４ｘ
長方形の縦の長さで等式→ｘ＋２＝８－４ｘ
ｘ＝６/５
ＡＢ＝２＋６/５＝16/５ｃｍ
長方形の面積は、４×16/５＝64/５ｃｍ²

大問７（空間図形）

（１）

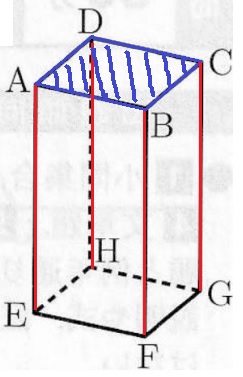
天井に垂直な辺は、直方体の高さにあたる４辺。
辺ＡＥ、辺ＢＦ、辺ＣＧ、辺ＤＨ

（２）
答案では途中の計算も書く。

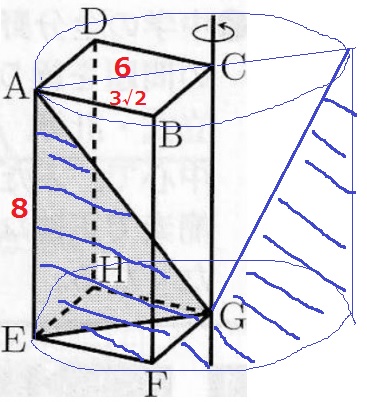
求積すべき立体は円柱から円錐をくり抜いた形である。
△ＡＢＣは正方形ＡＢＣＤの半分で直角二等辺三角形。
辺の比は１：１：√２→ＡＣ＝３√２×√２＝６ｃｍ

円柱の体積を③とすると円錐は÷３で①、残りの体積は②。
６×６×π×８×②/③＝192πｃｍ³

（３）
ここも答案に途中式いるの？(´ﾟωﾟ`;)

ＤＲ＝ＢＰ＝●としたとき、ＡＳ＝ＣＴ＝●となるようなＳ、Ｔをとる。
ＴはＣＱの中点で、Ｓ・Ｐ・Ｔ・Ｒは底面ＥＦＧＨから等距離にある。
青の三角錐Ａ―ＳＰＲと赤の三角錐Ｑ―ＴＰＲは底面積（△SPR≡△TPＲ）と高さが等しく合同。
青を赤に入れると、水を平らに均すことができる。

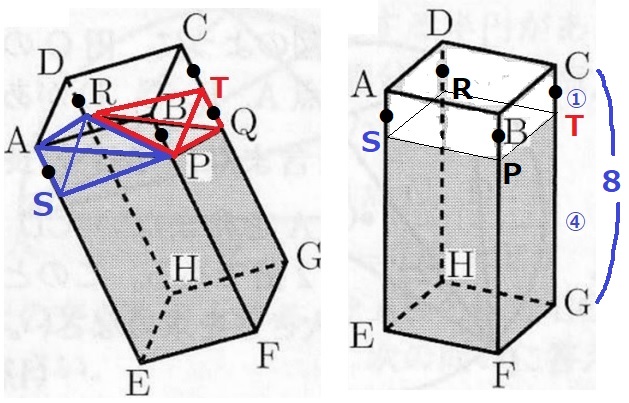
四角柱の体積を⑤とすると、残っている水は④。
ＣＴ：ＴＧ＝①：④
ＣＱ＝ＣＴ×２＝②
ＣＱの長さは、８×②/⑤＝16/５ｃｍ