平均29.9点(前年比;-3.6点)
問題はこちら→リセマムさん
出題範囲の縮小は、三平方の定理の活用と標本調査。
大問1(計算)
(1)
2+(-9)
=2-9
=-7
(2)
7/5×(-10)
=-14
(3)
6-4÷(-2)
=6+2
=8
(4)
4√3+√12
=4√3+2√3
=6√3
(5)
6ab2÷b×3a
=18a2b
(6)
-(-3x+y)+2(x+y)
=3x-y+2x+2y
=5x+y
大問2(小問集合)
(1)
4x+3=x-6
3x=-9
x=-3
(2)
2x-3y=2 …①
x+2y=8 …②
サボは、②×2-①でやりました。
x=4、y=2
(3)
(x-3)2
=x2-6x+9
(4)
x2+2x-8
=(x+4)(x-2)
(5)
2x2+3x-1=0
解の公式を適用。
x=(-3±√17)/4
(6)
3×3×π×60/360
=3/2πcm2
(7)
不等式。
『7より大きい』のでイコールは含まない。
4x-y>7
(8)
30人の中央値は15番目と16番目の平均。
→7時間以上~8時間未満の階級に含まれる。
階級値は7と8の平均で7.5時間。
(9)
ア:√9<√10<√16。√10は3より大きく、4より小さい。
イ:2乗するとaになる数をaの平方根という。6の平方根は±√6。×
ウ:1辺が√2の正方形の面積は√2×√2=2。〇
エ:”平方根を求めよ”とは違う問題である。
√16>0なので、√16=4。√16≠-4×
ウ
大問3(確率)
(1)
出目が同数→(1、1)(2、2)…(6、6)の6通り
(2)①
(a、b)=(x、y)とすると、
(x、y)=(6、5)(5、4)(4、3)(3、2)(2、1)の5通り
全体は6×6=36通りだから、確率は5/36
②
どの2辺が等辺になるか→どの1辺が等辺にならないかで場合分け。

OPが等辺でない→P(6、6)
APが等辺でない→P(0、6)だが、x=0ゆえ無し。
OAが等辺でない→x=3上にPは6個ある。
7通りだから、確率は7/36
大問4(平面図形)
(1)
角の二等分線の作図。教科書レベル。
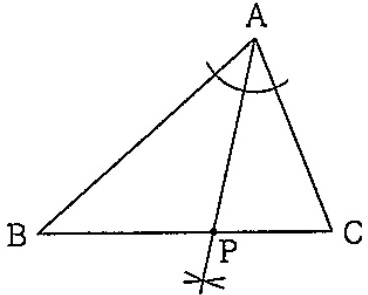
Aに針を合わせてヒョコ。
交点に針を合わせてヒョコヒョコ。
∠Aの二等分線とBCとの交点がP。
(2)①
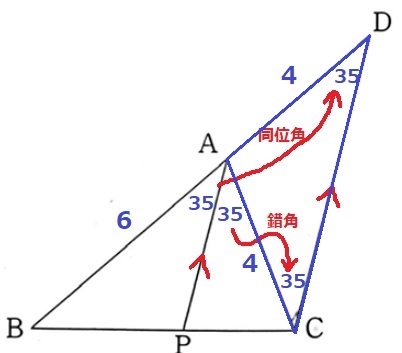
AP//DCより、錯角で∠ACD=∠CAP=35°
②
同位角で、∠ADC=35°
△ACDは2つの底角が等しく、二等辺三角形。
AD=AC=4cm
@余談@

角の二等分線の定理に出てくる形なので、見たことある人はいたはず。
2角相等で△ABP∽△DBC
BA:AD=BP:PC
AD=ACで順番を整理すると、
AB:AC=BP:PCとなる(角の二等分線の定理)
大問5(整数)
(1)
23=20+3
=10×2+3
35=30+5
=10×3+5
①…3、②…10、③…5
(2)
十の位がa、一の位がbの2桁の自然数は10a+b
位を入れ替えた数は10b+a
(10a+b)+(10b+a)
=11a+11b
=11(a+b)
a+bは整数だから、11(a+b)は11の倍数である。
④…10a+b、⑤…10b+a、⑥…a+b
(3)
Xの十の位をa、一の位をbとする。
仮定よりa>b
前問の式を利用すると、
X+Y=11(a+b)=132
a+b=12
a>bより、(a、b)=(9、3)(8、4)(7、5)
Xは75、84、93
大問6(数量変化)
(3)
(2)より、PがAB上を動く0≦x≦5は、y=x2で増加する。
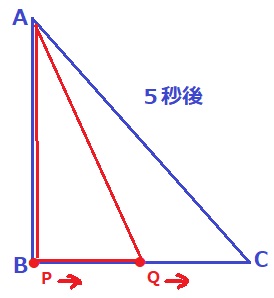
5秒後以降はBC上でPがQを追いかける。
高さは変わらず底辺だけが短くなるから、一次関数で減少する。
10秒後にPとQが同時にCへ着き、y=0となる。
イ
(4)
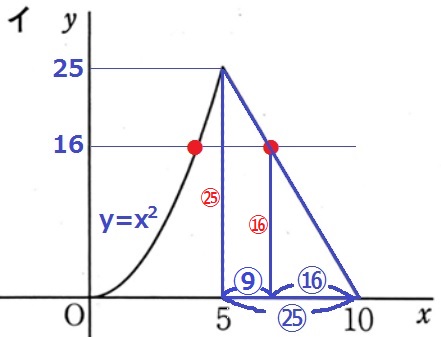
2つある。
y=x2にy=16を代入。x>0から、x=4
もう1つは、相似比が25:16である三角形の相似を利用する。
5+5×⑨/㉕=5+1.8=6.8
4秒後と6.8秒後
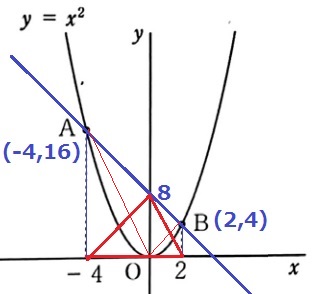
大問7(関数)
(1)
y=x2にx=-4を代入。
y=(-4)2=16
(2)
A(-4、16)→B(2、4)
右に6、下に12だから、傾きは-12/6=-2
切片はBから左に2、上に4移動して、4+4=8
y=-2x+8
(4)
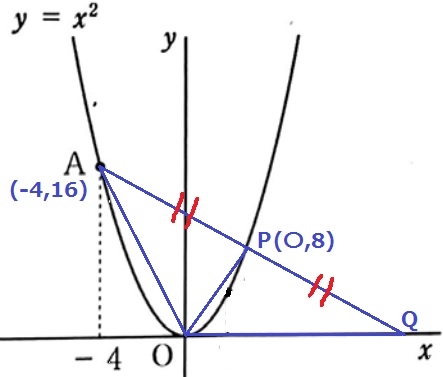
△OPAと△OPQは底辺がともにAQ上にある。
面積が等しい→AP=PQ
Pのy座標は、16÷2=8
これをy=x2に代入すると、8=x2
x>0より、x=2√2
P(2√2、8)
大問8(平面図形2)
(1)
正五角形の内角の1つの大きさ。
覚えている人はすぐ書ける。
n角形の内角の和は、180(n-2)°
180(5-2)÷5=108°
(2)
△ACD∽△AFEの証明。
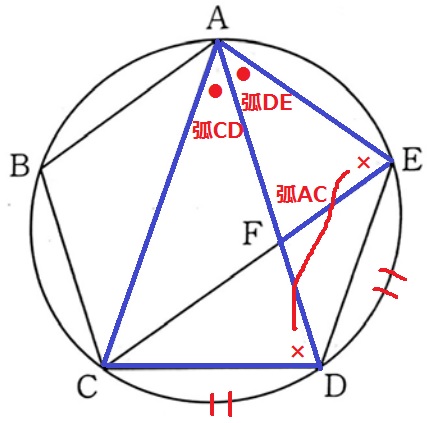
長さの等しい弧に対する円周角は等しい。
弧CD=弧DEより、∠CAD=∠FAE
弧ACに対する円周角より、∠ADC=∠AEF
2角相等で∽
@空欄の解答@
円周角
弧ACに対する円周角は等しいから、∠ADC=∠AEF
2角が等しい
(3)

正五角形の対称性より、△ACDは二等辺三角形(左右対称)
これと相似にあたる△AFEも二等辺なので、AF=AE=1cm
△AFEと△CFDに注目すると、
AE=CDと等しい円周角から、1辺と両端角が等しく合同。
△ACD∽△CFDより、DF=xcmとおくと、
【AD:CD=CD:FD】
(x+1):1=1:x
外項と内項の積で、
x(x+1)=1
x2+x-1=0
解の公式を適用して、x=(-1±√5)/2
x>0より、x=(-1+√5)/2
AD=(-1+√5)/2+1
=(1+√5)/2cm
@余談@
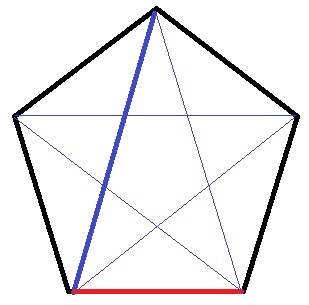
正五角形の1辺を1としたとき、対角線の長さは(1+√5)/2。
1:(1+√5)/2は幾何的に美しい比率とされる黄金比で自然界にもみられる。
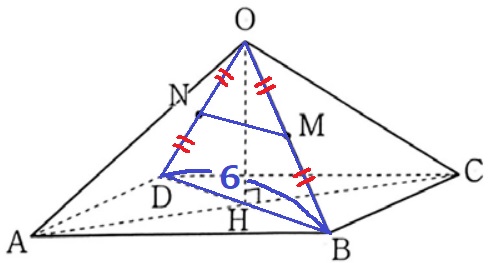
大問9(空間図形)
(2)①

面OACを正面にして眺めると、A—M—PとA—N—Pが一直線で重なり、
MとNは同じ高さにある→Mの後ろにあるQも同じ高さ。
MがOB、NがODの中点であるように、QはOHの中点である。
OQ=4÷2=2cm
②
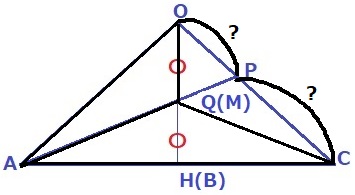
QCに補助線。
OP:PCは、△OAQ:△CAQの面積比にあたる。
(共通辺AQを底辺にすると、高さの比がOP:PCだから)
△OAQと△CAQの面積比を求める。
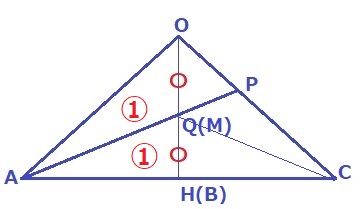
前問より、QはOHの中点。OQ=QH
△OAQ=△QAH=①とする。
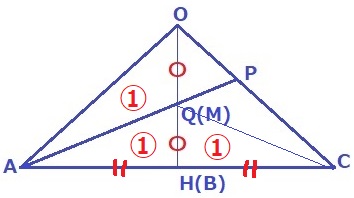
HはACの中点。AH=HC
△QAH=△QCH=①
△OAQ:△CAQ=OP:PC=1:2
③
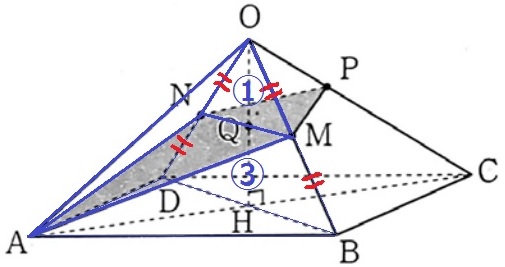
四角錐O―ABCD(全体)の体積は、6×6÷2×4÷3=24cm3
ポイントは、三角錐O―ABDと三角錐O―CBDの半分に分ける。
三角錐O―ABDは12cm3
底面を△OBDに捉えなおすと、三角錐A―OBD:三角錐A―OMNの体積比は、
底面積の比である△OBD:△OMNに相当する。
三角錐A―OMNの体積は、12×①/④=3cm3
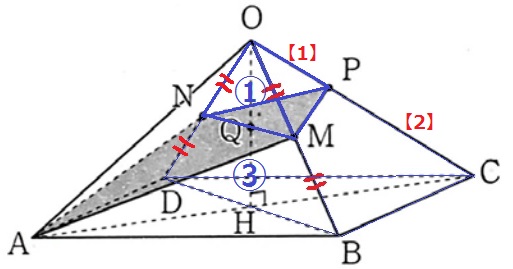
反対側の三角錐C―OBD(12cm3)と三角錐P―OMNの体積比を考える。
底面積の比は、△OBD:△OMN=④:①
高さの比は、OC:OP=【3】:【1】
三角錐C―OBD:三角錐P―OMN
=④×【3】:①×【1】
=12:1
三角錐P―OMNの体積は、12×1/12=1cm3
したがって、四角錐O―AMPNの体積は、
三角錐A―OMN+三角錐P―OMN=3+1=4cm3
@別解@
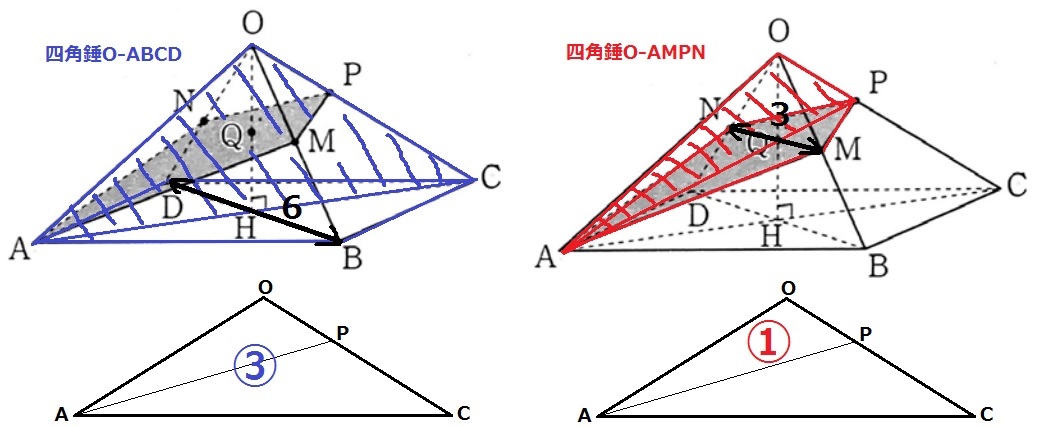
全体の四角錐O―ABCDから直接、四角錐O―AMPNの体積を求めることもできる。
△OACを底面に捉える。前問の解答より、△OAC:△OAP=③:①
△OACを中央にして上からみると、図形全体が左右対称である。
そこで、高さは△OACを基準にしたときの左右の最大幅で捉える。
四角錐O―ABCDの底面積△OACは③。高さは最大幅であるBD=6cm
四角錐O―AMPNの底面積△OAPは①。高さは最大幅であるMN=3cm(前問で解答済み)
三角錐O―AMPNの体積は、24×①/③×3/6=4cm3
大問10(文章題)
(1)
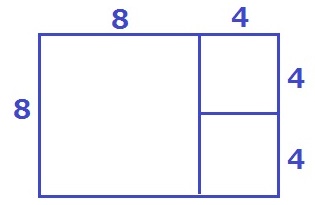
短辺8cmを1辺とする正方形を切り取ると、4×8の長方形ができる。
短辺4cmを1辺とする正方形を切り取ると、4×4の正方形が2個できて終わる。
4cm
@@
縦8cm、横12cmの長方形を同じ正方形で埋めつくす場合、
正方形の1辺の長さは8でも12でも割り切れる数、すなわち、8と12の公約数である。
正方形の1辺の最長は8と12の最大公約数だから4cmとすぐ求めることができる。
以降の解説では最大公約数を用いる。
(2)

21とnの最大公約数が7。
正方形の数は縦が3個、横が〇個で合計15個。
〇=15÷3=5
n÷7=5
n=5×7=35
(3)
221と299の最大公約数を求めて終了。
13cm
@余談@
221と299が何で割り切れるのか、迷ったときは差に注目する。
299-221=78
78の約数は【1, 2, 3, 6, 13, 26, 39, 78】
221と299はともに奇数なので偶数はバツ!
位の和が3の倍数でもない。となると、13しかない。
@余談2@
問題文の手順通りにやってみると、
221×299 ←長辺-短辺を繰り返していく
221×78
143×78
65×78
65×13
65は13の倍数なので13cmとなる。
●講評●
大問1
完答を目指そう。
大問2
時間をかけずに高得点を。
(9)平方根は2つある。
大問3
(2)②斜辺で場合分けすると、重複ミスを防ぎやすい。
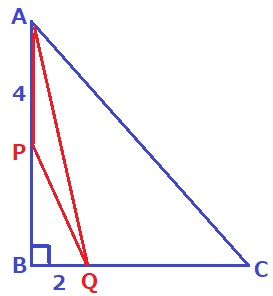
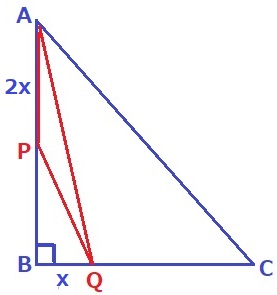
大問4
(2)②公立高校入試でも角の二等分線の定理は知っておいた方が良い。
大問5
(3)前問の考えを検討。
位の和が12で、かつ十の位が大きい組み合わせを調べる。
大問6
(4)前問のイに数値を書き込む。三角形の相似を使うと楽。
大問7
(4)Pのy座標が先に求まる。
大問8
(3)黄金比を知っていればすぐ出せるが、知らないと苦労する。
二等辺三角形の相似は見えづらいので注意。
大問9
(2)①類題を経験していないと厳しいか。
②処理は少ないが、ここも慣れが求められる。
③前問の解答が必須。難問なので解けなくても問題ない。
【底面積の比×高さの比=体積比】
大問10
9より10を先にやったほうがいいね。。



コメント