2021年度　福岡県公立高校入試問題過去問【数学】解説

平均47.6％（前年比；－8.1％）
問題はコチラ→ＰＤＦファイル
出題範囲の除外は三平方の定理の活用と標本調査。
＊三平方の定理の意味を理解し、それが証明できることを知ることは出題に含まれる。

大問１（小問集合）－75.4％

（１）　97.1％
７＋２×（－６）
＝７－12
＝－５

（２）　93.2％
３（２ａ＋ｂ）－２（４ａ－５ｂ）
＝６ａ＋３ｂ－８ａ＋10ｂ
＝－２ａ＋13ｂ

（３）　91.5％
14/√２－√32
＝７√２－４√２
＝３√２

（４）　85.1％
（ｘ＋６）（ｘ－５）＝９ｘ－10
ｘ²＋ｘ－30＝９ｘ－10
ｘ²－８ｘ－20
＝（ｘ＋２）（ｘ－10）＝０
ｘ＝－２、10

（５）　66.7％
４枚の硬貨を投げた結果→２⁴＝16通り
『少なくとも１枚は表』→全体からすべて裏の場合を引く。
すべて裏は１通りしかないから、『少なくとも１枚』は15通り。
確率は15/16

（６）　65.2％
ｙ＝１/２ｘ²はａ＞０で下に凸のグラフ。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－４のとき、最大値ｙ＝８
０≦ｙ≦８

（７）　70.9％
ｙ＝－６/ｘのグラフを描く。

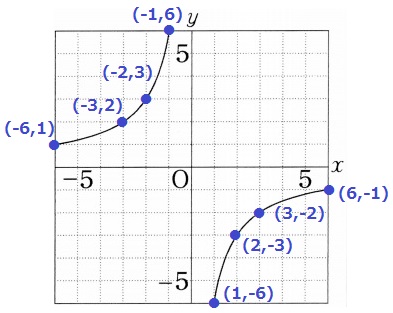
反比例なので双曲線となる。
積ｘｙは比例定数－６で一定。
ａ＜０だから、グラフは左上（第２象限）と右下（第４象限）にある。

（８）　72.5％
∠Ａ＝90°である直角三角形ＡＢＣ。
三平方の定理（辺の比が３：４：５）から、ＡＣ＝８ｃｍ

（９）　36.4％

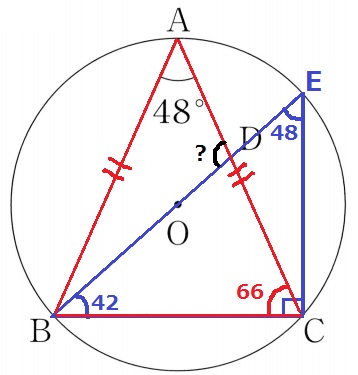
ＢＯを延長して円との交点をＥとする。
半円の弧に対する円周角∠ＢＣＥ＝90°
∠ＥＢＣ＝180－90－48＝42°
二等辺ＡＢＣの底角である∠ＡＣＢ＝（180－48）÷２＝66°
△ＢＣＤで外角定理→∠ＡＤＢ＝42＋66＝108°

大問２（データの活用）－71.2％

（１）　83.0％
図１の13ｍ以上14ｍ未満の度数は４回。
４÷30＝0..133…≒0.13

（２）　63.4％
説明問題。
中央値の場合は『中央値がふくまれる階級』
最頻値の場合は『その数値』と書くべき要素が微妙にズレている(´･_･`)

30回の中央値（メジアン）は15番目と16番目の平均。
Ａは11ｍ以上12ｍ未満の階級、Ｂは10ｍ以上11ｍ未満の階級でＡの方が遠くまで飛んでいる。

最頻値（モード）は最もあらわれている値。
Ａは9.5ｍ、Ｂは11.5ｍでＢの方が遠くまで飛んでいる。
モードが手っ取り早く書ける。

大問３（整数）－42.6％

（１）　48.9％
偶数は２ｍ。
連続する２つの偶数は２ｍと２ｍ＋２。
２ｍ（２ｍ＋２）＋１
＝４ｍ²＋４ｍ＋１
＝（２ｍ＋１）²
ｍは整数だから、２ｍ＋１は奇数である。
したがって、連続する２つの偶数の積に１を加えた数は、奇数の２乗になる。

＠余談＠

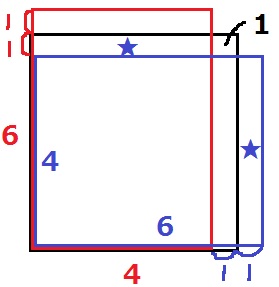
↑連続する偶数を４・６とする。
４×６の青い長方形において、
右の★を上の★に移動して＋１すると５×５の正方形になる。

（２）Ａ…50.3％、Ｂ…45.4％
偶数は２ｎ、奇数はその前後の『２ｎ＋１』や『２ｎ－１』
連続する２つの奇数は『２ｎ＋１、２ｎ＋３』や『２ｎ－１、２ｎ＋１』など。
ｎに係数のない『ｎ、ｎ＋２』は、差が２である２つの整数。

ｎ（ｎ＋２）＋１
＝ｎ²＋２ｎ＋１
＝（ｎ＋１）²
ｎ＋１はｎとｎ＋２の間の数。
”もとの２つの数の間の整数”が答えになる。
Ａ…エ、Ｂ…オ

（３）　30.6％！

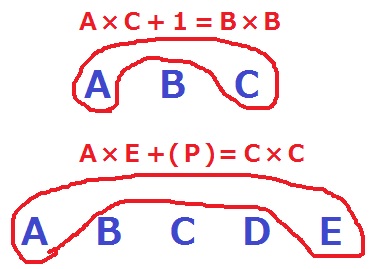
先ほどは『差が２である２つの整数』をいじくると『あいだの数』になったが、
これら３つの整数は連続する３つの整数である。
連続する３つの整数をＡ、Ｂ、Ｃとすると、Ａ×Ｃ＋１＝Ｂ×Ｂ

最終的に真ん中の数の２乗になるので、連続する５つの整数Ａ、Ｂ、Ｃ、Ｄ、Ｅで、
計算結果がＣ×Ｃとなりそうな組み合わせを探す。
中央のＣから距離が等しく、かつ±１ではないとするとＡとＥが怪しい。

Ｃをｎとおいてみよう。
Ａ…ｎ－２、Ｅ…ｎ＋２
Ａ×Ｅ＋Ｐ＝Ｃ²
（ｎ－２）（ｎ＋２）＋Ｐ＝ｎ²
ｎ²－４＋Ｐ＝ｎ²
Ｐ＝４
Ｘ…ア、Ｙ…オ、Ｚ…ウ、Ｐ…４（Ｘ・Ｙは順不同）

＠余談＠
具体的な数値を適当にあてはめて検証してもいい。

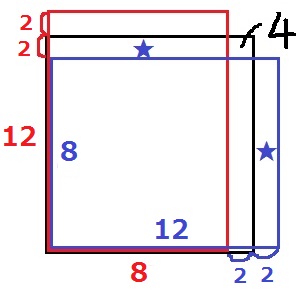
８×12＝96の長方形を10×10＝100にするには＋４する。
ちなみに、連続する７つの整数では、最小値×最大値＋９＝（中央値）²となる。
平方数を足していくことになる。

大問４（数量変化）－30.9％

（１）　65.3％
説明問題。
０≦ｘ≦30のグラフは原点Ｏから（30、2400）を通過する。
傾きは2400÷30＝80
ｙ＝80ｘ
これにｘ＝11を代入して、ｙ＝80×11＝880ｍ
図より家から駅までの距離は900ｍで、880＜900だから家から駅までの間にいる。
ア

（２）　34.7％
希が図書館を出発した時刻がわからないのでＢから決める。

60分後の駅からさかのぼる。
図書館～駅は2400－900＝1500ｍ
これを分速75ｍで歩くから、1500÷75＝20分
希が図書館を出発したのは20分前の９時40分。
Ｂ（40、2400）

姉は2400ｍを分速200ｍで移動するので、2400÷200＝12分
家を出発した時刻は12分前の９時28分。
Ａ（28、０）
Ａ…（28、０）Ｂ…（40、2400）

（３）　10.8％！

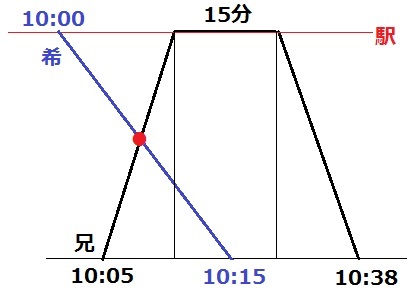
グラフの最後のほうを追記する。
兄は65分後の10時５分に家を出発。
駅で15分間おしゃべりしてから、行きと同じ速さで帰る。
行きと帰りの時間は同じ（図形は等脚台形）
兄が駅までかかる時間は、（10：38－10：05－15分）÷２＝９分

家～駅を希は15分、兄は９分。
時間の比は希：兄＝15：９＝⑤：③

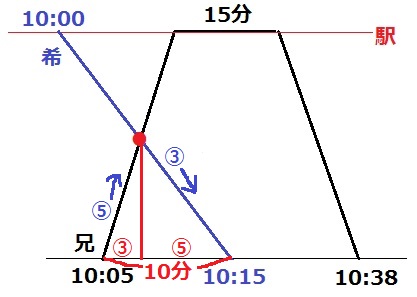
中学受験の戦法を使わせていただきます。
希と兄がすれ違う交点から垂線を下ろす。
この垂線の距離を移動する時間の比は希：兄＝⑤：③
③＝10分×③/⑧＝３・３/４分＝３分45秒
希と兄がすれちがったのは、10時５分から３分45秒後。
10時８分45秒

大問５（平面図形）－29.4％

（１）　42.4％

１つしか変更できないので、『１組の対辺が平行でかつ長さが等しい』を使う。
平行は変わらない。変わったのは上と下の長さ。
符号を入れ替えればいい。
エ：ＡＤ＋ＤＥ＝ＣＢ＋ＢＦ

＠余談＠
私どこかでコレ見かけたことあるな(´ω`).。0
とデジャブにかられて記憶をたどると、３年前の全国学力テスト数学Ｂに酷似してました。

良い問題は記憶に残ります。

（２）　44.9％
△ＤＧＥ≡△ＢＨＦの証明。

仮定より、ＤＥ＝ＢＦ
ＡＥ//ＣＦの錯角より、∠ＧＥＤ＝∠ＨＦＢ（●）
同じく錯角とＡＢ//ＤＣの同位角で、∠ＥＤＧ＝∠ＦＢＨ（×）
１辺と両端角が等しく合同。

（３）　3.6％!!

面積の小さい△ＨＢＦに狙いを定める。
△ＨＢＦ∽△ＨＡＥの相似比は１：４→ＢＨ：ＨＡ＝１：４
△ＨＢＦの面積を【１】とおくと、△ＡＨＦは【４】

△ＡＦＢは【５】
△ＡＦＢ：△ＡＦＣ＝ＦＢ：ＦＣ＝１：４ゆえ、
△ＡＦＣ＝【５】×４＝【20】
平行四辺形ＡＦＣＥ＝△ＡＦＣ×２＝【40】

対角線ＡＣとＥＦで分けると、平行四辺形の面積は４等分される。
△ＯＦＣ＝【40】÷４＝【10】
四角形ＯＨＢＣ＝【10】－【１】＝【９】
したがって、12×【９】/【40】＝27/10ｃｍ²

大問６（空間図形）－19.5％

（１）　65.3％

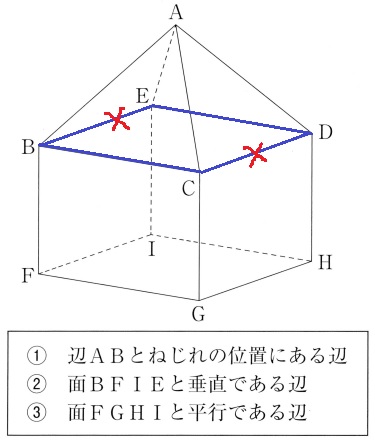
サボは③から考えました。
③底面の面ＦＧＨＩと平行なのは青線の４辺。
②面ＢＦＩＥと垂直なのは辺ＢＣと辺ＤＥ。
①辺ＢＣは辺ＡＢと交わるので辺ＤＥが答え。

＠余談＠

昨年の埼玉でも同じ図形が出ています。
『辺ＢＦとネジレにある辺は何本か』という設問です。
学校選択問題という難関校を目指す生徒たちのなかで正答率が23.1％しかありませんでした。
正解は６本。

（２）　11.1％！

△ＡＫＪ∽△ＡＥＤより、ＫＪ：ＥＤ＝①：③
ＫＪ//ＥＤ//ＦＧより、ＦＧ＝ＥＤ＝③
四角形ＫＦＧＪは台形（正面からみると左右対称の等脚台形）
下底ＦＧ（③）＝６ｃｍだから、上底ＫＪ（①）＝２ｃｍ
ＪＬは台形の高さにあたる。
ＪＫ＝16√５×２÷（２＋６）＝４√５ｃｍ

（３）　0.8％!!!

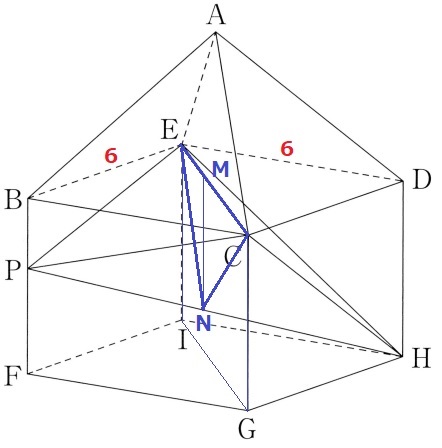
Ｅ・Ｃ・Ｈは直方体の頂点、Ｐだけ変な位置にある。
Ｐ方向から四面体ＰＨＥＣを眺めると、左右対称の立体である。
辺ＰＨと面ＥＩＧＣが交わる点をＮ、Ｎの真上にある面ＢＣＤＥ上の点をＭとする。
正面方向の長方形ＢＦＨＤで切り取るとＣとＥが重なり、図中のＭＮが求められそう。

Ｎの真下（ＩＧとＦＨの交点）をＯとする。
ＰＦ＝ ５－２＝３ｃｍ
△ＰＦＨ∽△ＮＯＨにおいてＯはＦＨの中点だから、
中点連結定理でＮＯ＝３÷２＝1.5ｃｍ
ＭＮ＝５－1.5＝3.5ｃｍ

ＭＮは△ＥＮＣ上の線分であり、辺ＢＦと辺ＤＨは△ＥＮＣと平行。
ＰをＢへ、ＨをＤへ等積変形して立体を変形する。
すると、四面体ＰＨＥＣは正四角錘Ｎ－ＢＣＤＥとなる。
６×６×3.5÷３＝42ｃｍ³