平均44.4点(前年比;-11.4点!)
問題はこちら→リセマムさん
2020長崎B問題の解説は別ページ。
大問1(小問集合)
(1)
6+4×(-2)
=6-8
=-2
(2)
3/5-1/2
=1/10
(3)
3√5-√80
=3√5-4√5
=-√5
(4)
980×110/100(110%)=1078円
(5)
3a+4b<3000
*『より』なので3000円は含まない。
(6)
a(x+y)+2(x+y) ←共通因数は(x+y)
=(x+y)(a+2)
(7)
x2-3x-2=0
解の公式。
x=(3±√17)/2
(9)
無作為に抽出した30個のうち、白は6個。
→全体の1/5が白とみなす。
500×1/5=100個
(10)
垂直二等分線の作図。
①AとBから適当な弧を描く。
②2つの弧の交点を結ぶ。
大問2(小問集合2)
(1)①
6×6=36通り
②
偶×偶=偶、偶×奇=奇、奇×奇=奇
積が奇数となるには、2つとも奇数でなければならない。
奇数は1・3・5だから、3×3=9通り
9/36=1/4
(2)①
80/500=16/100=0.16
*相対度数は小数で表す。
②
最頻値(モード)が120円だから。
*モードは最もあらわれている値。
120円のおにぎりが最も売れている。
(3)
整数の証明。
小さい奇数を2n-1とおくと、大きい奇数は2n+1となる。
(2n+1)2-(2n-1)2 ←平方の差
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2=8n
nは整数だから8nは8の倍数。
したがって、2つの続いた奇数では、
大きい奇数の平方から小さい奇数の平方を引いた差は8の倍数となる。
大問3(関数)
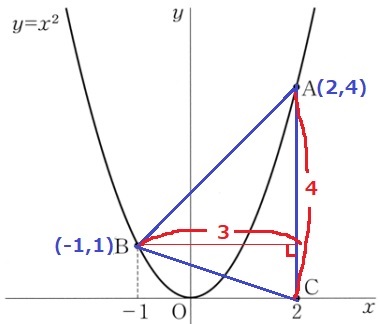
(1)
y=x2にx=-1を放り込んでy=1
(2)
x=-1のとき、y=1
x=2のとき、y=4
変化の割合=yの増加量/xの増加量=(4-1)/{2-(-1)}=1
*y=ax2において、xの値がp→qに増えるときの変化の割合はa(p+q)
1×(-1+2)=1
(4)①
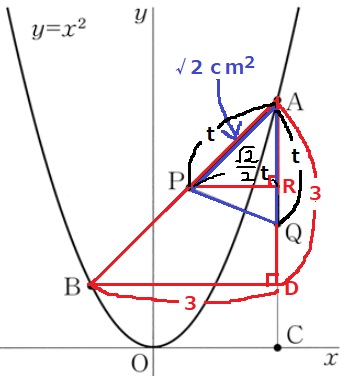
△APQの情報が与えられたので、前問のようにAQを底辺とした高さに見当を付ける。
PからACに垂線をひいてその足をR、Bの足をDとする。
AD=BD=3cmだから、△ABDは直角二等辺三角形。
△ABD∽△APRより、△APRも直角二等辺三角形。
AP:PR=√2:1
PR=t×1/√2=√2/2t
△APQの面積で等式。
t×√2/2t×1/2=√2
√2/4t2=√2
t2=4
t>0から、t=2
②
PR=√2/2t=√2/2×2=√2
Pのx座標はAのx座標2から√2をひく。
2-√2
大問3(空間図形)
(2)
底面積×高さ÷3
6×6×3√6÷3=36√6cm3
(3)
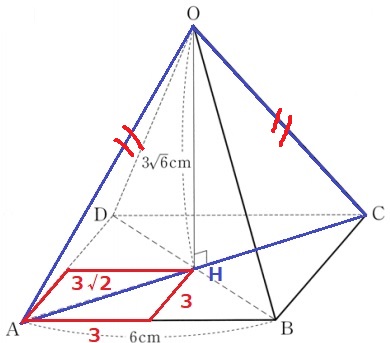
『正四面体OABCD』だからOA=OCは確定。
ACの長さはOA・OCに等しいか。
Oの足をHとする。
赤い正方形は1辺3cmの正方形で、AH=3√2
もし、△AOCが正三角形であれば、∠AOH=30°でなければならない。
すなわち、△AOHの内角は30°-60°-90°の直角三角形となり、
辺の比は1:2:√3でAH:HO=1:√3となる。
AH:HO=3√2:3√6=1:√3
よって、△OACは正三角形。(④)
(4)①
前問の解答を利用する。
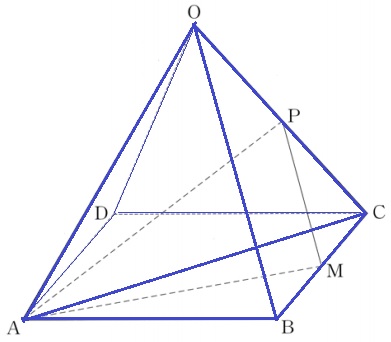
(2)より、正四角錘O-ABCDの体積は36√6cm3であった。
三角錐O-ABCは底面が半分だから体積も半分。
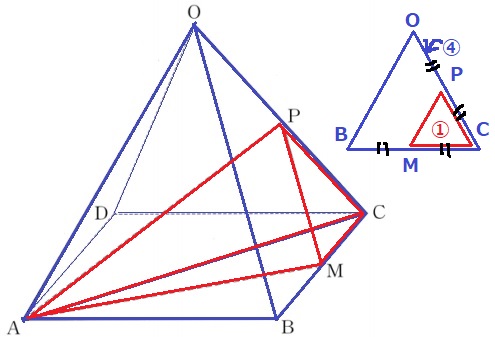
三角錐O-ABCを今度は△OBCを底面として捉える。
△OBC:△PMCの面積比は4:1なので、
三角錐A-OBCと三角錘A-PMCの体積比も4:1。
三角錐A-PMCの体積は、36√6×1/2×1/4=9√6/2cm3
②
体積がわかったので、底面となる△APCの面積を求めたい。

正三角形OACに注目。
AH=3√2cmだったので、AC=6√2cm
OP:PC=1:1で、△OACと△PACの高さの比は2:1
→△PACの面積は正三角形OACの半分。
△PAC…6√2×3√6÷2÷2=9√3cm2
9√6/2×3÷9√3=3√2/2cm
大問5(平面図形)
(1)
△ABEで三平方。
AE=3cm、AB=4cmだから、3:4:5でBE=5cm
(2)①
△AEF∽△CBFの証明。
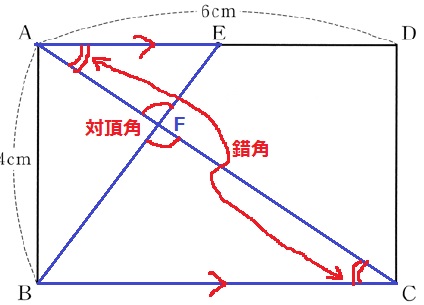
チョウチョウ型の相似。
対頂角+平行線→錯角=2角相等で∽
②
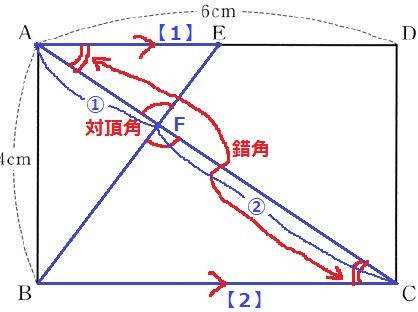
対応する辺の比から、AF:FC=①:②
方針【△ABC→△BCF】
6×4÷2×2/3=8cm2
③
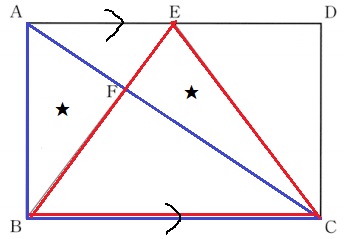
AD//BC→等積変形で△ABCと△EBCの面積が等しい。
2つの三角形から共通する△FBCをひいた部分、
すなわち、△ABFと△CEFの面積も一緒。
④
(3)
ここで空間に移る。

折りたたむと三角錐になる。
△OBC以外(△OBE+△EBC+△OCE)の合計は長方形の面積24cm2
これに△OBCの面積を足せばいい。
△OBCは等辺4cm、底辺6cmの二等辺三角形。
Oの足をHとして、△OBHで三平方→OH=√7cm
△OBC…6×√7÷2=3√7cm2
四角錘O-BCEの表面積は24+3√7cm2
大問6(数量変化)
(2)
桜は2000mを一定の速さで16分間走る。
2000÷16=分速125m
(3)
6分後に注目。
昇は800m地点で休憩をしている。
桜は125×6=750m地点を走っている。
両者の差は800-750=50m
ここから昇は分速100m、桜は分速125mで走るので1分間に25mずつ差が縮まる。
50÷25=2分
桜が昇に追いつくのは6+2=8分後
(4)①

千代のグラフを記入する。
千代は反対方向に走るので右下のライン。
分速100mだから400mを4分で走る(4分後ごとに右下ライン)
交点の★がハイタッチする地点。
昇の4分後は下上に交点ができるがダブルカウントしないこと!
16回
②
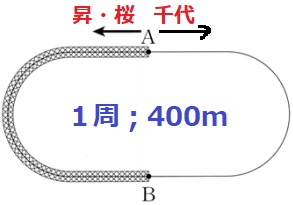
ABは昇&桜が出発する方向の半周にあたる。

ということは、先ほどのグラフの下半分がABの区間に相当する。
★の数は9回。(昇の4分後は下でカウントすること!)
●講評●
大問1
全問死守。
大問2
(1)①整数問題の偶数・奇数判定にも慣れておきたい。
(2)②解答はシンプルに。
大問3
(4)①△APQの面積√2を使うので、その底辺と高さをtで表す。
①が解ければ②はすぐ出せる。
大問4
最も正解率が低そうな予感。
(3)二等辺で安心したらダメだよ!
(4)①視点を変えて立体を捉える。
初手は正四角錘を半分にするのがポイント。
大問5
前半は基本問題。
(3)3つの三角形はバラバラで計算しない。和は長方形の面積となる。
大問6
(1)(2)基本ゆえ必答。
(3)高校受験では方程式を用いるが、算数で解く方が楽。
(4)グラフさえ記入できれば計算は不要であった。
②グラフの下半分が答え。上半分にしないようにする。





コメント