2016年度　千葉県公立高校入試【前期】数学解説

平均４７．４点
問題はコチラから→ＰＤＦファイル

大問１（計算）－77.0％

（１）　97.8％
－１８÷（－３）
＝６　　

（２）　85.8％
－３²＋１６×３/４
＝－９＋１２　
＝３

（３）　52.4％
２ｘ＋３ｙ－(ｘ＋５ｙ)/２       ←方程式の問題ではないので分母を払わない
＝２ｘ－１/２x＋３ｙ－５/２y　←展開するとき＋５ｙにもマイナスがかかる
＝３/２ｘ－１/２ｙ

（４）　74.4％
ｘ＋３．５＝０．５（３ｘ－１）　←１０倍
１０ｘ＋３５＝５（３ｘ－１）
５ｘ＝４０
ｘ＝８

（５）　69.5％
（√２－√５） ²
＝２－２√１０＋５
＝７－２√１０

（６）　82.1％
（ｘ＋２）（ｘ－６）－９　←前半を展開後、因数分解
＝ｘ²－4ｘ－１２－９
＝ｘ²－４ｘ－２１
＝（ｘ－７）（ｘ＋３）
計30点。解の方程式はなかった。

大問２（小問集合）－42.2％

（１）　66.3％
球の体積は、４/３πｒ³　　球の表面積は、４πｒ²
よって、体積は３２/３πｃｍ³、表面積は１６πｃｍ²　→　ウ

（２）　49.４％
最近ブレイク中の統計問題。
10～15の度数が９なので、相対度数は９/２３を小数に変換。
９÷２３＝0.39…　→　0.4

（３）　62.4％
連立方程式。
十の位の数をｘ、一の位の数をｙとおく。
ｘ＋ｙ＝１２　・・（１）
もとの整数は１０ｘ＋ｙなので、入れかえてできる整数は１０ｙ＋ｘ
１０ｘ＋ｙ－１８＝１０ｙ＋ｘ
９ｘ－９ｙ＝１８
ｘ－ｙ＝２　・・（２）
連立で、ｘ＝７　ｙ＝５　　よって、７５。
７５－５７＝１８になりますね。

（４）　29.4％！
扇形内部にある点の数を求めたい。
曲線なのが曲者だが、ありがたいことに図が提供されているので、
格子点を書き、自力で調べる。
３：４：５の直角三角形から、（４、３）（３、４）の点が弧の上にくる。

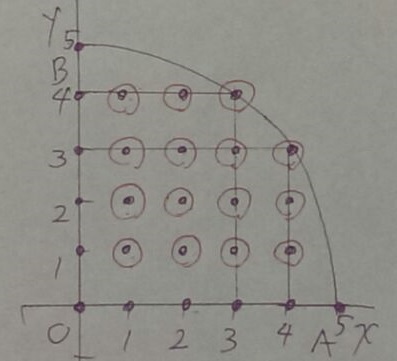
横の行や、縦の列ごとに整理して数える。
０はないので、ｘ軸上とｙ軸上は数えない。
よって、１５/３６＝５/１２

（５）　3.3％!!
辺ＡＣを２：１に内分する点を作図する問題。
シンプルだが慣れていないと難しい。キーワードは相似。
　　
公式解答のやり方は、おそらくこういうことだろう↓

まず、ＡＢの中点Ｄを求める。
Ｄを通るＢＣに平行な線と、Ｃを通るＢＤに平行な線をひき、交点をＥとする。
四角形ＤＢＣＥは２組の辺が平行である平行四辺形。
対辺が等しいのでＤＢ＝ＥＣ。
△ＰＡＢ∽△ＰＣＥ（２角等しい）なので、ＡＢ：ＣＥ＝ＡＰ：ＣＰ＝２：１
よって、点ＰがＡＣを２：１に内分することになる。
問題の三角形から、相似図形を作りださなくてはならないという鬼畜っぷり。

＠書き方＠

ＡＢの中点Ｄは、垂直二等分線。

平行四辺形を書く→Ｅを作りたい。
平行四辺形は２組の対辺が等しい。
そこで、ＢＤの長さをとって、Ｃを起点にヒョコ。
つづいて、ＢＣの長さをとり、Ｄからヒョコ。
交点がＥで、平行四辺形ができる。
歪んでしまった・・(;´Д｀)

ＢＥ（平行四辺形の対角線）をひく。
ＡＣとの交点がＰ。

＠別解＠
線分を自由自在に内分する、とっておきの方法がある。

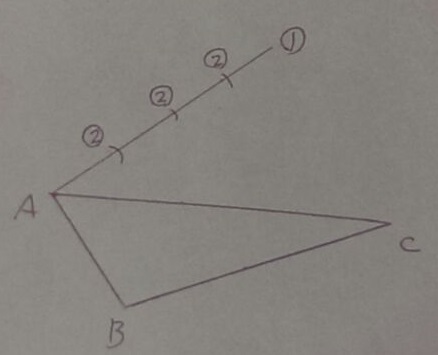
Ａから適当な半直線をかく。
等しい間隔で、３つヒョコヒョコヒョコ。

３つ目のヒョコとＣを結ぶ。
この直線と、２つ目のヒョコを通る平行な線をひく。
すると、三角形と平行線の比から、ＡＰ：ＰＣ＝２：１となる。
上の図で、平行線は角の移動を利用した。

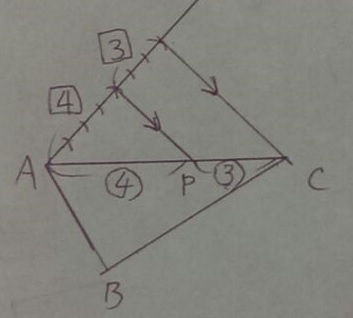
↑丁寧に描ければ、７等分して４：３にも分けられる。

余談だが、日本数学会が実施した「大学生数学基本調査」に関する報告書によると、線分を３等分する作図問題の正答率は、国立Ｓで１３．１％。私立Ｓにいたっては２．３％。大学生全体で４．４％という惨憺（さんたん）たる結果がでている…。
その惨憺たる結果はコチラ↓
http://mathsoc.jp/comm/kyoiku/chousa2011/report6_25.pdf
ＰＤＦファイルです。６ページ目、３「相似を利用した作図」のところ。

大問３（関数）－29.6％

（１）　69.8％

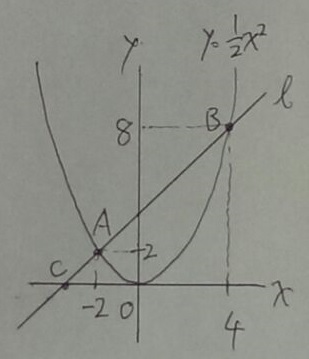
ＡとＢの座標が求まる。Ａ（－２、２）　Ｂ（４、８）
Ａをｘ軸方向に＋６、ｙ軸方向に＋６移動　→Ｂなので、
直線ℓの傾きは１。（４５度）
Ａをｘ軸方向に＋２、ｙ軸方向に＋２　→　切片４
よって、ｙ＝ｘ＋４

（２）【１】　18.1％！
過去問でお馴染み、座標の文字式問題。
Ｐのｘ座標をｔとおく。Ｐ（ｔ、１/２ｔ²）
すると、△ＰＣＤと△ＰＢＤの面積がｔで求められる。

△ＰＣＤの面積×６＝△ＰＢＤの面積で２次方程式。
８×１/２ｔ² ÷２×６＝８×（４－ｔ）÷２
これをｔについて解けば答えがでる。
　
もしくは、底辺がともに８なので、高さだけを抜け出してもＯＫ。
底辺が同じで面積が６倍＝高さが６倍
１/２ｔ²×６＝４－ｔ
３ｔ²＋ｔ－４＝０
解の公式　ｔ＝（－１±√４９）/６＝－４/３、１
問題文から０＜ｔ＜４なので、ｔ＝１　　答え、１

【２】　1.0％!!
回転体ということは丸くなる。
ということは、知りたいところは自ずと限られる。
それは、回転体の半径。

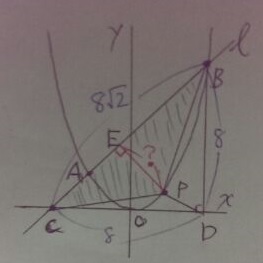
Ｐを通るＢＣに垂直な線をひき、ＢＣとの交点をＥとする。
ＥＰが回転体の半径。
　
ＥＰは上の平面図から求められる。
【△ＢＣＤ－（△ＰＣＤ＋△ＰＢＤ）＝△ＰＢＣ
→△ＢＣＤは１：１：√２から底辺ＢＣがわかる。
→△ＰＢＣ面積×２÷底辺ＢＣ＝高さＥＰ】
　
△ＢＣＤ・・８×８÷２＝３２cm²
△ＰＣＤと△ＰＢＤの和を求める。
底辺はともに８。△ＰＣＤの高さ１/２。△ＰＢＤの高さは１/２×６＝３
△ＰＣＤ＋△ＰＢＤ（１/２＋３）×８÷２＝１４cm²
△ＰＢＣ＝３２－１４＝１８cm²
ＢＣは△ＢＣＤが１：１：√２から、８√２cm
ＥＰ＝１８×２÷８√２＝９√２/４
回転体の体積は、９√２/４×９√２/４×π×８√２÷３＝２７√２πｃｍ ³

大問４（平面図形）－43.6％

（１）図形の証明問題。
そんなに難しくはないので取りたい。
　
図形が円に囲まれている→円周角の定理
（ａ）直径ＤＦから９０度となる角を探す。→∠ＤＥＦ：イ　83.1％
（ｂ）∠ＤＣＡと∠ＤＥＦの位置関係。　→同位角：カ　　　 81.3％
　
（ｃ）６点―8.2％！　３点―2.9％　無答―59.4％！
辺の情報が乏しい→角度から攻める。
どの角が等しくなるかを考える。
円周角の定理を用いるので、弧に注目する！

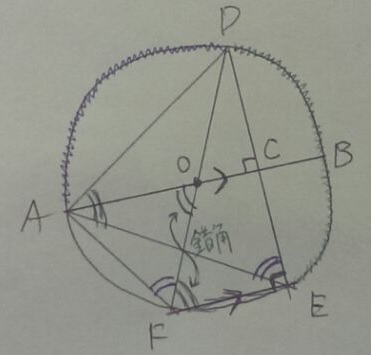
イガグリみたいなのは、対応する弧。
弧ＤＥに対する円周角が緑。
弧ＡＤに対する円周角が青。
錯角のコンボで、２角が等しくなる。
 
－公式解答引用－
【４】より、平行線の錯角は等しいので、
∠ＡＯＦ＝∠ＤＦＥ　・・【５】
弧ＤＥに対する円周角は等しいから、
∠ＤＦＥ＝∠ＤＡＥ　・・【６】
【５】【６】より、∠ＡＯＦ＝∠ＤＡＥ　・・【７】
弧ＡＤに対する円周角は等しいから、
∠ＡＦＯ＝∠ＤＥＡ　・・【８】
【７】【８】より、２組の角がそれぞれ等しいので、
△ＡＯＦ∽△ＤＡＥ
－引用おわり－

（２）　1.9％!!!
いつも通り、悩む。
（１）の相似ではなく、平行線を利用する。

△ＡＥＦは変な場所にあるので、等積変形で△ＣＥＦへ移動。
∠ＣＥＦ＝９０°
直角三角形ＤＥＦは、半径からＤＯ＝ＯＦ。
また、ＯＣ//ＦＥなので、三角形と平行線の比から、ＤＣ：ＣＥ＝１：１
求められそうな気がする。
ＤＣとＯＣの長さがわかれば、いろいろわかりそう。
△ＤＡＢは、１０：８：６＝５：４：３の直角三角形。
△ＤＡＢと△ＣＤＢは２角が等しいので相似（５：４：３）
ここに気づけるかどうかが勝負の分かれ目。
直角三角形は相似の宝庫。直角三角形の内部に直角三角形があれば相似を疑おう！
ＤＣ＝６×４/５＝２４/５
ＣＢ＝６×３/５＝１８/５
ＯＣ＝ＯＢ－ＣＢ＝５－１８/５＝７/５

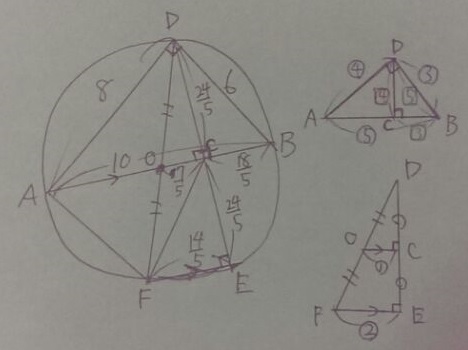
△ＤＯＣ∽△ＤＦＥに注目。
辺の比は１：２。
ＣＥ＝ＤＣ＝２４/５
ＦＥ＝ＯＣ×２＝７/５×２＝１４/５
よって、１４/５×２４/５÷２＝１６８/５ｃｍ²
直角三角形の相似。地味だけど、使いこなせれば応用範囲が広がります。

大問５（規則）－40.6％

（１）　89.0％
整数の倍数に関する規則。
Aは２の倍数、Bは３の倍数、Cは４の倍数、Ｄは５の倍数、Ｅは６の倍数でつく。
１０は２の倍数と５の倍数。よって、ＡとＤがつく。（完答）
表に４回足して調べてもできる。

（２）（ａ）　57.5％
次にＡ～Ｅすべてが点灯するときは、Ａ～Ｅの全ての倍数。
つまり２、３、４、５、６の最小公倍数。
よって、６０回。

（ｂ）　13.0％！
６０回までにＡ～Ｅすべてが点灯していない回数は何回あるか。
点灯しない規則は難しいので、全体から、少なくとも１個は点灯している回数をひく。
　
倍数の規則に着目をする。
４と６の倍数は２の倍数である。
言い換えれば、ＣかＥが点灯するときは、必ずＡも点灯する。
６の倍数は３の倍数でもある。
言い換えれば、Ｅが点灯するときは、必ずＡとＢも点灯する。
↑ここに気づくこと。
つまり、少なくとも１個は点灯している回数は、
”２の倍数or３の倍数or５の倍数”だけを考えればいい。
あとはベン図の処理。問題集で解きなれていないと落とす。
２の倍数or３の倍数or５の倍数
＝２の倍数＋３の倍数＋５の倍数－６の倍数－１０の倍数－１５の倍数＋３０の倍数
＝３０個＋２０個＋１２個－１０個－６個－４個＋２個＝６２－２０＋２＝４４個
ベン図は重なっているところが重複しますからね！３個重複する真ん中は足し算。
全てが点灯していない回数＝２の倍数でも３の倍数でも５の倍数でもないのは、
６０－４４＝１６回

（３）　3.0％!!
「電球の位置にある点を結んでできる図形が、正五角形の１つの辺と２つの対角線からなる三角形になる」
こういうことです↓

各辺の両端と、各辺の反対側にある頂点を結んだ三角形です。
１辺に１パターン。５辺なのでパターンは５つ。
これら３つだけが点灯している状態を数える。

ここで、さっきの規則を思い出す。
４と６の倍数は２の倍数である。
言い換えれば、ＣかＥが点灯するときは、必ずＡも点灯する。
６の倍数は３の倍数でもある。
言い換えれば、Ｅが点灯するときは、必ずＡとＢも点灯する。
Ｅがつく→ＡとＢもつく！
Ｃがつく→Ａもつく！

３つしか点灯してはいけないので、４つ以上点灯するものを除外。
ＡＢＤ→ありうる。
ＢＣＥ→ＥによってＡもつく。×
ＡＣＤ→ありうる。
ＢＤＥ→ＥによってＡもつく。×
ＣＡＥ→ＡによってＢもつく。×

・ＡＢＤが点灯している状態
２の倍数と３の倍数と５の倍数なので、３つ点灯するのは３０の倍数。
しかし、３０の倍数は６の倍数でもあるので、Ｅも点灯する→４つ点灯→×

・ＡＣＤが点灯している状態
２の倍数と４の倍数と５の倍数なので、３つ点灯するのは２０の倍数。
ここから、ＢかＥも点灯している回数をひく。
Ｂは３の倍数、Ｅは６の倍数なので、
ＢがつけばＥもつくから、点灯回数の多いＢだけを考える。
２０（ＡＣＤ）と３（Ｂ）の最小公倍数は６０。
２０の倍数でも６０の倍数（Ｂの点灯…というか全点灯）を除く。
２０５までに倍数が何個あるかを計算。
２０の倍数の個数－６０の倍数の個数＝１０個－３個＝７個
よって、ＡＣＤだけが点灯している状態は７回となる。
公立高校入試解説ページに戻る