問題はこちら→東進ハイスクールさん(解答)
出題範囲の除外は標本調査。
大問1(小問集合)
(1) 94.2%
-3-(-7)
=-3+7
=4
(2) 94.3%
8a3b5÷4a2b3
=2ab2
(3) 89.4%
a+b2
=2+(-3)2
=2+9=11
(4) 82.6%
x2-8x+16
=(x-4)2
(5) 63.1%
a=(2b-c)/5 ←5倍
5a=2b-c
c=-5a+2b
(6) 49.6%
ア:2乗してaになる数をaの平行根という。9の平方根は±3〇
イ:√16は正の数だから、√16=4×
ウ:√5+√7≠√12×
エ:(√2+√6)2=8+4√3、(√2)2+(√6)2=8×
ア
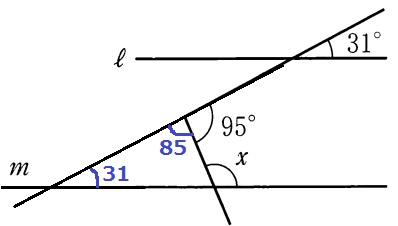
(7) 73.9%
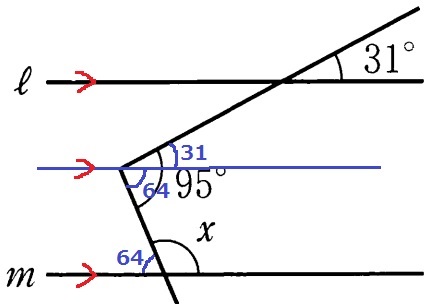
3本目の平行線をひき、同位角や錯角でおろしていく。
x=180-64=116°
(8) 74.1%
反比例の比例定数aは積xyで一定。
a=3×6=18
y=18/x
(9) 67.1%
6×6×6÷3=72cm3
(10) 79.5%
x2+5x+2=0
解の公式を適用。
x=(-5±√17)/2
(11) 59.8%
傾きaが負なので、グラフは右下。
x=-1のとき、最大値y=-2×(-1)+1=3
x=3のとき、最小値y=-2×3+1=-5
-5≦y≦3
(12) 29.6%!
『20分以内でBに到着』だから、時間で不等式を立てる。
歩いた時間はa/60分、走った時間はb/100分。
a/60+b/100≦20
(13) 85.7%
AB:DE=AC:DF
5:4=2:x
x=4×2/5=8/5cm
(14) 53.0%

菱形を想起する。
AB=BC、AC⊥BD、∠ABD=∠BCDは菱形(または正方形)の場合。
長方形は4角が直角で等しいほか、対角線の長さが等しい。
ウ
大問2(小問集合2)
(2) 61.0%
a-bが正の数になる→a>b
aが6のときbは5通り、aが5のときbは4通り、aが4のときbは3通り…
5+4+3+2+1=15通り
確率は、15/36=5/12
(3)① 9.8%!(部分正答含41.6%)
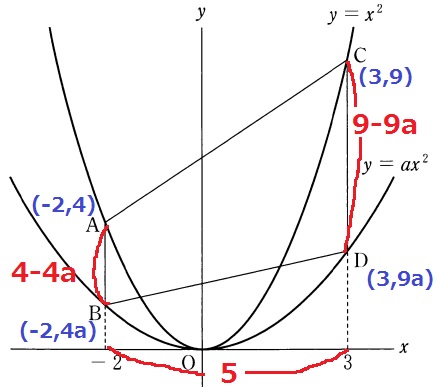
まずは座標を確定する。
AB=4-4a
②
四角形ABDCは上底が4-4a、下底が9-9a、高さが5の台形である。
{(4-4a)+(9-9a)}×5÷2=26
13(1-a)×5/2=26 ←÷13
(1-a)×5/2=2
1-a=4/5
a=1/5
大問3(方程式・データの活用)
(1) 42.8%(部分正答含65.0%)
答案では途中式も記述する。
大きい袋がx個、小さい袋がy個。
合わせて40個だから、x+y=40 …①
2つ目の式はりんごの個数で等式を立てる。
5x+3y+57=7x+4y
2x+y=57…②
②-①で、x=17
①に代入。y=40-17=23
大きい袋…17枚、小さい袋…23枚
(2)① 64.1%
最頻値(モード)は最もあらわれている値。
12分
② 70.6%
5分以上10分未満の度数は6人。
相対度数は、6÷15=0.4
③ 1.7%!!(部分正答含12.2%)
推論問題。

範囲は変わらないので、最小値3と最大値20はいじらない。
15人の中央値は8番目の11分。
これが変わらないということは、11の前から11を超えないように変動する。
5+5=10分
12+5=17分
14+5=19分
最大値20を超えてはならない。
10分、17分、19分
大問4(平面図形)
(1) 12.4%!(部分正答含59.3%)
△DGE≡△FGCの証明。

BC=②、CF=①とする。
△ABCで中点連結定理を適用。
DE//BC、DE=②÷2=①=CF
錯角で2角が等しい。
1辺と両端角が等しいので合同。
(2)① 47.1%
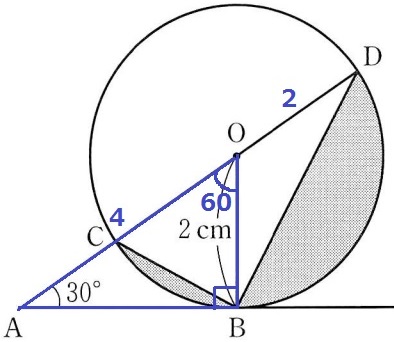
直角三角形OABの内角から辺の比は1:2:√3→AO=4cm
半径OD=OB=2cm
AD=4+2=6cm
② 9.8%!
半円から△BCDをひけばいい。
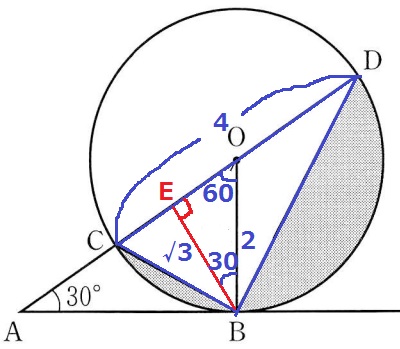
BからCOに向けて垂線、交点をEとする。
△OBEの内角は30°-60°-90°で辺の比は1:2:√3→EB=√3
△BCDは底辺が4cm、高さが√3cm
2×2×π×1/2-4×√3÷2
=2π-2√3cm2
大問5(数量変化)
(1) 63.3%
3×6÷2=9cm2
(2) 26.2%!(部分正答含45.1%)
答案では過程も記述する。
(10、15)→(20、0)
右に10、下に15なので、傾きは-15/10=-3/2
y=-3/2x+b
(x、y)=(20、0)を代入。
0=-3/2×20+b
b=30
y=-3/2x+30
@余談@
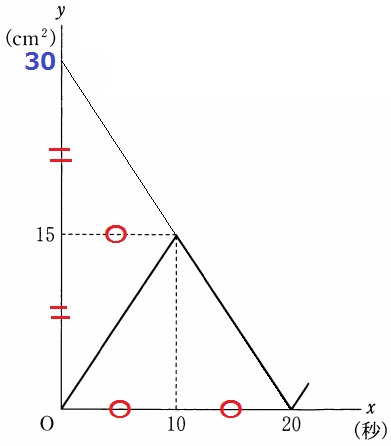
幾何で考えると、切片は15×2=30とすぐ出せる。
(3) 0.4%!!!
図2のグラフの右側がやけに空いているので、そこに付け足す。

四角形BCSRがはじめて15cm2となるのは、RがAB(SがDC)の中点にきたとき。
Pが出発してから、10+5÷0.5=20秒後
30秒後に四角形BCSRは0cm2、40秒後に15cm2となる。
赤い交点が△APQと四角形BCSRの面積が等しくなるときで、
2つのグラフの変化の割合から中点で交わる。
Rは片道20秒、往復で40秒かかるから、
四角形BCSRが再び0cm2となるのは30+40=70秒後
その5秒手前である65秒後が3回目の交点。
t=65
大問6(整数)
(1)Ⅰ 75.9%(部分正答含91.0%)
各シートの最大数は4・8・12…と4の倍数である。
7枚目の最大数…4×7=28
Ⅱ
1枚目の最大数は76。
76から1を足していく。
足される回数は間の数であることに注意!
76+(7-1)=82
(2) 6.0%!!(部分正答含25.9%)
答案では求める過程も記述する。
最も小さいaをxとおく。
a=x、b=x+25、c=x+50、d=x+75
a+2b+3c+4d=ac
x+2(x+25)+3(x+50)+4(x+75)=x(x+50)
10x+500=x2+50x
x2+40x-500
=(x+50)(x-10)=0
x>0から、x=10
(3)① 0.3%!!!(部分正答含3.3%)

nは前問のように考えればいい。
mは〇枚目と〇×4が符号するのが最大数なので、
右下を4mと定めてから、残りのマスを引き算で埋める。
(4m-3)+(4m-2)+(4m-1)+4m=16m-6
n+(n+25)+(n+50)+(n+75)=4n+150
16m-6=4n+150
n=4m-39
②
n=4m-39(0<m<n≦25)
いろんな攻め方があると思われる。
-39の部分を除外して考えると、mが1増えるとnは4増えていく。
試しに最大数25をnに代入すると、
25=4m-39
m=16で整数になっちゃった(;’∀’)
ここからmを-1、nを-4ずつ減らしていくと、
(m、n)=(16、25)(15、21)(14、17)(13、13)…
(13、13)はm<nの条件に反するので×!
n=17、21、25
@別解@
仮にmとnが同数である場合を考えると、
n=4n-39
n=13
ちょうど整数なので、(m、n)=(13、13)のときから、
mを+1、nを+4してnが25以下の範囲を調べる。
●講評●
大問1
(6)平方根の意味と、根号を使わないで表すの違いに注意!
(14)図形の性質を正確におさえておく。イメージも大切。
大問2
(1)基本レベルだが、正答率が34.1%であった。
大問3
(2)③範囲と中央値を崩さないように値を変える。
大問4
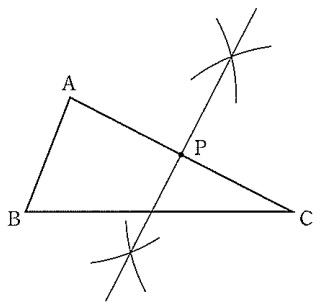
(2)①接線がきたら、半径の作図!
②正三角形を真っ二つにした高さの利用。他県でも登場する。
大問5
(3)いろんなやり方があると思われるが、解説ではグラフの作成を試みた。
周期性のある形になるが、変化の仕方を注意深く見極める必要があった。
大問6
(3)①mは右下、nは左上を起点に文字で表す。
②変化の割合をとらえると、mが1増えるとnが4増える。
関数の考えを整数問題で応用すると、調査が楽になる。



コメント