平均51.5点(前年比;-7.8点)

問題はこちら→千葉日報さん
*形式が大きく変更しています。
大問1(小問集合)-60.8%
(1)① 96.6%
-2×3+2
=-6+2
=-4
② 88.9%
6(2/3a-3/2b)-(a-3b)
=4a-9b-a+3b
=3a-6b
③ 75.2%
(2√3-1)2
=12-4√3+1
=13-4√3
(2)① 62.5%
横がxcm、縦が2x+3cmなので、
長方形の面積はx(2x+3)cm2
② 17.9%!
x(2x+3)=7
2x2+3x-7=0
解の公式を適用。
x>0より、x=(-3+√65)/4cm
(3)① 74.1%
値を昇順に並べ替えると、〔3・7・7・9・11・12・14・16〕
8個の中央値(メジアン)は4番目と5番目の平均で10回。
② 19.1%!
高校から降りてきた箱ひげ図が登場。

中央値(第2四分位数;Q2)が10回→9回に減っている。
9個の中央値は5番目。a>9だと中央値は9回を超えてしまう。
→aは9以下
第1四分位数(Q1)は下位4個の真ん中、下から2番目と3番目の平均で7回。
a=6だとQ1は6.5回になってしまう。×
7≦a≦9だから、a=7、8、9
(4)① 49.3%
素数とは、1と自分自身以外に約数をもたない数。(ただし1を除く)
【2・3・5・7・11・13・17・19】の8個。
② 60.3%
素数なので地道にあてはめるしかない。
●2a+b=2
無い。
●2a+b=3
(a、b)=(1、1)
●2a+b=5
(2、1)(1、3)
●2a+b=7
(3、1)(2、3)(1、5)
●2a+b=11
(5、1)(4、3)(3、5)
●2a+b=13
(6、1)(5、3)(4、5)
●2a+b=17
(6、5)
計13通り
全体は6×6=36通りだから、確率は13/36
(5)a…74.1%、b…67.1%
x=1、y=-1を代入すると、
-a-3=2 …①
2b-a=-1 …②
①より、a=-5
これを②に代入して、b=-3
a=-5、b=-3
② 51.4%
前問の式に代入すればいい。
底面積である正方形ABCDは、4×4÷2=8cm2
h=3×32/3÷8=4cm
(7) 48.2%
作図問題。

方針は立てやすい。
①ACの垂直二等分線でACの中点を見つける。
②これとBを結ぶ。この線上のどこかにPがある。
③AP⊥BPということは、Aを通る垂線と②の交点がPとなる。
大問2(関数)-47.6%
(1) 76.1%
B(5、-15)をy=ax2に代入する。
-15=25a
a=-3/5
(2) 65.1%
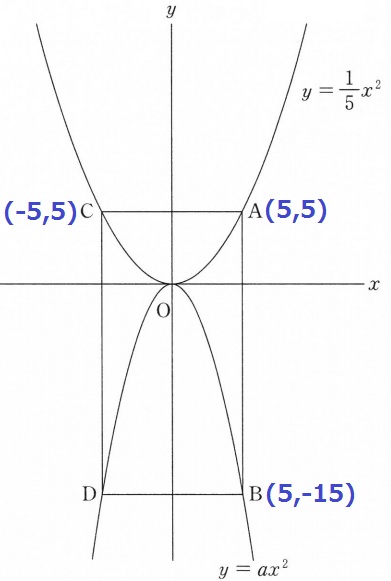
y=1/5x2にx=5を代入して、A(5、5)
y軸についてAを対称移動してC(-5、5)
C(-5、5)⇒B(5、-15)
右に10、下に20だから、傾きは-20/10=-2
Cから右に5、下に10移動して、切片は5-10=-5
y=-2x-5
(3) 1.5%!!
艱難辛苦(ヾノ・ω・`)
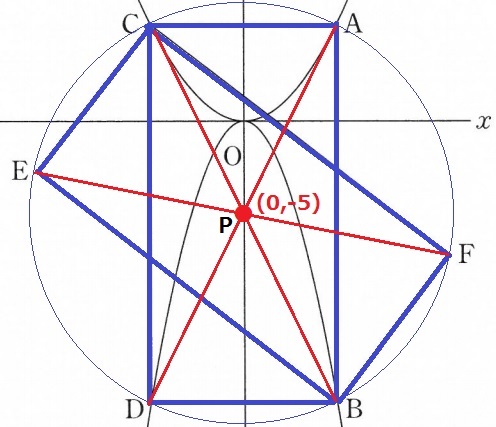
対角線の交点をPとする。
Pは長方形の重心にあたり、対角線BCの中点だからP(0、-5)
(*前問の式の切片にあたる)
頂点はすべてPCを半径とする同一円周上にある。
つまり、長方形CEBFは回転の中心をPとして長方形ACDBを回転移動させた図形。
対角線EFの切片も-5である。

設定がシンプルゆえ、使える情報といえば長方形の長さくらいしかない。
そのなかで特に気になるのがナナメの10(CE)と20(EB)

中学数学の奥義は三平方と相似。
長方形CEBFを大きな長方形で囲うと見えてくるんじゃないでしょうか。
●+×=90°の角度調査で、CEとEBを斜辺とする△CEGと△EBHは2角相等で∽!
GC=xとすると、HB=x+10
相似比はCE:EB=10:20=1:2なので、EH=2x
△EBHで三平方。
(2x)2+(x+10)2=202
4x2+x2+20x+100=400
5x2+20x-300=0 ←÷5
x2+4x-60
=(x+10)(x-6)=0
xは長さなのでx>0より、x=6

GC=6、EH=6×2=12
GE=20-12=8
C(-5、5)から左に6、下に8移動してE(-11、-3)
EからPまでは右に11、下に2だから、傾きは-2/11。
EFはy=-2/11x-5
@別解@
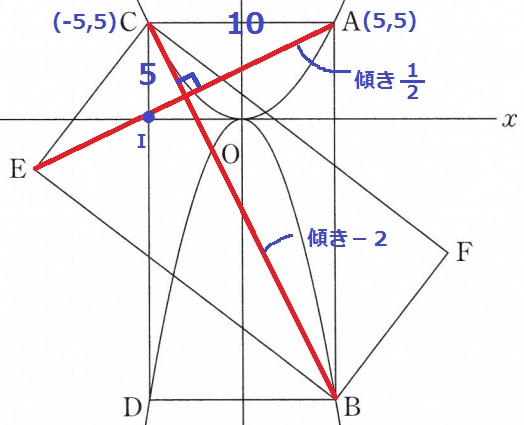
△ABCと△EBCは合同な長方形の半分で合同だから、
BCを対称の軸とするとAとEは対称の点にある。
ということは、AEとBCは垂直に交わっている。
BCの傾きは-2
直交する2直線の傾きの積は-1なので、AEの傾きは1/2
CDとx軸の交点をIとする。
CA=10、CI=5でIAの傾きも1/2だから、IはAE上の点である。
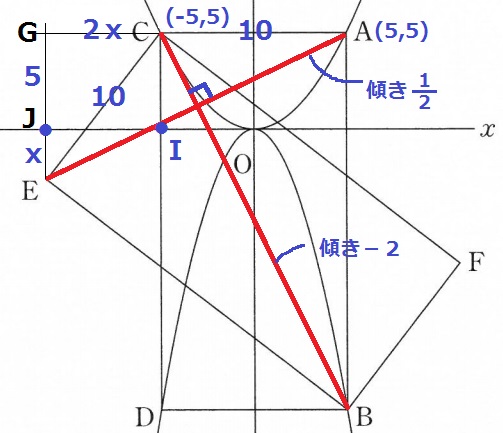
GEとx軸の交点をJとする。
JE=xとすると、傾きからJI=GC=2x
GJ=CI=5
△GCEで三平方。
(2x)2+(x+5)2=102
5x2+10x-75=0 ←÷5
x2+2x-15
=(x+5)(x-3)=0
x>0だから、x=3
EはCから左に6、下に8の点だとわかります。
大問3(平面図形)-37.4%
(1) 78.6%
AIとDHを1辺とする三角形の合同を証明すればいい。
a…ア、b…エ、c…合同
(2)6点―28.2%!、3点―8.3%、無答―27.4%
AI=DHの証明。
まず、前問で示した△AEI≡△DEHを指摘する。

仮定より、AE=DE
対頂角で、∠AEI=∠DEH
AC//FDの錯角で、∠IAE=∠HDE
1辺と両端角が等しいので、△AEI≡△DEH
対応する辺は等しいから、AI=DH
(3) 5.5%!!

△AEIの1辺で最も短いEIを①とする。
△AEI∽△ADCより、DC=②
仮定から、BD=②×3=⑥
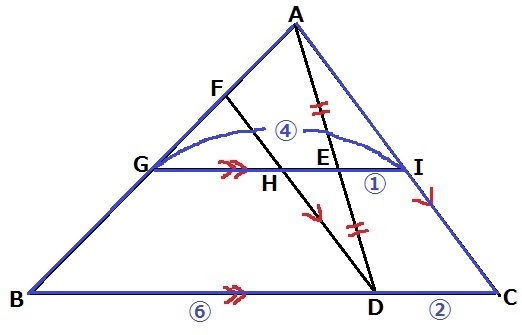
△AGI∽△ABCより、GI=⑧÷2=④
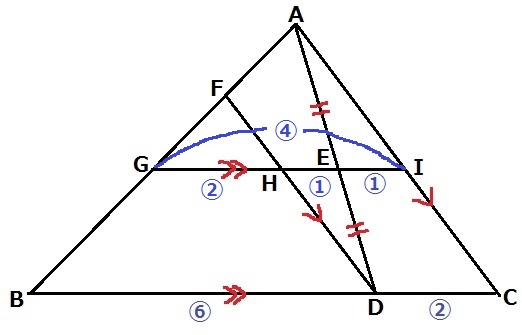
先ほどの合同から、HE=IE=①
GH=④-①-①=②
△AEIと四角形BDHGはAE=EDより高さの比が同じ→高さ共通。
すなわち、底辺の比が面積比になる。
△AEI:四角形BDHG=①:②+⑥(上底+下底)=1:8
@余談@
四角形DCIHは2組の対辺が平行だから平行四辺形。
HI=DC=②からもGH=④-②=②が導ける。
大問4(数量変化)-33.8%
(1)a…86.5%、b…57.1%
QがはじめてCに到着するのは、90÷9=10秒後
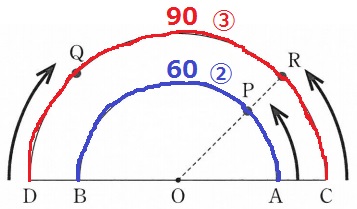
弧ABと弧CDの距離の比は60:90=②:③
距離が3/2倍長くなる。
インコースと同じ時間でアウトコースを回るには速さを3/2倍する。
(*時間一定の場合、距離の比=速さの比)
4×3/2=秒速6cm
a…エ、b…イ
(2) 28.9%!

Qは10秒で片道を行く。0≦x≦30の指定に注意!
(3) 17.5%!

QとRが重なるとき、O・P・Qは一直線上に並ぶ。
QとRは90cm離れ、1秒あたり9+6=15cmずつ近づいていくから、
90÷15=6秒後
(4) 8.1%!!
Pは往復30秒、Qは往復20秒。
最小公倍数の60秒ごとにPとQはスタート地点へ同時に戻る。
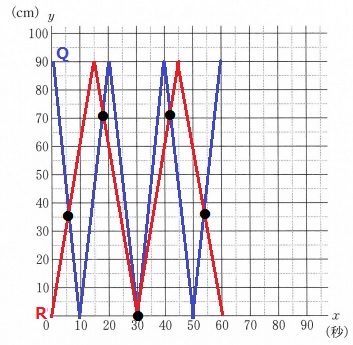
先ほどのグラフで、Pをアウトコースに移動させたRを描く。
QとRが重なった地点で一直線に並ぶので、交点を数えると5回。
(5) 4.4%!!
7年前の大問5で類題が出ている。
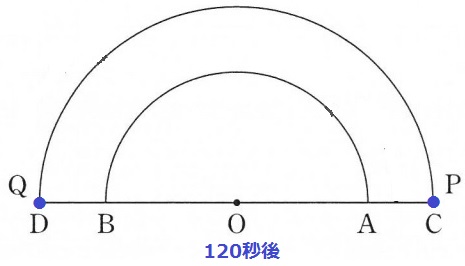
60の倍数ごとで初期状態に戻るので120秒後から考える。
ここから残りの24秒を進める。
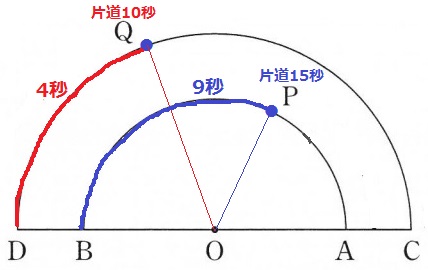
Qは片道10秒だからDから4秒、Pは片道15秒だからBから9秒進んだところ。
おのおの片道の時間で180°進むので、
∠QOD=180×4/10=72°
∠POD=180×9/15=108°
∠POQ=108-72=36°
@別解@

見にくいですけど…グラフから20秒後のQとRは30cm離れている。
20~30秒後の10秒間で差が0になる。
30秒後から6秒手前の24秒後では、30×6/10=18cm離れている。
弧QR=18cm、弧CD=90cmなので、180×18/90=36°
●講評●
大問1
形式が大きく様変わりしている。配点51点
(1)純粋な計算問題は3題に減少。
(2)①横がxなので、縦をxで示す。
(3)②箱ひげ図や四分位数は今後も狙われる。
(5)連立だがaがすぐ求まる。
(6)②展開図はそんなに使わない。
(7)AP⊥BPで、Pの位置は不明だが直線BPは描かれている。
あとは点Aと直線BPの垂線を作図すればいい。
大問2
(3)本試験最大の難所。
Eの座標が知りたいので、CEとEBに着目する。
これらを斜辺とする直角三角形を外側に作成。
もしくは、CBが長方形の対角線であることからAとEが対称関係にある。
⇒AEを結び、CBと垂直の関係にあることを見抜けるか。
難易度が高く、間違えてもあまり差はつかないと思うが、センスの良い問題であった。
大問3
(3)AE=EDから、GIを境に上と下の世界は高さ共通。
底辺の比で決着がつく。台形の場合は上底+下底の比。
大問4
難易度は高くないが、苦手意識があるとツライ。
(1)イ:到着時間が同じで距離が3/2倍だから速さも3/2倍。
(2)グラフの右側はスカスカになる。
(4)出会った回数はグラフの活用。他県でも見かける形式。
(5)24秒後の様子を図示できるか。処理も複雑ではなかった。
@2022年度千葉解説@
社会…平均56.3点 理科…平均52.7点 英語…平均58.7点 国語…平均47.7点
思考力を問う問題…数英国の3教科。来年度は千葉・千葉東・東葛飾が対象。


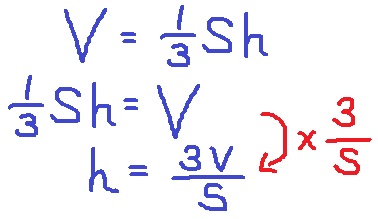

コメント
第2問(3)の別解
直線ABと直線CFの交点をP(5,-p)とおく.
△ACPと△FBPは二角挟辺合同ゆえ△ACP≡△FBP.
従ってAP=FP=5+p.
三平方の定理より
{-15-(-p)}^2=(10^2)+(5+p)^2
これを解いて,p=5/2
これより,直線CPの式はy=(-3/4)x+(5/4)
またCPの長さは20-(15/2)=25/2より,
CF:CP=20:(25/2)=40:25=8:5である.
ゆえEのx座標は,10×(8/5)-5=11,y座標は5-(15/2)×(8/5)=-7
これらをy=mx-5に代入すると,
m=-2/11
よって、求める式は
y=(-2/11)x-5(答)
千葉県印旛地区で塾講師をしているものです。
手のつけようがなさそうに見えて、気付くとスパッと解けました。
コメントありがとうございます。
新しい着眼点を得て勉強になりました。
条件がシンプルなので解法の余地があまりないと思っていたのですが、
1人だとなかなか気づけないものですね(^^;
はじめまして。私はこの間受験が終わった公立中学校の3年生です。私は塾に行かずに勉強していたので、サボ先生の過去問解説がとてつもなく分かりやすく、頼りにしていました。そのおかげで、第1志望であった千葉東高校に合格することが出来ました。本当にありがとうございました。いきなり失礼致しました。
こちらこそ初めましてです。
通塾なしで千葉東は凄い!aさんの努力の賜物ですが、
そういってくださるとブログやって良かったと心底痛感します。
コメントありがとうございました。
高校生活を楽しんで、どんどん羽ばたいてください(*´ω`)
応援しています。 サボ
返信ありがとうございます!
何度もお世話になりました。
充実した高校生活を送れるようがんばります。
本当にありがとうございました。