平均55.2点
問題はコチラ→ＰＤＦファイル
一般の問題は別ページ。
大問１（小問集合）
（１） 85.7％
１/２（３ｘ－ｙ）－（４ｘ－ｙ）/３
＝（９ｘ－３ｙ－８ｘ＋２ｙ）/６
＝（ｘ－ｙ）/６
（２） 45.6％
整理してから代入する。
＠別解＠
ｘ＋ｙ＝（２＋√３）＋（２－√３）＝４
ｘｙ＝（２＋√３）（２－√３）＝１
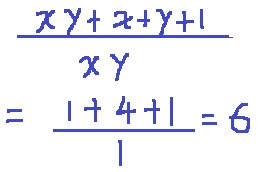
先にｘとｙの和と積を求めてから代入する方法です。
ｘとｙを入れ替えても同じになる対称式とよばれるもので、高校数学で習います。
（３） 76.6％
２（ｘ－２）2－３（ｘ－２）＋１ ←（ｘ－２）をＸと置き換え
＝２Ｘ2－３Ｘ＋１
＝（２Ｘ－１）（Ｘ－１） ←戻す
＝｛２（ｘ－２）－１｝｛（ｘ－２）－１｝
＝（２ｘ－５）（ｘ－３）＝０
ｘ＝５/２、３
（４） 77.2％
ｘ＝３、ｙ＝－４を代入。
３ａ－４ｂ＝11 …①
３ａ＋４ｂ＝－２ …②
①＋②
６ａ＝９
ａ＝３/２
①に代入。
３×３/２－４ｂ＝11
４ｂ＝－13/２
ｂ＝－13/８
ａ＝３/２、ｂ＝－13/８
（５） 64.1％
ａをｂで割ると、商が１/３以上３以下となる。
最も大きい商から６÷１＝６×…６÷２＝３〇
最も小さい商から１÷６＝１/６×…２÷６＝１/３〇
６から調べると２が出た時点で範囲内に収まるので、
起こり得ない場合の数の方が少ないように思える。
そこで、全体から起こり得ない場合を引く。
◆商が３よりも大きい
４÷１、５÷１、６÷１
◆商が１/３未満
１÷４、１÷５、１÷６
以上、６通り。
商が１/３以上３以下は30通り。
30/36＝５/６
（６） 77.5％
反比例の特徴。
ア：反比例はｘとｙの積が比例定数ａになる。２×３＝６〇
イ：点対称→上下さかさまにしても同じ形〇 （双曲線という）
ウ：変化の割合＝ｙの増加量/ｘの増加量。反比例の変化の割合はバラバラ×
エ：反比例はｘが増えるとｙが減り、ｘが減るとｙが増える。
これはｘが正であっても負であっても同じことがいえる。〇
正解→ウ
（７） 73.6％
母線の長さは３：４：５より５ｃｍ。
側面積の扇形の中心角は〔×半径/母線〕で対処しよう。
３×３×π＋５×５×π×３/５＝24πｃｍ2
（８） 60.5％
昇順に並べると〔５・６・７・８・８・９・10〕
この７人の中央値は８。
８人の中央値は４人目と５人目の平均値なので、
Ｈが８未満だと中央値は7.5、Ｈが８以上だと８になる。
７人の合計は53回。
平均値が7.5であれば、Ｈの値は7.5×８－53＝７回
平均値が８であれば、Ｈの値は８×８－53＝11回…10回overなので×
よって、Ｈは７回。
（９） 69.5％（一部正答28.0％）
標本（サンプル）は偏りがないよう、母集団から無作為（ランダム）に選ぶ。
ウ・エは『図書室の利用回数の多い順』と特色をつけて選んでいるので×。
調べたいテーマは全校生徒600人なので、３年生に絞っているアも×。
ランダムで選ぶ際に通し番号を付すのはＯＫ→イ
大問２（平面図形）
（１） 73.3％
接線の作図。
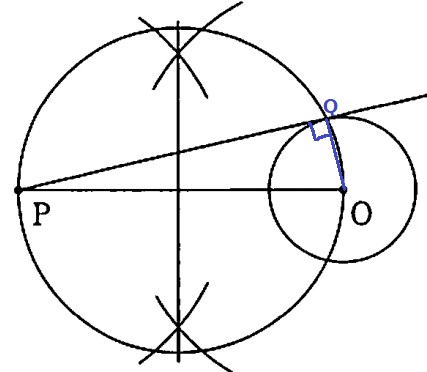
接線と半径は垂直で交わる。
ＰＯを直径とする円を描き、円Ｏとの交点をＱとする。
円周角定理により∠ＰＱＯ＝90°となり、接線と半径が直交する。
①ＰＯを結び、垂直二等分線。
②ＰＯの中点からグルっと円を描く。
③円Ｏとの交点とＰを結ぶ。
（２） 36.5％（一部正答32.8％）
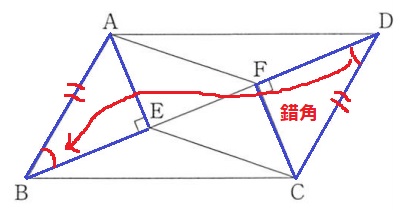
△ＡＢＥと△ＣＤＦにおいて、直角＋平行四辺形の対辺＋（平行→錯角）
＝直角三角形の合同条件の１つ、斜辺と１鋭角が等しい＝合同
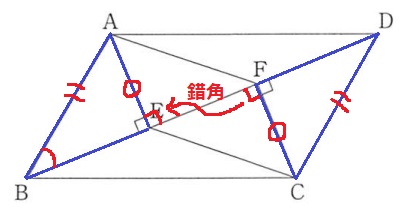
対応する辺が等しいので、ＡＥ＝ＣＦ
また、∠ＡＥＦ＝∠ＣＦＥ＝90°で錯角が等しい→ＡＥ//ＦＣ
１組の対辺が平行で、かつ長さが等しいことから、四角形ＡＥＣＦは平行四辺形となる。
大問３（平面図形２）
（１） 92.7％
1.6×7.2/1.8＝6.4ｍ
（２） 10.0％！
距離や仰角（見上げる角度）を自力で作図する。
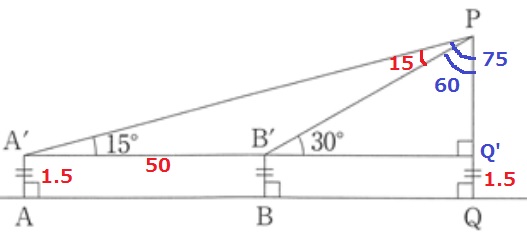
Ａ’やＢ’と同様に、Ｑ’をつくる。
△Ｂ’ＰＱ’の内角は30°－60°－90°の直角三角形（辺の比は１：２：√３）。
△Ａ’ＰＱ’より、∠Ａ’ＰＱ’＝180－（15＋90）＝75°
∠Ａ’ＰＢ’＝75－60＝15°
△Ａ’ＰＢ’は底角がともに15°で二等辺三角形。
Ｂ’Ｐ＝50ｍ
ＰＱ’＝50×１/２＝25ｍ
よって、ＰＱ＝25＋1.5＝26.5ｍ
大問４（関数）
（１） 94.8％
ｙ＝１/２ｘ2に代入して、ＡとＢの座標を出す。
Ａ（－６、18）→Ｂ（４、８）
右に10、下に10なので、傾きａ；－10/10＝－１
Ａから右に６、下に６いくと、切片ｂは18－６＝12
ｙ＝－ｘ＋12
（２）① 10.3％！（部分正答24.6％）
Ｐのｘ座標をｔとおき、必要な座標をｔで表す。
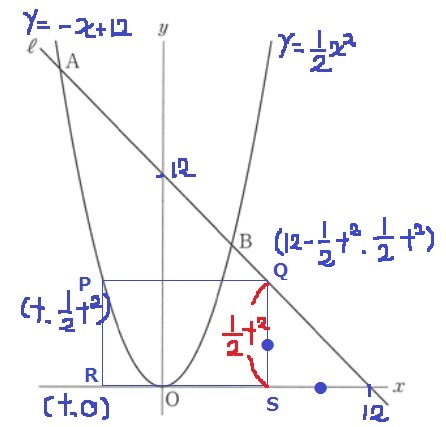
ｙ＝１/２ｘ2より、Ｐ（ｔ、１/２ｔ2）
Ｒ（ｔ、０）
Ｑのｙ座標はＰと同じで１/２ｔ2
ｘ座標は、ｙ＝－ｘ＋12に放り込む。
ｙ＝12－１/２ｔ2
（もしくは、ℓの傾きが－１であることから、うえの●が等しいので、
ＯＳ＝12－●＝12－１/２ｔ2と考えてもいい）
Ｑ（12－１/２ｔ2、１/２ｔ2）
正方形の１辺は等しい。
ＰＱ＝ＰＲより、
12－１/２ｔ2－ｔ＝１/２ｔ2
ｔ2＋ｔ－12
＝（ｔ＋４）（ｔ－３）＝０
ｔ＝－４、３（－６≦ｔ≦４ゆえ条件適合）
各々をｙ＝１/２ｘ2に放り込む。
ｔ＝－４のとき、（－４、８）
ｔ＝３のとき、（３、９/２）
② 1.8％!!（一部正答7.0％）
△ＢＰＱと△ＯＰＱの面積比が１：３になるときのＱ座標を求める。
ＰＱが共通辺なので、これを底辺としたときの高さが１：３になればいい。
Ｑのｙ座標…８×③/④＝６
ｙ＝－ｘ＋12に代入。
Ｑ（６、６）
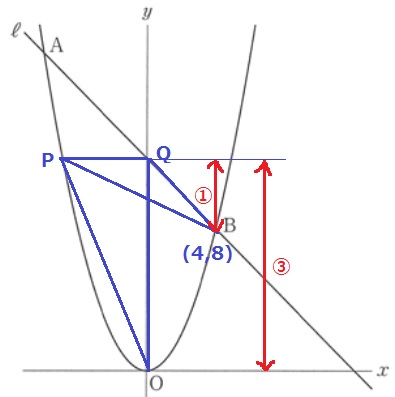
ＰＱはｘ軸に平行な線分。
これをＢよりも上に平行移動させる。
②＝８
Ｑのｙ座標…８×③/②＝12
直線ℓの切片にあたる。Ｑ（０、12）
（６、６）と（０、12）
大問５（空間図形）
（１） 77.5％
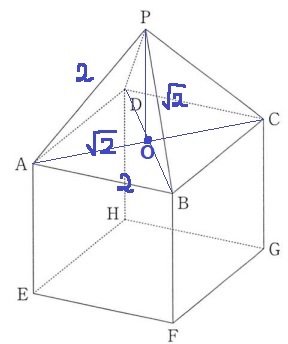
下は１辺２ｃｍの立方体…２×２×２＝８ｃｍ3
上は１辺２ｃｍの正四角錘。
△ＡＯＢも△ＡＯＰも直角二等辺三角形なので、
高さは１：１：√２より、２×１/√２＝√２ｃｍ。
２×２×√２÷３＝４√２/３ｃｍ3
よって、４√２/３＋８ｃｍ3
（２） 23.1％！
ネジレの位置…平行でもない、かつ交わらない。
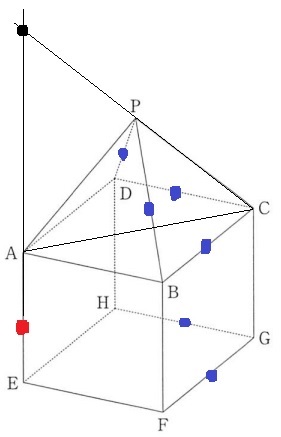
７本じゃないよ！
ＰＣは延長するとＡＥと交わる。
６本
（３） 0.6％!!!（一部正答0.9％）
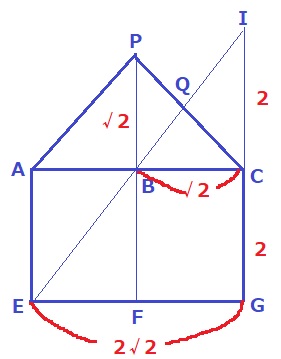
面ＡＥＧＣを正面にして断面図を作成。
ＢとＦはそれぞれＡＣ、ＥＧの中点にくる。
ＥＢとＧＣを延長し、交点をＩとする。
△ＩＢＣ∽△ＩＥＧより、ＩＣ：ＩＧ＝ＢＣ：ＥＧ＝１：２→ＩＣ＝２ｃｍ
△ＰＢＱ∽△ＣＩＱより、ＰＱ：ＱＣ＝ＰＢ：ＩＣ＝√２：２
大問１
（２）中学数学の範囲で計算できるが、高校数学にやや片足つっこんでいる。
対称式は和と積がポイント。
（５）起こりえるパターンが30通りもあるが、正答率は64.1％もあった。
（８）やや細かい判定事項を含むが、６割が正解。
（12）反比例の特徴。あちらの正答率は62.9％だったが、こちらでは77.5％だった。
（16）標本調査。56.2％（一部正答29.2％）の設問が、学校選択では69.5％（一部正答28.0％）。
大問２
（２）三角形の合同から平行四辺形の証明につなげる。
完全正答は３割ちょい。一部正答を含めると７割弱。
大問３
（２）学校選択では図が与えられなかった。作図力が試される。
大問４
（２）②0.6％!!!（一部正答4.9％）→1.8％!!（一部正答7.0％）
ＰＱは動くがＢは固定。
ここからＰＱがＢの上にくる場合と下にくる場合に分ける。
大問５
（２）ＰＣを書いてしまったか。
（３）どこで平面を捉えるか。
断面が直線に見える平面上で相似図形を探してみよう。
＠2020年度 埼玉解説＠
数学…平均67.9点 社会…平均54.6点 理科…平均50.3点 英語…平均51.2点
その他は下記のリンクの目次からどうぞです。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント