2022年度　宮崎県公立高校入試問題過去問【数学】解説

平均48.5点（前年比；－2.0点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－70.9％

（１）　97.7％
－４－（－８）
＝－４＋８
＝４

（２）　91.8％
３/８÷（－１/６）
＝３/８×（－６）
＝－９/４

（３）　91.8％
３（ａ－２ｂ）＋４（－ａ＋３ｂ）
＝３ａ－６ｂ－４ａ＋12ｂ
＝－ａ＋６ｂ

（４）　69.5％
（√３＋√２）²
＝３＋２＋２√６
＝５＋２√６

（５）　75.0％
ｘ²－５ｘ＝６
ｘ²－５ｘ－６
＝（ｘ＋１）（ｘ－６）＝０
ｘ＝－１、６

（６）　71.1％
多角形の外角の和は360°
正十角形の１つの外角は、360÷10＝36°
内角は、180－36＝144°

＠別解＠
ｎ角形の内角の和は180（ｎ－２）
180×（10－２）÷10＝144°

（７）　59.1％
ア：Ａの30回以上は、４＋１＋１＝６人〇
イ：20人の中央値（メジアン）は10番目と11番目の平均。
ＡもＢも25回以上30回未満の階級に含まれる。〇
ウ：範囲（レンジ）＝最大値－最小値
具体的な値はわからないが、Ａの最大は44、最小は５、Ｂの最大は39、最小は０
…で計算しても範囲は40回にならない。×
エ：最頻値（モード）は最もあらわれている値。Ａ…27.5、Ｂ…32.5〇
ウ

（８）　11.4％！

①２辺ＡＢ、ＡＣから等距離→∠ＢＡＣの二等分線
②点Ｃから最も距離が近い→Ｃを通る垂線
これらの交点がＰである。

大問２（確率・方程式）－37.1％

【１】（１）ア…75.5％、イ…55.6％
操作②の後に黒が１枚だけになるには、操作①で何を出すべきか。
イでは理由を記述する。

操作①で５を出して、最初に黒色であったカードＡを白色にすれば、
操作②で何を出しても黒色のカードは１枚だけになる。
よって、答えは５。

（２）　14.7％！
全体は、６×６＝36通り
隣り合う３枚の組み合わせは何か？
黒３枚が必要なので、Ａを含ませなくてはならない。
（Ａ、Ｂ、Ｃ）（Ａ、Ｅ、Ｄ）（Ｅ、Ａ、Ｂ）のいずれかである。

●（Ａ、Ｂ、Ｃ）

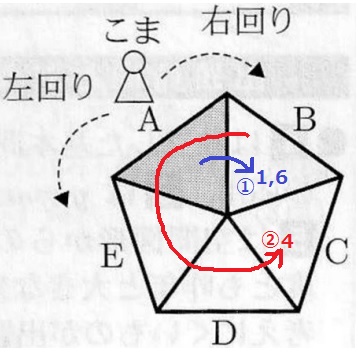
Ｂ→Ｃの順で黒にする。
Ａ→Ｂは進行方向にある隣マスで１か６を出せばいい。
Ｂ→Ｃは進行方向と逆にある隣マスで４を出す。２通り

Ｃ→Ｂの場合。
Ａ→Ｃは１通りしかないが、Ｃ→Ｂは進行方向にある隣マスなので２通り。
計４通り

●（Ａ、Ｅ、Ｄ）
Ａ→Ｅは進行方向の反対隣マスで１通り、Ｅ→Ｄは進行方向隣マスだから２通り。
Ａ→Ｄは１通りで、Ｄ→Ｅは進行方向の反対隣マスで１通り。
計３通り

●（Ｅ、Ａ、Ｂ）
Ａ→Ｅは進行方向反対隣で１通り、Ｅ→Ｂは１通り。
Ａ→Ｂは進行方向隣で２通り、Ｂ→Ｅは１通り。
計３通り
したがって、隣り合う３マスが黒の組み合わせは４＋３＋３＝10通り
確率は、10/36＝５/18

【２】（１）　53.0％
男子ｘ人の75％→0.75ｘ
女子ｙ人の66％→0.66ｙ
「ある」と回答した人数は、0.75ｘ＋0.66ｙ

（２）　11.2％！
答案では求める過程も記述する。
１つは「ある」の人数で等式。
（３年生全員：ｘ＋ｙ人）の70％→0.7（ｘ＋ｙ）
これが前問の人数と符合する。
0.7（ｘ＋ｙ）＝0.75ｘ＋0.66ｙ　…①

もう１つは、新情報の『「ある」の回答者は女子が男子より３人多い』
0.75ｘ＋３＝0.66ｙ　…②

これらの連立を解けばいいが…いかんせん数字が汚い(;`ω´)
①を展開すると、0.7ｘ＋0.7ｙ＝0.75ｘ＋0.66ｙ
0.05ｘ＝0.04ｙ
５ｘ＝４ｙ　…③（ｘ：ｙ＝４：５）

②を100倍して、75ｘ＋300＝66ｙ
これを÷３すると、25ｘ＋100＝22ｙ
③を４倍した25ｘ＝20ｙを代入して、20ｙ＋100＝22ｙ
ｙ＝50
③に代入、ｘ＝50×４/５＝40
全員の人数は、ｘ＋ｙ＝40＋50＝90人

大問３（関数）－55.6％

【１】（１）　41.3％
放物線
*双曲線は反比例。

（２）　89.2％
〇
*ａ＞０は下に凸のグラフ。最小値は原点Ｏだからｘ＝０のとき。

（３）　67.3％
小さくなる
*ａの値を大きくするとグラフの開きは小さくなる。
ｙ＝10000ｘだと、ｘ＝１のときｙ＝10000

【２】（１）　64.1％
ｙ＝１/３ｘ²におのおののｘ座標を代入。
Ａ（－３、３）⇒Ｂ（６、12）
右に９、上に９移動するので、傾きは１。
Ａから右に３、上に３移動して、切片は３＋３＝６
ｙ＝ｘ＋６

（２）　16.0％！
ｙ＝ａｘ²にあるＣ座標を求める。

△ＡＯＣ：△ＣＯＢ＝ＡＣ：ＣＢ＝⑦：②
ＡＢ間のｘ座標の差がありがたいことに９なので、
ＡＢを⑦：②に内分するＣのｘ座標は４（①＝１）
ｙ＝ａｘ²にｘ＝４を代入して、Ｃのｙ座標は16ａ

ＡとＢのｙ座標の差も９。
①＝１→Ｃのｙ座標は10。
16ａ＝10
ａ＝５/８

大問４（平面図形）－28.0％

【１】　70.9％

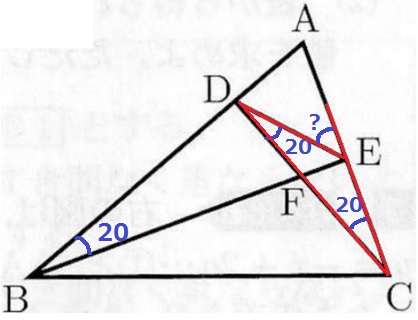
仮定より、∠ＤＢＥ＝∠ＥＣＤ＝20°
ＣＥ＝ＤＥ→△ＣＤＥは二等辺だから、∠ＥＤＣ＝20°
△ＣＤＥに外角定理を適用し、∠ＡＥＤ＝20＋20＝40°

【２】　37.3％
△ＢＤＥ∽△ＤＦＥの証明。

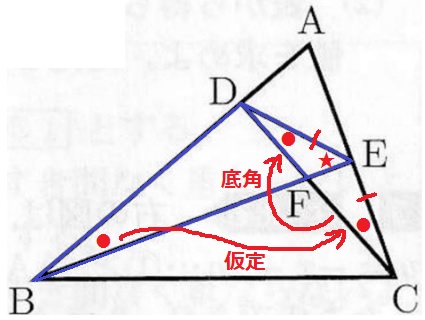
仮定＋二等辺ＣＤＥの底角（●）
共通角（★）
２角が等しく∽。

【３】（１）　3.4％!!

求まりそうで求まらない…。
前問の相似を活用しようとしても、Ｆの位置が定まらないとＤＦとＦＥが出せない。

ＡＢ//ＥＭから、ＢＭ：ＭＣ＝ＡＥ：ＥＣ＝１：１
ＥはＡＣの中点である。
ＡＥ＝ＤＥ＝ＣＥを手がかりに、これらを半径とする円を作図する。
ＡＣは直線だから円の直径。
半円の弧に対する円周角は直角なので、∠ＡＤＣ＝90°

ＢとＣがＤＥについて同じ側にあり、∠ＤＢＥ＝∠ＤＣＥが成り立つので、
円周角定理の逆により、Ｂ・Ｄ・Ｅ・Ｃは同一円周上にある。
∠ＢＤＣ＝90°から直径はＢＣ。半径からＭＥ＝２ｃｍ

△ＡＢＣ∽△ＥＭＣで、ＡＢ＝２×２＝４ｃｍ
ＡＤ＝４－３＝１ｃｍ

二等辺ＥＡＤの底角を×とすると、同位角から∠ＥＡＤ＝∠ＣＥＭなので二等辺ＭＣＥの底角も×。
△ＥＡＤ∽△ＭＣＥの辺の比で、ＥＡ：ＡＤ＝ＭＣ：ＣＥ
ＣＥ＝ｘｃｍとおくと、ｘ：１＝２：ｘ
外項と内項の積で、ｘ²＝２
ｘ＞０、ｘ＝√２
ＣＥ＝√２ｃｍ

（２）　0.2％!!!

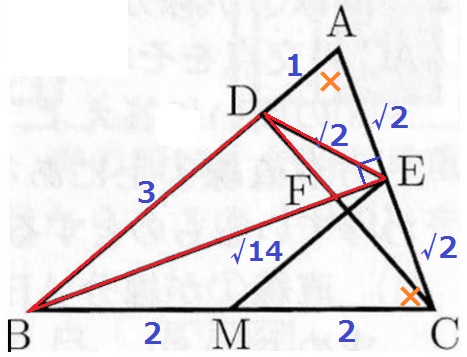
△ＡＢＣは二等辺三角形で、ＢＥは底辺ＡＣの中点Ｅを通過する。
ということは、ＢＥ⊥ＡＣ
△ＡＢＥで三平方→ＢＥ＝√14ｃｍ

△ＤＦＥの面積を求めるので【２】の相似を活用する。
面積比は相似比の２乗だから、
△ＢＤＥ：△ＤＦＥ＝ＢＥ²：ＤＥ²＝（√14）²：（√２）²＝７：１
方針【△ＡＢＥ⇒△ＢＤＥ⇒△ＤＦＥ】
△ＤＦＥの面積は、√14×√２÷２×３/４×１/７＝３√７/28ｃｍ²

大問５（図形応用）－22.4％

【１】　46.4％

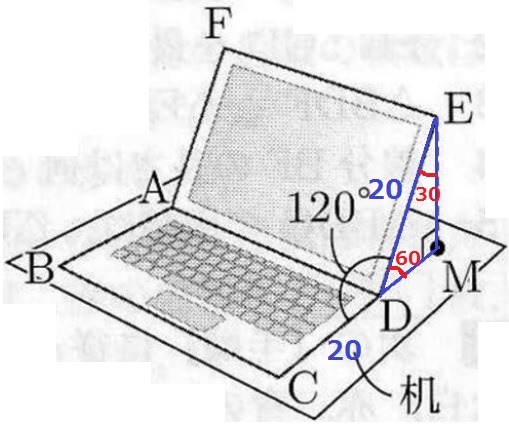
ＥＤ＝ＣＤ＝20ｃｍ
△ＥＤＭの辺の比は１：２：√３なので、
ＥＭ＝20×√３/２＝10√３ｃｍ

【２】（１）　37.0％
扇形ＡＢＦは半径20ｃｍ、中心角120°
20×20×π×１/３＝400/３πｃｍ²

（２）　6.2％!!
長さを調べていく。

底面積は半径18ｃｍ、中心角120°の扇形から半径２ｃｍの扇形を引いたもの。
高さは、30－４＝26ｃｍ
（18×18×π×１/３－２×２×π×１/３）×26
＝（18²－２²）π×１/３×26
＝（18＋２）（18－２）π×26/３
＝20×16×π×26/３
＝8320/３πｃｍ³

【３】　0.0％!!!
むつかしい(;´Д｀)ﾋｨ-

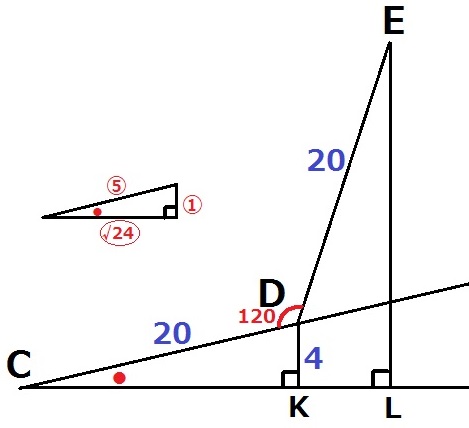
横から見た図を正確に描く。
ＣＤ＝ＥＤ＝20ｃｍ
ＤとＥから垂線をおろし、机との交点をそれぞれＫ・Ｌとする。
求めるべき長さはＥＬである。

この図で使えそうな情報は△ＤＣＫの辺の比。
20：４＝⑤：①
ＣＤ＝⑤、ＤＫ＝①とすると、三平方の定理でＣＫ＝〇√24
内角の１つが∠ＤＣＫ（●）と同じ直角三角形であれば、辺の比は１：５：√24である。

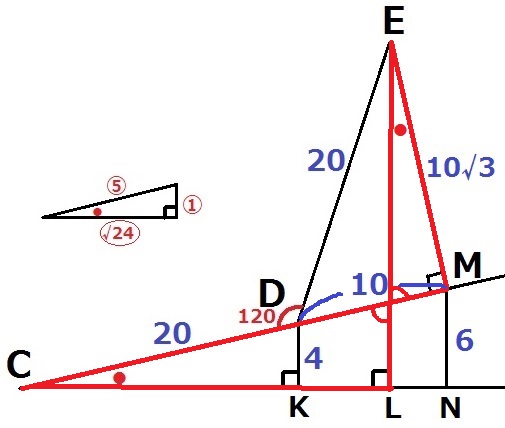
情報が足りないので、【１】で求めたМを追加する。
ＤＭ＝10ｃｍ、ＥＭ＝10√３ｃｍ
Ｍを通る垂線の足をＮとする。
△ＤＣＫ∽△ＭＣＮより、ＭＮ＝４×30/20＝６ｃｍ

ここで赤線の三角形に注目する。
対頂角と90°から、残りの内角（∠ＭＥＬ）は●である。

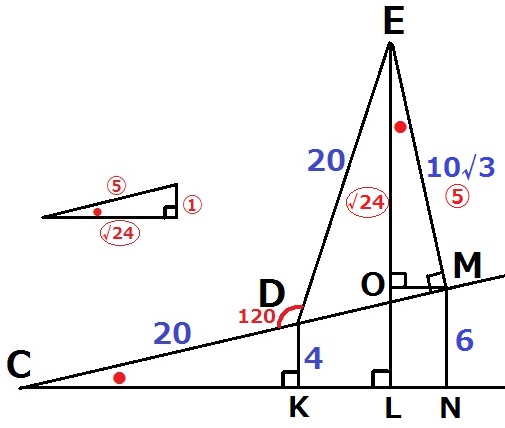
ＭからＥＬに垂線、足をＯとする。
直角三角形ＥＯＭの内角の１つが●だから、辺の比は１：５：√24である。
ＥＯ＝10√３×〇√24/⑤＝12√２ｃｍ
ＯＬ＝ＭＮ＝６ｃｍ
ＥＬ＝ＯＬ＋ＥＯ＝６＋12√２ｃｍ