2024年度　京都府公立高校入試問題過去問・中期【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
６－２×（－５²）
＝６－２×（－25）
＝６＋50
＝56

（２）
２/３（６ｘ＋３ｙ）－１/４（８ｘ－２ｙ）
＝４ｘ＋２ｙ－２ｘ＋１/２ｙ
＝２ｘ＋５/２ｙ

（３）
√32－16/√２＋√18
＝４√２－８√２＋３√２
＝－√２

（４）
（ｘ－ｙ）²－10（ｘ－ｙ）＋25　←ｘ－ｙをＸと置き換える
＝Ｘ²－10Ｘ＋25
＝（Ｘ－５）²　←戻す
＝（ｘ－ｙ－５）²
＝｛７－（－６）－５｝²
＝８²
＝64

（５）
はじめに両辺をｘで割らないこと！
０で割れないので、ｘ≠０という条件がなければｘで割れない。

８ｘ²＝22ｘ
８ｘ²－22ｘ
＝２ｘ（４ｘ－11）＝０
ｘ＝０、４ｘ－11＝０→ｘ＝11/４
ｘ＝０、11/４

（６）
ｙ＝ａｘ²に（ｘ、ｙ）＝（３、－54）を代入。
－54＝９ａ
ａ＝－６
ｙ＝－６ｘ²

（７）

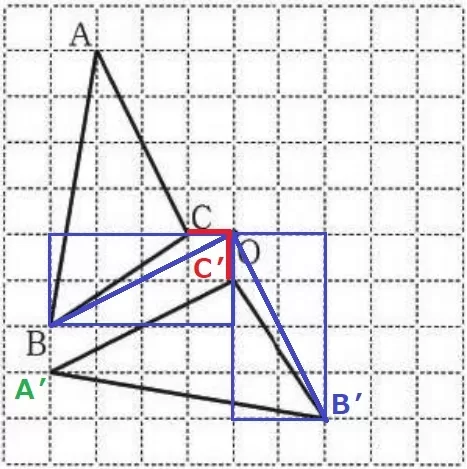
時計回りに270°回転＝反時計回りに90°回転
Ｃが最もわかりやすい。
ＯＢを対角線とする青の長方形の回転移動で捉えてＢ’を定める。
同様にＡも定める。（長方形の対角線はＣＡなどでもいい）

（８）
取り出した１個を戻さずにもう１個取る→同時に２個取るのと同じ。
２個の取り方は、₅Ｃ₂＝10通り
同色の方が少ないので、余事象から求める。
同色は赤２個か白２個の２通りしかない。
異色の確率は、１－２/10＝４/５

大問２（データの活用）

（１）
30分～90分までの度数を合計する。
８＋８＋９＋８＋９＋10＝52人
＠＠

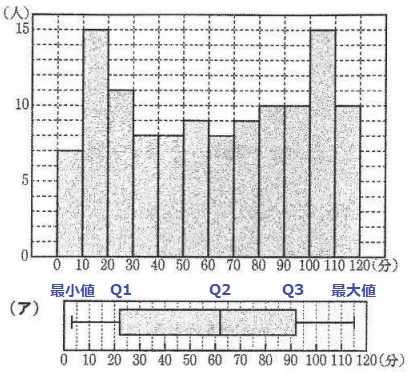
最大値は110～120分の階級→ア・エに絞られる。
２つの違いはQ3（第３四分位数）。
120人のQ3は上位60人の真ん中、上から30番目と31番目の平均。
これが90～100分の階級に含まれるからア。

（２）

ア：Ａ組の中央値は約68分。30人の中央値は15番目と16番目の平均。
たとえば、50分台と70分台の平均でも68分は作れてしまう。×
イ：30人のQ3は上位15人の真ん中、上から８番目。
Ｂ組のQ3から８番目が80分以上なので、80分以上は８人以上いる。〇
ウ：Ｃ組の最大値が複数人いれば、115分は２人以上いる。×
エ：30人のＱ1は下位15人の真ん中である下から８番目。ＤだけQ1が40分を超えている。
Ｄの40分未満は全体の４分の１未満（多くても７人）で最も少ない。×
オ：四分位範囲＝Q3－Q1（箱の長さ）、範囲＝最大値－最小値
四分位範囲が最も大きいのはＡ組で、最も範囲が小さい。〇
イ・オ

大問３（数量変化）

（１）
Ａは自転車を、21－６＝15分間こいだ。
分速600ｍだから、ＰＱ間は600×15＝9000ｍ
＠＠
地点Ｑはスタートから、300＋9000＝9300ｍ
地点Ｑ（21、9300）→ゴール（46、14300）
右に46－21＝25、上に14300－9300＝5000だから、傾きは5000/25＝200
地点Ｑから左に21、下に21×200＝4200移動して、切片は9300－4200＝5100
ｙ＝200ｘ＋5100

（２）

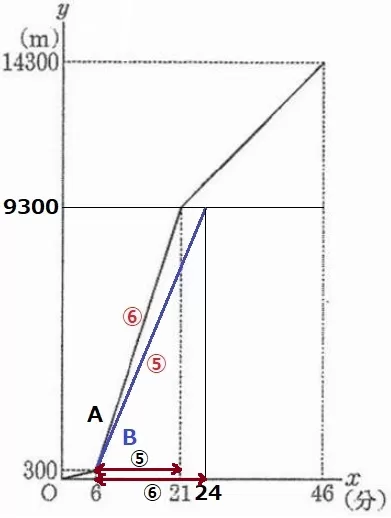
自転車の速さはＡ：Ｂ＝⑥：⑤
時間は逆比で⑤：⑥。
15分＝⑤だからＢの自転車は、15×⑥/⑤＝18分
Ｂが地点Ｑに着くのは、６＋18＝24分後

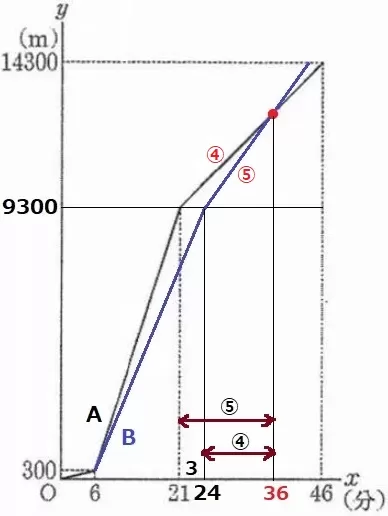
長距離走の速さの比は、Ａ：Ｂ＝④：⑤
時間は逆比でＡ：Ｂ＝⑤：④
差の３分が①にあたるから、Ｂが走ってから３×④＝12分で追いつく。
→スタートから24＋12＝36分後でＡに追いつく。

Ａの速さは前問の傾きから分速200ｍ。
Ｂに追いつかれた場所からゴールまでの距離は、分速200ｍ×10分＝2000ｍ
したがって、14300－2000＝12300ｍ

大問４（空間図形）

（１）

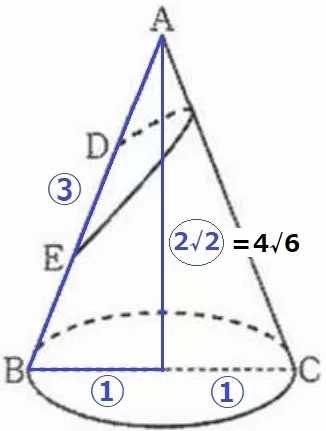
ＡＢ＝③、底面の半径＝①
青線の三角形で辺の比を三平方すると、高さは〇２√２＝４√６ｃｍ
底面の半径は、４√６×①/〇２√２＝２√３ｃｍ
＠＠
ＡＥ＝ＡＢ×２/３＝（２√３×③）×２/３＝４√３ｃｍ
半径…２√３ｃｍ、ＡＥ＝４√３ｃｍ

（２）

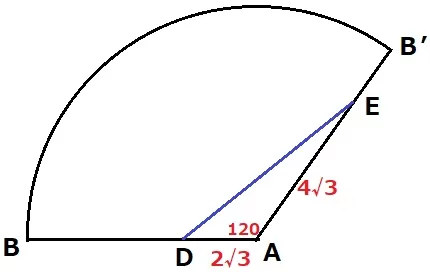
最短距離なので展開図を作成。
扇形の中心角は、360×半径/母線＝360×①/③＝120°

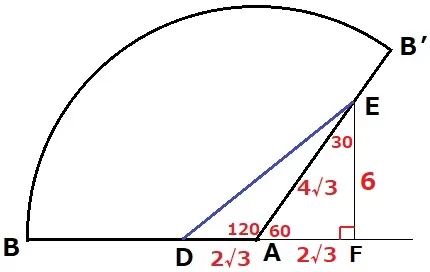
Ｅから垂線をひき、ＤＡの延長との交点をＦとする。
∠ＥＡＦ＝180－120＝60°→△ＡＥＦは内角が30°－60°－90°
→辺の比は１：２：√３だから、ＡＦ＝２√３ｃｍ、ＥＦ＝６ｃｍ
△ＤＥＦで三平方→ＤＥ＝２√21ｃｍ

大問５（平面図形）

（１）

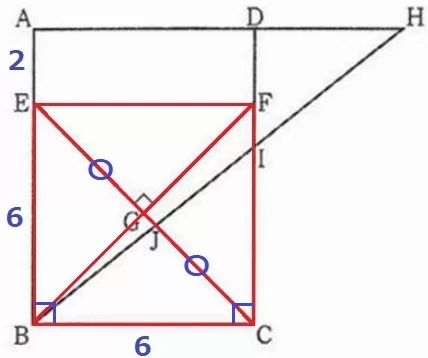
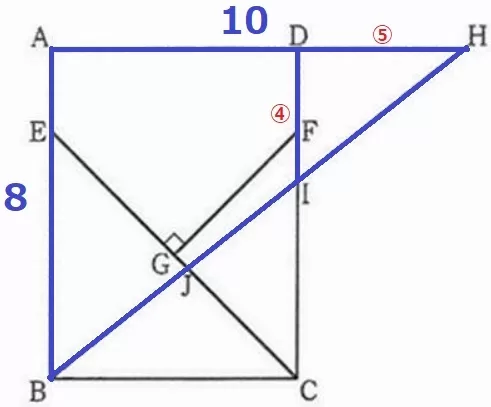
ＥＢ＝８－２＝６ｃｍ
ＢＧとＥＦに補助線。
△ＥＢＣは直角二等辺で、Ｇは底辺ＥＣの中点→ＢＧ⊥ＥＣ、Ｂ・Ｇ・Ｆは一直線に並ぶ。
ＢＦを対称の軸として左右対称、∠ＢＥＦ＝∠ＢＣＦ＝90°
四角形ＥＢＣＦは１辺６ｃｍの正方形で、対角線ＢＦとＣＥの交点がＧである。
△ＣＦＧ＝正方形ＥＢＣＦ÷４＝６×６÷４＝９ｃｍ²

（２）

△ＡＢＨ∽△ＤＩＨより、ＤＩ：ＤＨ＝④：⑤

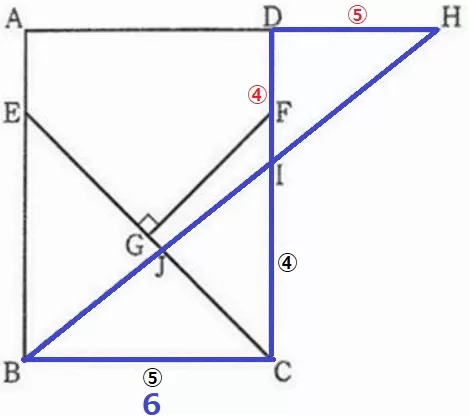
△ＤＩＨ∽△ＣＩＢより、ＣＩ：ＣＢ＝④：⑤
ＣＩ＝６×④/⑤＝24/５ｃｍ

（３）

（１）で△ＣＦＧを求めたので、これから△ＣＩＪを引けばいい。
△ＥＢＪ∽△ＣＩＪより、ＢＪ：ＪＩ＝６：24/５＝⑤：④
△ＣＩＪの面積は、△ＢＣＩ×④/⑨＝６×24/５÷２×④/⑨＝32/５ｃｍ²
四角形ＦＧＪＩの面積は、９－32/５＝13/５ｃｍ²

大問６（規則）

（１）

ｎ＝５のとき、弦の本数は＋４して10本。

（２）

規則を見つける。
【１、３、６、10…】は１から連続する整数和（三角数）で、末項（最後の数）がｎ－１である。

ｎ＝41のとき、末項は41－１＝40
→１＋２＋３＋…40を計算すればいい。
（１＋40）×40÷２＝820本

（３）
１～（ｎ－１）までの和が1953になる。
（１＋ｎ－１）（ｎ－１）÷２＝1953
ｎ（ｎ－１）＝3906

連続する２数の積が3906になる。
60×60＝3600だから、ｎは60より少し上。
位の和が９の倍数→3906は９の倍数だから63を含む。
62×63か63×64。一の位６から62×63＝3906
ｎ＝63