2020年度　三重県公立高校入試過去問・前期【数学】解説

問題はコチラ→ＰＤＦファイル
2020年度・三重後期（数学）解説はコチラ。

大問１（小問集合）

（１）
（－３）²＋２×（－５）
＝９－10＝－１

（２）
（４ｘ－３）/２－（６ｘ－７）/５
＝｛５（４ｘ－３）－２（６ｘ－７）｝/10
＝（20ｘ－15－12ｘ＋14）/10
＝（８ｘ－１）/10

（３）
（－４ｘｙ）²×（－３ｘ）
＝16ｘ²ｙ²×（－３ｘ）
＝－48ｘ³ｙ²

（４）
４ｘ－３ｙ＝－７　…①
５ｘ＋９ｙ＝－13　…②
加減法がいいかな？①×３＋②
12ｘ－９ｙ＝－21
＋)５ｘ＋９ｙ＝－13
17ｘ　　　　＝－34
ｘ＝－２
①に代入。－８－３ｙ＝－７
ｙ＝－１/３
ｘ＝－２、ｙ＝－１/３

（５）
５√６＋２√24－６√３/√２
＝５√６＋４√６－３√６
＝６√６

（６）
（ｘ＋４）（ｘ－６）＝６ｘ－39
ｘ²－２ｘ－24＝６ｘ－39
ｘ²－８ｘ＋15
＝（ｘ－３）（ｘ－５）＝０
ｘ＝３、５

（７）
ｘ＝－５のとき、ｙ＝25ａ
ｘ＝－３のとき、ｙ＝９ａ
（９ａ－25ａ）/｛－３－（－５）｝
＝－16ａ/２＝－８ａ＝２
ａ＝－１/４

*ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（－５－３）＝２
－８ａ＝２
ａ＝－１/４

（８）
５×５×π×６÷３＝50πｃｍ³

（９）
△ＡＢＣで外角定理。
40＋〇〇＝●●　←÷２
20＋〇＝●
△ＥＢＣの外角定理から、∠ＢＥＣ＝20°

（10）
難しい:;(∩´＿`∩);:

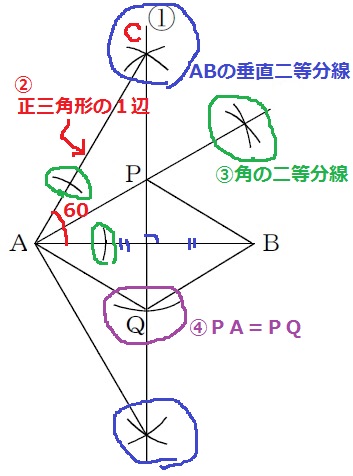
①まず、菱形の対角線は各々を垂直に二等分するので、ＡＢの垂直二等分線を作図。
この線上のどこかにＰとＱがある。
ＡからＰの位置を特定したい。
∠ＡＰＢ＝120°ということは∠ＰＡＱ＝60°
∠ＰＡＢ＝30°、30°は60°の半分。
②ＡＢを１辺とする正三角形ＡＢＣをつくる。
垂直二等分線との交点がＣ→∠ＣＡＢ＝60°
③∠ＣＡＢを二等分。この線と①の垂直二等分線の交点がＰとなる。
④Ｐを中心にＰＡの長さをとり、①との交点がＱとなる。
（△ＡＰＱも正三角形なので、ＡＰ＝ＡＱでもよい）

大問２（標本調査・確率）

（１）①
ア・イの度数が不明だが、
29－（２＋３＋８＋５＋４）＝７だから、ア＋イ＝７
最頻値は６以上～８未満の階級となる。
解答するときは階級値で答えること！７点

②
29の中央値は、（29＋１）÷２＝15番目の値
15番目の値が６以上８未満にならないようにする。

ア＋イ＝７なので、仮に７人すべてがアとすると、
15番目の値は６以上８未満の階級にはいってしまう。
よって、15番目の値は８以上の階級に含ませる。
２以上８未満の度数の合計は13だから、アが２以上だと15番目が６以上８未満となりＮＧ。
よって、ア＝０、１

（２）①
ｘとｙが同じ数。
１回目に”何か”を出す。
２回目にその”何か”が出る確率は１/６

②
（ｘ、ｙ）＝（２、４）（４、２）
この２通りしかない。
全体は６×６＝36通りなので、２/36＝１/18

③
１/９＝４/36
すなわち、起こりえる場合の数は４通り。
反比例の比例定数ａはｘとｙの積。
ｘｙの組み合わせが４通りとなるａを探す。

４通りということはペアが２組なので、ａは偶数である。
ａ＝２、４、６…と総当たりで調べていくと、
ａ＝６のとき
（ｘ、ｙ）＝（１、６）（６、１）（２、３）（３、２）
ａ＝12のとき
（ｘ、ｙ）＝（２、６）（６、２）（３、４）（４、３）
これしかない。
したがって、ａ＝６、12

大問３（数量変化）

（１）
ｙ＝40までは、水面の変化の割合が等しい。
ｘ＝１のとき、ｙ＝４だから、ｙ＝４ｘ（０≦ｙ≦40）
ｙ＝24のとき、24＝４ｘ
ｘ＝６

（２）
１分後の水量を求める。
50×60×４＝12000ｃｍ³
12分後は、12000×12＝144000ｃｍ³

（３）
水槽全体の容積は、
（80×60－40×30）×60　←正面から見たときの面積×奥行き60ｃｍ
＝216000ｃｍ³
１分あたり水は12000ｃｍ³はいるので、
216000÷12000＝18分後

（４）
水深０～40ｃｍは底面積が小さいのでｙの変化が大きい。
水深40～60ｃｍは底面積が大きくなるので、ｙの変化が小さくなる。
イ

（５）
ｙ＝４ｘ（０≦ｙ≦40）から、
ｙ＝40のとき、ｘ＝10
18分後に満水で水深は60ｃｍとなる。
（10、40）→（18、60）
右に８、上に20なので、傾きａ＝20/８＝５/２
ｙ＝５/２ｘ＋ｂに（10、40）を代入。
40＝５/２×10＋ｂ
ｂ＝15
ｙ＝５/２ｘ＋15

大問４（空間図形・式の変形）

（１）
体積比は辺の比の３乗。

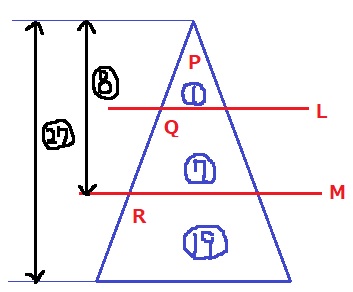
Ｐ＝１×１×１＝①
Ｑ＝２×２×２－①＝⑦
Ｒ＝３×３×３－⑧＝⑲
Ｒの体積は、28×⑲/⑦＝76ｃｍ³

（２）①ウ
２ｘ²＋５ｘ＝０の式をｘで割って、２ｘ＋５＝０に変形できない理由を述べる。
ポイントは右辺の『０÷ｘ＝０』
数学的な細かい話もあるようだが…サボは結果だけ覚えています。
０÷３…ＯＫ
３÷０…ＮＧ
『無を割ることはできるが、無で割ることはできない』
解答は、ｘ＝０のときに０÷ｘができないから変形が正しくないとなる。

なぜ、割る数に０はダメなのか？
代数的にわかりやすい説明は、割られる数を□とおき、
６÷２＝３→□÷２＝３と置き換えると、□＝３×２＝６が成り立つ。
□（０以外の数）÷０＝ｎでは□＝ｎ×０＝０となり、条件に合わない。
解がない（不能）となる。

ちなみに、０÷□＝０とすると、０＝□×０＝０となり、□は何を代入しても成り立つ。
解が定まらない（不定）となる。

大問５（平面図形）

（１）
△ＢＤＥ≡△ＤＧＦの証明。

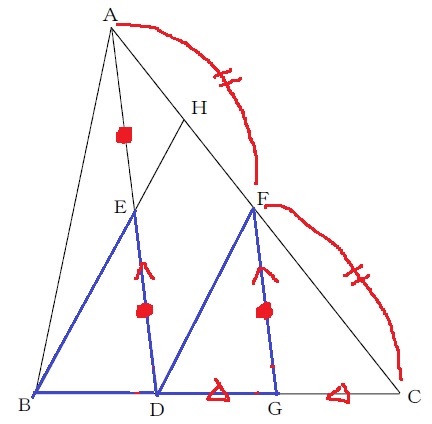
ＡＤ//ＦＧ、ＡＦ＝ＦＣより、平行線と線分の比からＤＧ＝ＧＣ
△ＡＣＤで中点連結定理→ＦＧ＝●とすると、ＡＤ＝●●
ＥはＡＤの中点なので、ＥＤ＝●

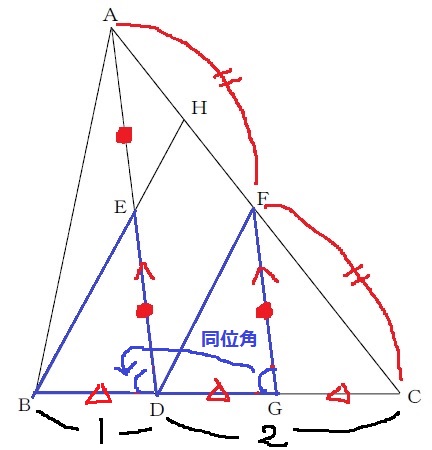
ＤＧ＝ＧＣ＝△とする。
ＢＤ：ＤＣ＝１：２から、ＢＤ＝△
同位角とあわせると、２辺とあいだの角が等しくなり合同。

（２）

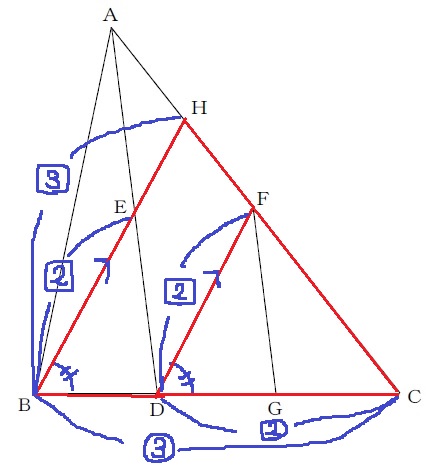
前問の合同より、∠ＥＢＤ＝∠ＦＤＧから同位角が等しく、ＢＨ//ＤＦ
△ＦＣＤ∽△ＨＣＢより、ＦＤ：ＨＢ＝ＤＣ：ＢＣ＝□２：□３
ＢＥ＝ＤＦ＝□２だから、ＥＨ＝□１
よって、ＢＥ：ＥＨ＝２：１

（３）

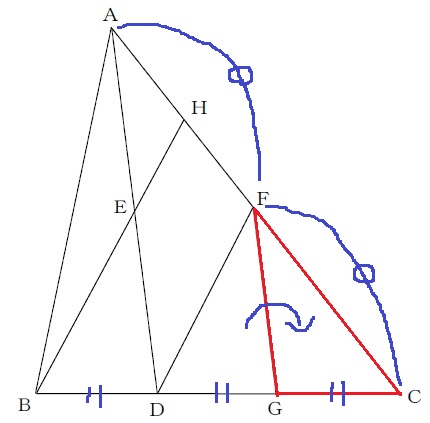
△ＦＧＣは△ＤＧＦと底辺と高さが共通するので、△ＡＢＣ：△ＦＧＣの面積比を考える。
必要な情報だけを取り出すと、うえの図になる。
隣辺比から、△ＡＢＣ：△ＦＧＣ＝２×３：１×１＝６：１
△ＡＢＣ：△ＤＧＦ＝６：１

（４）
奇抜な出し方でやりづらい:;(∩´＿`∩);:
ＦＧ＝ａとしたとき、ＡＩをａであらわす。
ひとまず、文字式の要領で求めたいＡＩの長さをｘとおく。

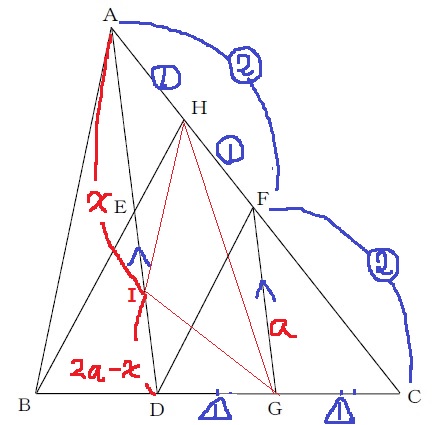
ＦＧ：ＡＤ＝１：２から、ＡＤ＝２ａ
ＩＤ＝２ａ－ｘ

（３）の△ＦＣＤ∽△ＨＣＢから、ＨＦ：ＦＣ＝①：②で、
ＡＦ＝ＦＣ＝②から、ＡＨ＝ＨＦ＝①となる。（ＨはＡＦの中点）

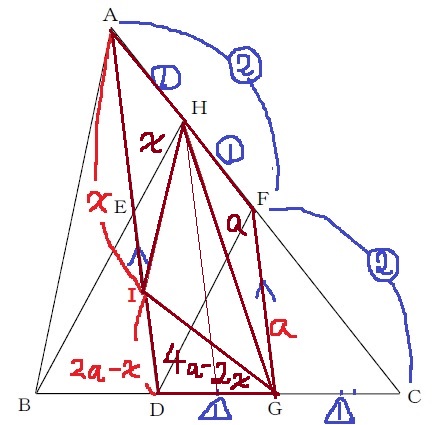
おのおのの面積比を隣辺比から計算。
△ＡＨＩ…ｘ×①＝【ｘ】
△ＧＦＨ…ａ×①＝【ａ】
△ＤＧＩ…底辺は２ａ－ｘだが、問題は高さ。
△ＤＧＩはＡＦと接していないが、
平行線はどこも高さが等しいので、高さの比はＡＦ基準で②と計算してもＯＫ。
（２ａ－ｘ）×②＝【４ａ－２ｘ】

等式を立てる。
ｘ＋ａ＝３（４ａ－２ｘ）
７ｘ＝11ａ
ｘ＝11/７ａ
ＡＩ＝11/７ａ

大問１
（９）中学入試にも出てくる。いくつかあるパターンのうちの基本形なのでおさえておきたい。
（10）作図の正答率は悪いと思われる。120°ではなく60°に着目する。
大問３
標準レベルなので取りこぼしたくない。
大問４
（１）パターン学習で攻略できるが、正答率は高くなさそう。３乗から上の部分を引く。
（２）ほぼ知識問題。
大問５
テクニカルな設問で難易度は高い。
（３）△ＦＧＣに場所を変えて隣辺比。
（４）難問。比の扱いに相当慣れていないと解けない。他の見直しにまわったほうがいい。
公立高校入試解説ページに戻る