2017年度　千葉県公立高校入試【前期】数学解説

平均点５１．４点

問題はコチラから→ＰＤＦファイル

大問１（計算）－86.3％

（１）　98.8％
（－８）×（－２）
＝１６

（２）　87.1％
６－（－２）²÷４/９
＝６－４×９/４
＝６－９
＝－３

（３）　91.8％
２（ｘ－３ｙ）－３（ｘ－４ｙ）
＝２ｘ－６ｙ－３ｘ＋１２ｙ
＝－ｘ＋６ｙ

（４）　64.6％
４ｘ－３ｙ＝１５をｙについて解く。
３ｙ＝４ｘ－１５　　←－３ｙと１５を移項して、左右反転
ｙ＝４/３x－５

（５）　90.4％
３√５－√８０＋√２０
＝３√５－４√５＋２√５
＝√５

（６）　84.8％
３ｘ² ＋７ｘ＋１＝０
解の公式を利用する。
ｘ＝(－７±√３７)/６

大問２（小問集合）－41.7％

（１）　71.1％
選択肢の並びがバラバラだが、三角形に騙されてはならない。
回転体の底面は円となる。エ：円錐

（２）　56.9％
１０人のメジアンは５．５人目、つまり５人目と６人目の平均。
５人目は２３、６人目は２４だから、メジアンは２３．５。

（３）　45.5％
一次方程式。
父が出発してからｘ分後に追いついたとすると、
あきこが進んだ距離・・６０×１４＋６０ｘ
父が進んだ距離・・２００ｘ
これらが等しいので、６０×１４＋６０ｘ＝２００ｘ
ｘ＝６　→６分後
—————
中学受験経験者であれば旅人算でも対処できます。
１４分後にあきこと父は、６０×１４＝８４０ｍ離れている。
同じ方向に進むので、１分あたり２００－６０＝１４０ｍ差が縮まる。
よって、８４０÷１４０＝６分後に追いつく。
「父が出発してから」なので14は足さない。

（４）　33.1％！
問題文の文字数が多いが、ようは３枚ひいて順番に箱に入れ、
カードの番号と順番（箱の数字 ）が１度だけ等しくなる確率を求める。
１回目だけ等しくなる組み合わせを樹形図で調べる。

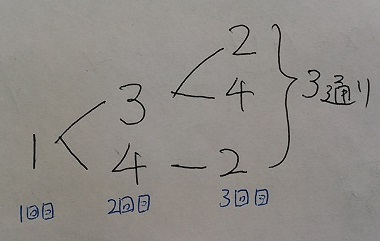
２回目、３回目も同じなので、カードと箱の数字が１度だけ等しくなる組み合わせは、
３×３＝９通り
４枚から３枚ひいて並べる→４×３×２＝２４通り
よって、９/２４＝３/８

（５）　1.9％!!
円の作図問題。
中心点がAB上にあったり、円がℓと接していたり、Bが円周上にくるなど、
どれを使えばよいのかわからず、もどかしい気分にさせられる。
　
完成図を予想して、実際に描いてみよう。
円の内部に拘泥していると真相は見えてこない。
無駄に広い左側のスペースには意味がある・・。
　
ポイントは「Bが円周上にくる」こと。
中心点がＡＢ上にあり、点Ｂが円周上にくるということは、
ＯＢは円の半径で、半径はＡＢ上にある。半径と接線は垂直の関係。

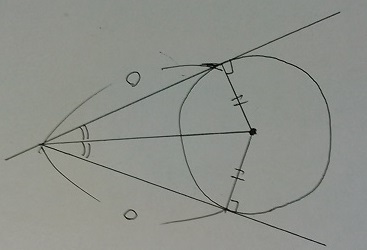
接線をひいてみると、もう１つの接線との間の角の二等分線上に円の中心点がくる。
上と下の直角三角形は合同（斜辺と他の１辺が等しい）。内心円でみたことあるはず。
①接線→②角の二等分線で中心点を求める。

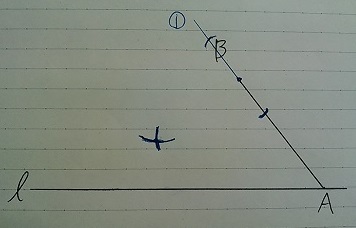
まずはB方向に延長線をひき、Bを通る半直線ABに垂直な線を作成。

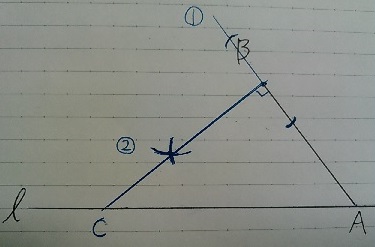
ℓとの交点をCとおく。
∠BCAの二等分線と線分ABとの交点が中心点Oとなる。

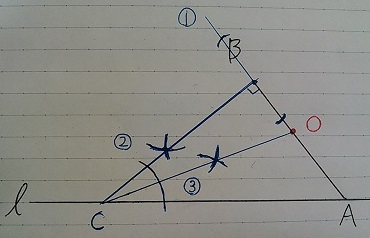
中心点が見つかる。
問題文で指示されているOはきちんと書くこと！

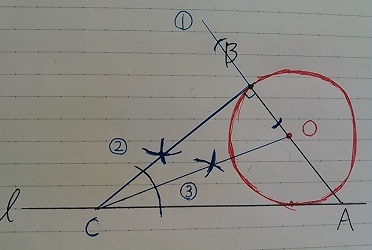
あとは、OからBまでの距離をとってグルっと１周。

大問３（関数）－51.7％

（１）　74.2％
毎度お馴染みの傾き問題。
ｙ＝１/２x＋２のｘに４を代入してＢ座標を求める→Ｂ（４、４）
これをｙ＝ａｘ²へ放り込む。
４＝４² ａ＝１６ａ
ａ＝１/４

（２）　65.8％
典型的な等積変形。

ｘ座標に向かってＡとＢを降下させる。
ｘ座標もわかっているし、切片から高さ２もわかる。
６×２÷２＝６ｃｍ²

（３）　15.1％！
Ｈを作図
ＡＨの長さとＨＢの長さの比は、ｘ座標の距離で考える。
Ｈのｘ座標さえわかれば、正解は目前。

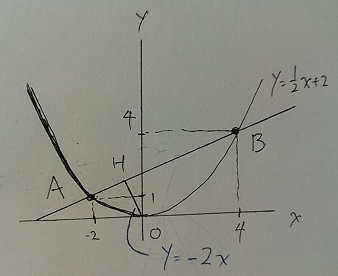
２直線が垂直に交わる　→　傾き×傾き＝－１
傾き１/２と垂直に交わるので、－1÷１/２＝－２
原点を通るから、線分ＯＨは ｙ＝－２ｘ
　
ＯＨとＡＢの交点から方程式
－２ｘ＝１/２x＋２
ｘ＝－４/５　・・Ｈのｘ座標
　
ｘ座標の距離を求める。距離計算なので絶対値。
ＡＨ：２－４/５＝６/５
ＨＢ：４/５＋４＝２４/５
ＡＨ：ＨＢ＝６/５：２４/５＝６：２４＝１：４

大問４（平面図形）－49.5％

（１）問題集で見慣れた形ゆえ、経験を積んでいる人には有利か。
（ａ）誘導に従う。ウ：∠ＡＣＥ　92.3％
（ｂ）オ：２辺とその間の角　　92.5％
（ｃ）６点―12.1％！　３点―6.0％　無答―45.2％
正三角形の証明→３辺が等しいか、３つの角が等しいことを説明する。
辺だとＤＥが変なところにあるので、角から攻める。

∠ＡＢＣは正三角形の内角の１つなので６０°
円周角定理から∠ＡＤＥ＝６０°
（１）の合同図形からＡＤ＝ＡＥなので
（この時点で）△ＡＤＥは二等辺三角形であることがわかる。
底角は等しいので、∠ＡＥＤ＝６０°（図の赤いところは全て６０°）
△ＡＤＥにおいて、残りの角である∠ＤＡＥを計算すると６０°
３つの角が全て６０°となることから、△ＡＤＥは正三角形であるとわかる。

正三角形は特別な二等辺三角形！
一度、二等辺三角形であることを指摘し、
そのうえで正三角形であることを指摘する流れ。

（２）　1.0％!!
できそうでできない、やれそうでやれない(;´Д｀)
しかし、適切な補助線を１本ひいてしまえば優雅に解答できる。
　点Ａを通り、ＤＣに垂直な線をひく。交点はＨ

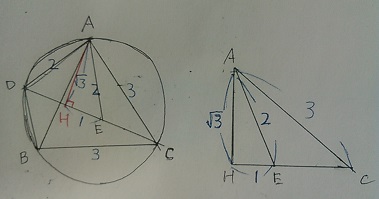
△ＡＨＥは正三角形ＡＤＥの右半分で、１：２：√３とお馴染みの直角三角形。
ＡＨ＝√３がわかれば、△ＡＨＣで三平方を駆使すれば終わり。
ＣＨ＝√（３²－√３^２）＝√６
よって、ＣＥ＝√６－１

大問５（規則）－19.2％

（１）　38.0％
正六角形の周りに、小さな正三角形を反時計回りに敷き詰めていく規則。
１辺３ｃｍの正六角形であれば図４に１周書き足せば数えられるので、努力で乗り切れる。
計算で求める場合は一気に求めようとはせず、６分の１サイズに区切る。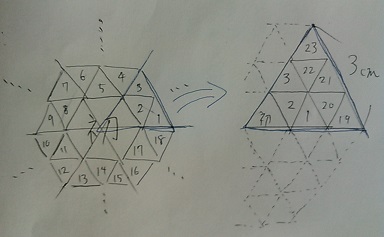
↑初めの正六角形は三角形のタイルではないので、【初】と書いてある。
６０°ずつ６つにカッティング。１切れを数えて６倍すればいい。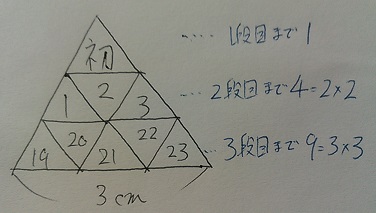
１切れをピックアップ。【初】を上にもってきた。
すると、ｘ段目までの△の枚数は、ｘの平方数であることに気付く。
【初】は正六角形の一部なので三角形のタイル数としてカウントしてはならない。
　
１辺３ｃｍの場合、１切れあたりの三角形の枚数は、３×３－１＝８個
全体で、８×６＝４８個

（２）　26.7％！
上の規則に気付ければ、快速で求められる。
三角形のタイルが１４４枚なので、正六角形の【初】まで含めると、
１４４＋６＝１５０枚分の△がある。
１切れあたり、１５０÷６＝２５個
２５＝５×５だから、大きい正六角形の１辺は５ｃｍとなる。

（３）①　8.0％!!
１辺８ｃｍなので、１切れあたりの三角形のタイルは８×８－１＝６３個
全体で、６３×６＝３７８枚
「赤→緑→緑→青→青→青」で１周するので、
３７８÷６＝６３周する。
１周あたり、緑は２枚だから、
２×６３＝１２６枚

②　4.2％!!
最も使用する色は青なので、青に着目する。
１周あたり青は３枚だから、４００÷３＝１３３周・・余り青１枚分
つまり、三角形のタイルは、６×１３３＋４（赤緑緑青）＝８０２枚
【初】の部分を含め、△の枚数は８０２＋６＝８０８
（６枚中３枚が青なのだから、青の合計が４００枚ならばト－タルで８００枚程度ですね）
　
表にまとめて数えてもよいが、慣れている人は計算で求めてみよう。
最も大きい正六角形の１辺の長さを〇ｃｍとおくと、
〇×〇×６＜８０８（ただし、〇は最も大きい自然数）
〇×〇＜134・・
１１×１１＝１２１、１２×１２＝１４４だから、
〇＝１１
よって、１１ｃｍ。

合同図形は全体ではなく、一部で考える。
三角形のタイルの枚数≠△の枚数（はじめの正六角形はタイル数に含まれない）
△の枚数は平方数で求める。
公立高校入試解説ページに戻る