2022年度　鹿児島県公立高校入試問題過去問【数学】解説

平均39.0点（前年比；－8.3点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－64.6％

（１）①　96.8％
４×８－５
＝32－５
＝27

②　95.0％
１/２＋７/９÷７/３
＝１/２＋１/３
＝５/６

③　79.2％
（√６＋√２）（√６－√２）
＝６－２
＝４
*誤答は２が多かった。

④　47.9％
１～99までの３の倍数は、99÷３＝33個
１～９までは、９÷３＝３個
10～99までは、33－３＝30個
*誤答は33個が多かった。３、６、９を含めていたと思われる。

⑤　35.0％
２つの三角錐の相似比は１：２。
体積比は相似比の３乗だから１：８。
三角錐Ａ—ＢＣＤの体積はＡ—ＥＦＧの８倍。
*誤答は４倍が多かった。

（２）　59.1％
３ａ－２ｂ＋５＝０
２ｂ＝３ａ＋５
ｂ＝（３ａ＋５）/２
*誤答は（３ａ－５）/２や（－３ａ－５）/２が見られた。

（３）　57.4％
全体は３×４＝12通り
√ａｂが自然数になる⇒積ａｂが平方数。
Ａ：【２】【２²】【２・３】
Ｂ：【２・３】【７】【２³】【３²】
素数７は無い。
【２】×【２³】
【２²】×【３²】
【２・３】×【２・３】
計３通りで、確率は３/12＝１/４
*誤答は１/12や１/６が多かった。

（４）　63.3％

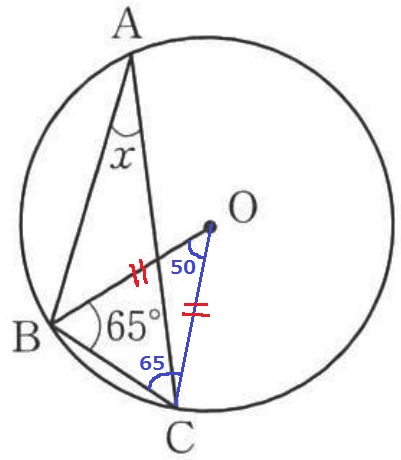
ＯＣに補助線。
半径より△ＯＢＣは二等辺三角形で、∠ＢＯＣ＝180－65×２＝50°
ｘは弧ＢＣに対する円周角だから、ｘ＝50÷２＝25°
*誤答は30°が多かった。

（５）　47.9％
愚直に計算すると時間が足りないので、概算で対処する。

5151：11092≒①：②とする。
①×13％＝0.13
②×50％＝１
0.13を８倍すると１に近い。
ウ
*誤答はア、イが多かった。選手数や女性の選手数の割合で計算したものと考えられる。

大問２（小問集合２）－45.7％

（１）　14.8％！
ａ＜０だから上に凸のグラフ。
ｘ＝－５のとき、最小値ｙ＝25ａ
ｘ＝０のとき、最大値ｙ＝０
25ａ≦ｙ≦０
*誤答として０≦ｙ≦25ａ、－25ａ≦ｙ≦０が見られた。
ａを負の数として捉えられていないものと考えられる。

（２）　62.8％
平行四辺形になるための条件
①２組の対辺が平行②２組の対辺が等しい③２組の対角が等しい
④対角線がおのおのの中点で交わる⑤１組の対辺が平行かつ長さが等しい
イは⑤が成り立つ。

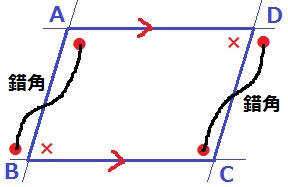
エが曲者。
∠Ａと∠Ｃ（●）を錯角で移動させると、反対側の∠Ｂと∠Ｄ（×）も等しい。
２組の対角が等しいので平行四辺形となる。
イ・エ
*誤答はアが多かった。

＠同側内角＠

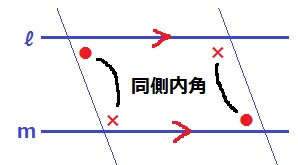
錯角や同位角は有名だが、図の●と×の位置にある角の関係を同側内角というらしい。
ℓ//ｍのとき、同側内角の和は180°になる。

（３）　53.4％

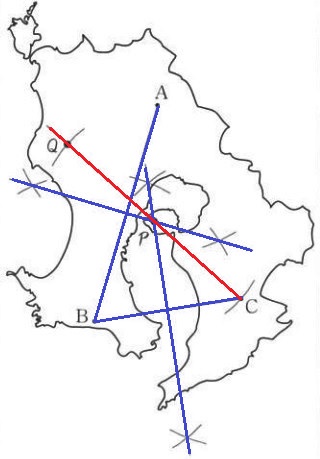
『３点Ａ・Ｂ・Ｃから等距離にあるＰ』
３点を通る円の中心点の作図。
ＡＢ、ＢＣ、ＣＡのうち、２つの垂直二等分線の交点がＰとなる。
すると、桜島にＰがくる。
『ＣをＰを回転の中心として180°回転移動したＱ』
ＣＰを延長。Ｐに針を合わせ、ＰＣの長さを反対側に移す。交点がＱ。
*誤答では角の二等分線をとったものや点Ｃを回転の中心としたものがあった。

（４）①　68.1％
全体の度数は100人で、60分以上の度数の和は40人。
1200×40/100＝480人
*誤答として40人が見られた。12倍しなかったものと考えられる。

②　31.4％！
答案では方程式と計算過程も記述する。
１つ目は度数の和で等式。
ｘ＋ｙ＝100－（８＋27＋13）
ｘ＋ｙ＝52　…①

２つ目は平均値から等式。
総和は階級値を使って求める。
10×８＋30ｘ＋50ｙ＋70×27＋90×13＝54×100
30ｘ＋50ｙ＝2260　←÷10
３ｘ＋５ｙ＝226　…②

①と②で連立を組む。
これを解いて、ｘ＝17、ｙ＝35
*立式はできたが計算ミスもあった。また、仮平均を用いた解答があった。

大問３（関数）－24.8％

（１）　62.3％
底辺ＡＢ＝８－２＝６
高さはｙ座標の差で、12－４＝８
△ＡＢＣの面積は、６×８÷２＝24

（２）①　27.1％！

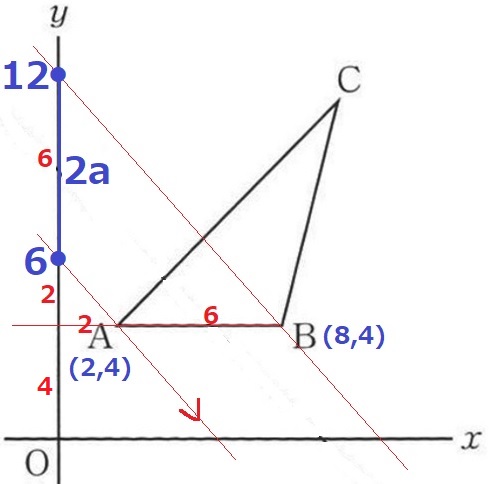
傾きが－１なので右下45°→直角二等辺がでてくる。
Ａを通る直線の切片は、４＋２＝６
Ｂを通る直線の切片は、４＋８＝12
６≦２ａ≦12　←÷２
３≦ａ≦６
*誤答として２≦ａ≦８や点Ｃを代入しているものが見られた。

②　13.1％！

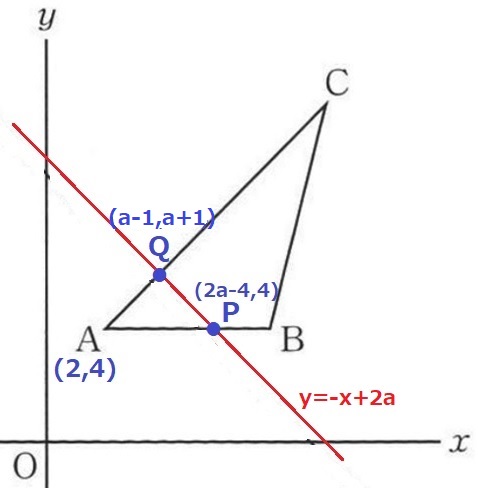
Ｑはｙ＝－ｘ＋２ａとＡＣの交点。
ＡＣの式を求める。
Ａ（２、４）⇒Ｃ（10、12）
右に８、上に８で傾きは１。
Ａから左に２、下に２移動して、切片は４－２＝２
ＡＣ；ｙ＝ｘ＋２

Ｑの座標を求める。
ｘ＋２＝－ｘ＋２ａ
ｘ＝ａ－１
ｙ＝ｘ＋２＝（ａ－１）＋２＝ａ＋１
Ｑ（ａ－１、ａ＋１）
*誤答としてａを用いて表せていないものが多かった。
また、直線ＡＣの方程式を求められていないものもあった。

③　3.8％!!
答案では求める過程も記述する( ;∀;)
これまでの解答を利用する。

Ｐのｙ座標は４。
これをｙ＝－ｘ＋２ａに代入して、ｘ＝２ａ－４
Ｐ（２ａ－４、４）
前問より、Ｑ（ａ－１、ａ＋１）

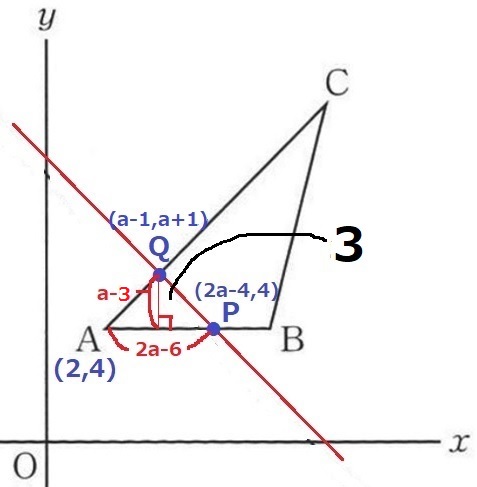
底辺ＡＰの長さ…（２ａ－４）－２＝２ａ－６
高さ…（ａ＋１）－４＝ａ－３
△ＡＰＱの面積は、１/２（２ａ－６）（ａ－３）
＝１/２（２ａ²－12ａ＋18）
＝ａ²－６ａ＋９
＝（ａ－３）²

（１）より△ＡＢＣの面積は24だから、△ＡＰＱは24×１/８＝３
（ａ－３）²＝３
ａ－３＝±√３
ａ＝３±√３
（２）①３≦ａ≦６より、ａ＝３＋√３
*無解答が非常に多かった。

＠余談＠
記述しにくいですけど…最初はこのように解きました。

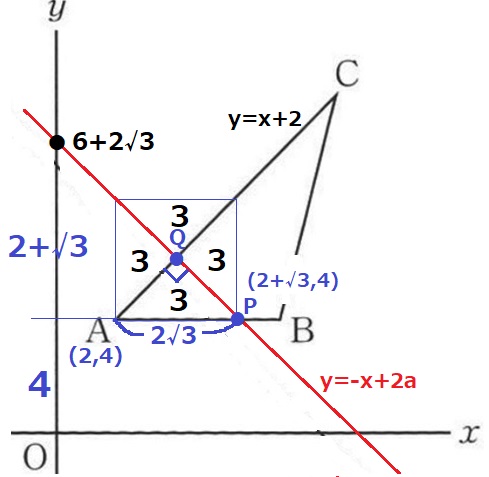
ｙ＝－ｘ＋２ａとＡＣは45°線で直交する。
△ＡＰＱは直角二等辺三角形で、これを４つくっつけると面積が12の正方形になる。
ＡＰ＝√12＝２√３
Ｐのｘ座標は２＋２√３。

ｙ＝－ｘ＋２ａの切片である２ａ＝４＋（２＋２√３）＝６＋２√３
ａ＝３＋√３

大問４（平面図形）－36.9％

（１）　81.7％

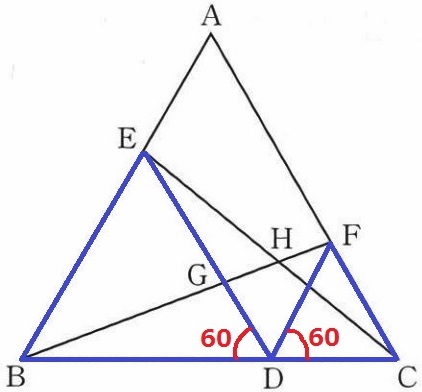
２つの正三角形に注目して、∠ＥＤＦ＝180－60×２＝60°

（２）　56.9％

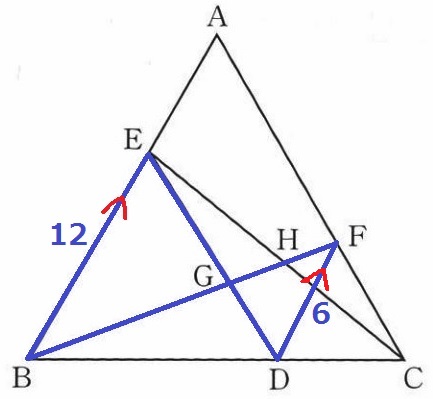
∠ＥＢＤ＝∠ＦＤＣ＝60°で同位角が等しいからＢＥ//ＤＦ
△ＢＥＧ∽△ＦＤＧの相似比より、ＥＧ：ＧＤ＝２：１
*誤答として３：２などが見られた。

（３）　41.0％
△ＢＤＦ≡△ＥＤＣの証明。
問題集によくでてくる形である。

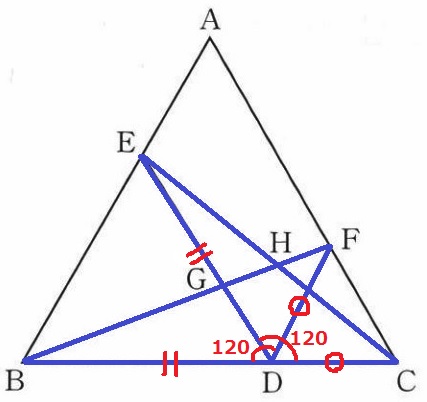
正三角形の１辺より、ＢＤ＝ＥＤ、ＤＦ＝ＤＣ
正三角形の内角と（１）∠ＥＤＦ＝60°から、∠ＢＤＦ＝∠ＥＤＣ＝120°
２辺とあいだの角が等しいので合同。
*誤答では必要な条件を示していないものが見られた。
また、相似条件と合同条件の区別ができていないものもあった。

（４）　14.3％！

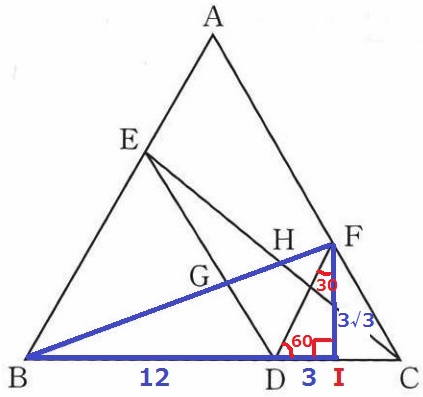
ＢＦを斜辺とする直角三角形をつくる。
Ｆの垂線の足をＩとする。
△ＦＤＣは正三角形なので、これを二等分する△ＦＤＩの内角は30°―60°―90°
辺の比が１：２：√３の直角三角形→ＤＩ＝６÷２＝３ｃｍ、ＦＩ＝３√３ｃｍ
△ＦＢＩで三平方→ＢＦ＝６√７ｃｍ
*無解答も多かった。

（５）　1.1％!!

△ＢＤＧと△ＥＨＧの形が似てるっぽい。
（３）△ＢＤＦ≡△ＥＤＣより対応する角が等しく、
対頂角と合わせると２角相等で、やはり△ＢＤＧ∽△ＥＨＧ
相似比から面積比が求まる。

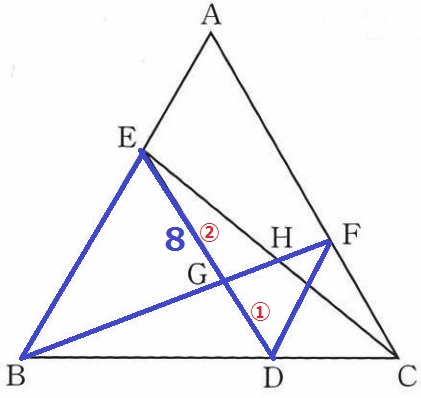
（２）よりＥＧ：ＧＤ＝②：①
ＥＧ＝12×②/③＝８ｃｍ

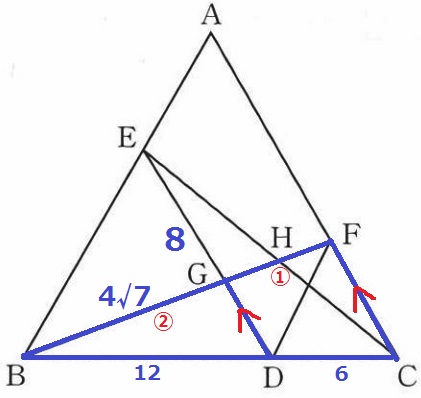
∠ＥＤＢ＝∠ＡＣＢ＝60°で同位角が等しく、ＥＤ//ＡＣ
△ＢＧＤ∽△ＢＦＣより、ＢＧ：ＧＦ＝ＢＤ：ＤＣ＝②：①
（４）よりＢＦ＝６√７ｃｍだから、ＢＧ＝６√７×②/③＝４√７ｃｍ

ＢＧ：ＥＧ＝４√７：８＝√７：２
面積比は相似比の２乗。△ＢＤＧ：△ＥＨＧ＝７：４
△ＢＤＧは△ＥＨＧの７/４倍。
*無解答が非常に多かった。

＠別解＠
つい抜け道を探したくなる(;^ω^)

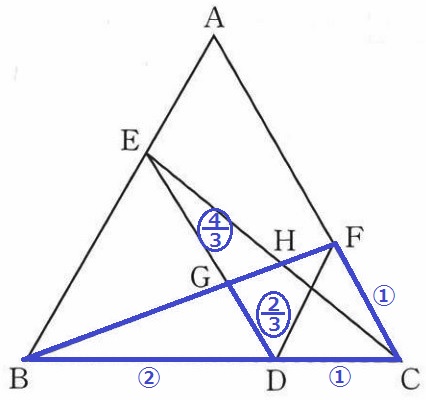
正三角形ＦＤＣの１辺が①、正三角形ＥＢＤの１辺が②。
△ＢＧＤ∽△ＢＦＣより、ＧＤ＝①×２/３＝〇２/３
ＥＧ＝②－〇２/３＝〇４/３

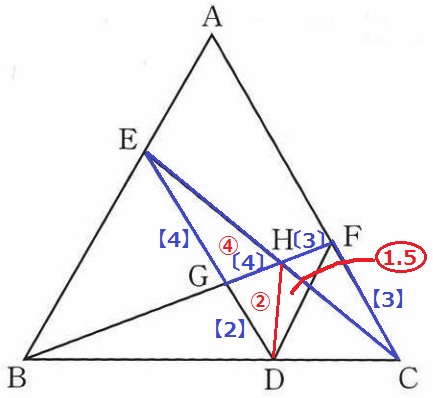
ＥＧ//ＦＣより△ＥＧＨ∽△ＣＦＨ。
相似比はＥＧ：ＣＦ＝４/３：１＝４：３
△ＥＨＧの面積を④とする。
ＨＤに補助線。（２）ＥＧ：ＧＤ＝２：１より△ＤＨＧ＝②
ＧＨ：ＨＦ＝４：３より△ＤＦＨ＝②×３/４＝〇1.5

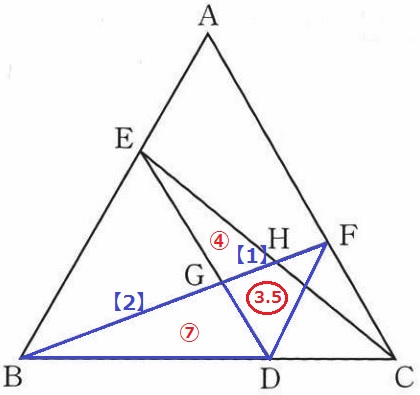
△ＤＧＦ＝②＋〇1.5＝〇3.5
ＢＧ：ＧＦ＝２：１だから、△ＢＤＧ＝〇3.5×２＝⑦
△ＢＤＧ：△ＥＨＧ＝７：４

大問５（整数）－27.0％

（１）　70.9％
【白⇒赤⇒白⇒青】のループ。
13÷４＝３ループ…１
余り１は白。
１ループの長さは１＋３＋１＋５＝10ｃｍなので、
10×３＋１＝31ｃｍ
白色、31ｃｍ

（２）①　18.0％！
ｎは〇枚目。２ｎは偶数枚になる。
【白⇒赤⇒白⇒青】と続くので、〔白→not白→白→not白…〕が互い違いである。
奇数番目にある白の枚数は２ｎ÷２＝ｎ枚

ｎが偶数の場合、２ｎは偶数ｎの２倍だから４の倍数。
２ｎは４の倍数枚→【白⇒赤⇒白⇒青】のループでちょうど終わる（右端は青）
赤と青は１ループに１枚ずつだから同数枚ある。

２ｎ枚のうち、白はｎ枚。
赤と青の合計は、２ｎ－ｎ＝ｎ枚
同数枚なので、赤と青はそれぞれｎ/２枚。

白１ｃｍ、赤３ｃｍ、青５ｃｍなので、
１×ｎ＋３×ｎ/２＋５×ｎ/２
＝ｎ＋（３＋５）×ｎ/２
＝ｎ＋４ｎ＝５ｎ
ア…ｎ、イ…ｎ/２、ウ…ｎ/２、エ…５ｎ
*アは概ねできていたが、完答は少なかった。
規則性を文字を用いて表現することが難しいものと考えられる。

②　1.0％!!
答案では過程も記述する。
ｎが奇数の場合、２ｎはループの途中である赤で終わる（右端が赤）
ということは、赤は青より１枚多い。

白の枚数…ｎ枚

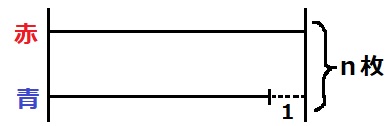
赤の枚数…上のような線分図を描くと見えやすい。
赤と青の和がｎ枚だから、赤は（ｎ＋１）/２枚
青の枚数…（ｎ＋１）/２－１＝（ｎ－１）/２枚

したがって、１×ｎ＋３×（ｎ＋１）/２＋５×（ｎ－１）/２
＝５ｎ－１ｃｍ
*無解答が非常に多かった。