平均44.0点(前年比;-0.4点)
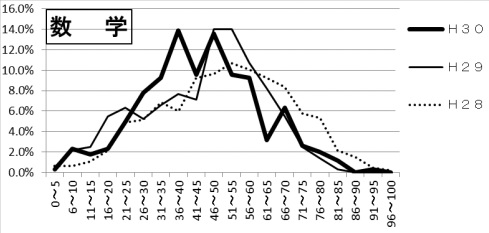
問題はこちら→東進ハイスクールさん(解答)
大問1(計算)
(1) 97.5%
4x+x
=5x
(2) 90.8%
6-4÷(-2)
=6+2
=8
(3) 73.7%
16a2 b÷(-8b)×a
=-2a3
(4) 88.8%
9/√3-2√3
=3√3-2√3
=√3
(5) 86.3%
x2+x-12
=(x-3)(x+4)
(6)連立方程式 82.9%
2x-3y=11・・①
y=x-4 ・・②
②を①に代入。
2x-3(x-4)=11
x=1
②に代入。
y=1-4=-3
x=1 y=-3
(7) 75.4%
因数分解ができないので解の公式
y=(1±√13)/6
(8) 48.5%
yの変域が負であることに注目!
グラフは上に凸 の形。
x=0のとき 最大値:y=0
x=2のとき 最小値:y=-8
(2、8)を通る。
これをy=ax2に代入。
-8=22a
4a=-8 a=-2
(9) 72.5%
イで両辺に+3している。移項です。
(10) 30.3%!
階級値は真ん中の値で計算。
(5×2+15×6+25×7+35×4+45×1)÷20
=460÷20=23m
(11)① 55.7%
小学校の復習。
600×7/100=42g
②正答―19.0%! 一部正答―7.6% 無答―39.8%
ありがたいことに表が提供されている。
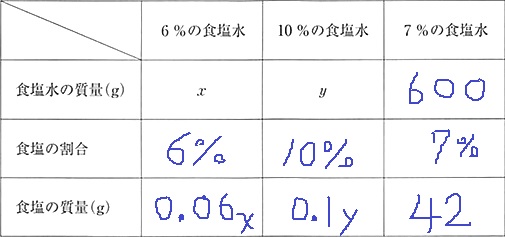
↑表がなくても、自分で書いて情報整理できるように!
1行目と3行目で連立
x+y=600
0.06x+0.1y=42
これを解いて、6%の食塩水・・450g 10%の食塩水・・150g

@別解@
本問は連立方程式で使えませんが、中学入試にでてくる天秤法だと楽。
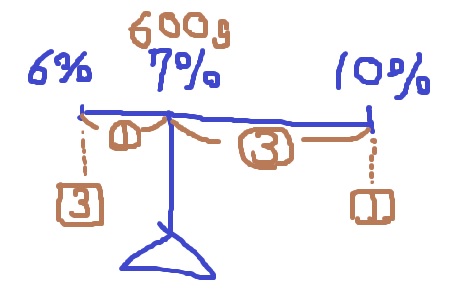
6%と10%を混ぜ、7%にする。支点を7%に天秤を作る。
支点からの距離は、1:3
左右を釣り合わせるには、重りを3:1にする。
600gを3:1に分けると、450gと150gになりますね。
大問2(小問集合)
(1)確率 14.8%!
『abの積の約数が3個以上』は数が多いので、
指針は”全体-〔約数が2個以下〕”
約数が2個しかない→素数
また、1は素数ではないが、1の約数は1個なので(1、1)も満たす。
(a、b)=(1、1)(1、2)(2、1)(1、3)(3、1)(1、5)(5、1)
計7通り
約数が3個以上は、36-7=29個
29/36
(2)正八面体の体積 28.3%!
底面積は正方形BCDE
その面積は対角線×対角線×1/2
BD&CE(対角線)=6cm
高さは上下で3cmずつだが、上下一体に考えて6cmとしてしまおう。
6×6×1/2×6×1/3=36cm3
(3)作図 5.3%!! 一部正答―2.0% 無答―19.3%
まず、折ったあとにAがBCに移る点A’を考える。
Pに針を合わせ、AからBC方向にシュッと弧を描く。その交点がA’
AA’の垂直二等分線で終了。
折り目を対称の軸とした線対称ですね。
(4)証明 21.8%! 一部正答―22.1% 無答―28.6%
補助線をひいて、2つの三角形が相似であることを指摘。
補助線は〔AB・DC〕パターン、〔AD・BC〕パターンのどちらでもOK。
円周角の定理と対頂角から2角が等しい → ∽
図形が円で囲まれていたら、円周角の定理を疑おう。
@方べきの定理@
PA:PD=PB:PCで、内項と外項の積から、
PA・PC=PB・PDとなる。
これを方べきの定理という。使える定理なので覚えておきたい。
大問3(規則)
(1)72.0% 一部正答―8.7% 無答―1.7%
7だから、やっちゃった方がいい。
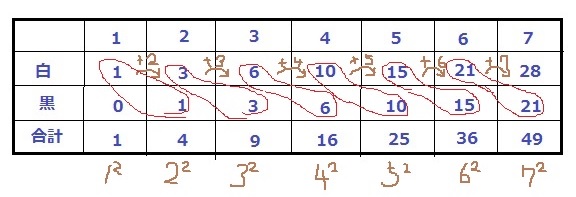
白は、+2、+3、+4、+5・・
黒は、0からスタートし、1コ前の白。
合計は、n番目の2乗(n2)
ア・・28 イ・・21
(2) 2.5%!!
上の規則から、黒の枚数を一般化する。
合計はn2
白はn番目までの総和なので、1/2n(n+1)
黒の枚数a=n2-1/2n(n+1)=n2-(n2+n)/2=(n2-n)/2
@別解@
白が1/2n(n+1)で、黒は白より1コ遅れるわけなので、
1/2n(n+1)のnを(n-1)に置き換えればいい。
1/2(n-1){(n-1)+1}=(n2-n)/2
@公式で紹介された解答例@
黒の枚数がa枚なので、aで白の枚数を表してみる。
黒のタイルの上には、対になるように白のタイルがくる。
n番目のnは最下段の白のタイルの枚数(●)と同じなので、
nに黒の枚数の総和(●)を足せば白の枚数となる。
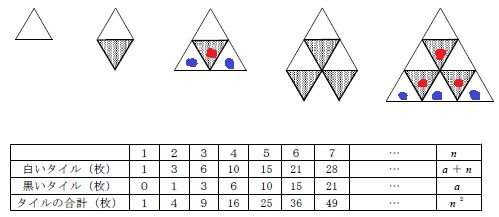
(a+n)+a=n2
2a+n=n2
これをaについて解く。
大問4(関数)
(1) 38.4%
y=1/2x2から
A(-2、2) B(3、9/2)
この2点を通る一次関数(y=ax+b)を求める。
連立で解いて、y=1/2x+3
(2) 2.0%!! 一部正答―4.5% 無答―70.3%!
説明問題
AC:CE=1:3からC座標
C座標かがy=ax2に放り込み、aを求める。
a=1
(3) 0.3%!!!
FGに補助線。
四角形CDGFの求積なので、C・D・G・Fの4点の座標を求める。
前問から、C(-3/2、9/4)
y=x2とℓ:y=1/2x+3との交点から、D(2、4)
OD:y=2xとy=1/2x2との交点G(4、8)
OC:y=-3/2xとy=1/2x2の交点F(-3、9/4)
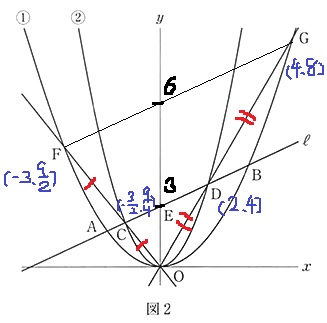
↑ここまで出すのに一苦労(;´д`)
処理手順が多い。素早くかつミスなく行いたい。
なんかℓとFGが平行っぽくみえる。
実は、FG=1/2x+6となり、FG//ℓ
△ODC:△OGF=1:4
四角形CDGFは△OGFの1/4
△OGFはおなじみの等積変形。
△OGF=(4+3)×6÷2=21
四角形CDGF=21×3/4=63/4cm 2



コメント